Tutorial is loading...
(Developing — vintage_Vlad_Makeev, ch_egor, V--o_o--V, demon1999)
Tutorial is loading...
(Developing — ch_egor)
Tutorial is loading...
(Developing — ch_egor)
Tutorial is loading...
(Developing — halin.george)
Tutorial is loading...
(Developing — Sehnsucht)
Tutorial is loading...











Thanks for the editorial !
For Problem F,cant we make p = sqrt(n) and get the complexity as n*root(n)?
Or did I misunderstood something?
Complexity is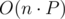 for movement of
for movement of  ,
,  and
and 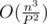 for movement of
for movement of  . If you choose
. If you choose 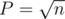 you got
you got 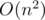 .
.
My bad
Thanks for the reply
I'm having trouble understanding how those complexities are derived. Can you explain it in more detail? Thanks!
Edit: figured it out.
There are O(N^2/P^2) blocks, each with O(P^2/N) elements.
Left pointer: For each block with O(P^2/N) elements, it takes O(P) to go from one element to the next. So the complexity for processing each block is O(P^3/N), and the complexity of processing every block is O(P^3/N) * O(N^2/P^2) = O(NP).
Right pointer: For each of O(N^2/P^2) blocks, the right pointer moves O(N) times. The total number of times the right pointer moves is O(N^3/P^2).
We can find the minimum complexity by setting the left and right pointers complexity equal. So NP = N^3/P^2, which gives P = N^(2/3). So the total complexity for both movements is O(N^(5/3)).
plz explain
n>=k part in problem c
extract prefix of length k and find the next string lexicographically.
In 5th problem it should be multiset and not set as there could be equal values.
can someone tell me problem in this 35727835 __ __fixed now
gotem. boyz
debug urself
The explanation for D kinda seems more complicated than it needs to be. I mean... the problem gives you three cases.
First case allows you to change a 1 to a 0 if some condition happens. Second case allows you to change a 0 to a 1 if some condition happens. Third case allows you to keep the current digit (with no condition).
Therefore, to solve, if the current digit was changed from a 1 to a 0, apply the restrictions for case 1; if it was changed from a 0 to a 1, apply restrictions for case 2. Else, no restrictions need to be applied.
All cases here are just for prove that we haven't other cases. It's obvious that we don't need upper bound for and lower bound for
and lower bound for  .
.
For multiset in E do we maintain a rolling sum. When inserting in multiset we add it to that sum and while removing ( if the size of multiset exceeds the required (i-j+1)/c elements ) we subtract. And final is sum of i-j+1 elements minus the rolling sum we maintained? Or we have to do something else?
I don't get why you even need a rolling sum
'storing sum of minimums in some structure like std::multiset.'
I did not understand this line in the editorial.
So i also struggled with this line for some time. And here is what i figured:
you'll need four things: a tree-multiset (multiset< int > ms), an integer containing sum (int sum), an integer with the greatest element in the multiset to be contained in the sum (the greatest summant; int geis) and an integer counting summants equal to geis in the sum (int nog).
Firstly we set: ms = empty multiset, sum = geis = nog = 0; Only when ms.size() == c we reassign sum and geis with the first smallest number in ms: sum = geis = *(ms.begin()); nog = 1;
Now, when you insert an element (int el) to ms you need to update sum and geis values only when ms.size() > c.
Please note, that each update requires O(1) searches (or other operations with the same complexity) in a tree-multiset of size O(n), thus requiring O(log n) time for each insert, O(n log n) time for each i in the main for loop and finally O(n**2 log n) for the solution.
For problem F: sorry, I don't understand why we should change t to one in O(1) time. And does it means that we should let r be the sequence of {r1, r1 + s, r1 + 2s, ...}(s = n2 / P2) and let l and t be different number in n as step of P so there may be O(n5 / 3 × n2 / 3) different movement.
I think it's supposed to say that you can change t by one in O(1) time, i.e. go from t to t + 1 or t - 1 as necessary. What you do is sort the queries as described and answer them using Mo's Algorithm.
In editorial of F, how it's ensured after sorting that 1st type queries are calculated after the intended number of 2nd type queries for ex. lets say P = 10 so for number of change queries from 1 to 9 will fall together and there might be wrong ordering in processing them.
Anyone have any idea why Problem D is tagged as Binary Search / Implementation? It seems more like a Greedy solution to me.
You can binary search for l and r. The idea is simple: just check if the conditions are satisfied at the points where we have "00001" or "11110" (because these are the ones which matter) for l and r separately (while doing the binary search). Since the answer is guaranteed to exist, you can find it by binary search too.