NAIPC is coming up on March 24th (start time here). More information about the contest can be found on this page. More information on how to register can be found on this page. You can register in teams of up to 3. This contest will be on Kattis.
Several hours later, it will be available as an open cup round as the Grand Prix of America (start time here). Please only participate in one of them, and don't discuss problems here until after the open cup round has ended.
The deadline to register for the contest on Kattis is March 21st. You will need an ICPC account to register (you can see instructions in the link above on how to create one if needed).
You can see some past years' problems here: 2017, 2016
UPD 1: The deadline to register your team is soon.
UPD 2: Contests are over
- NAIPC standings: https://naipc18.kattis.com/standings
- open cup standings: http://opentrains.snarknews.info/~ejudge/res/res10416
- solutions and test data: http://serjudging.vanb.org/?p=1165











G seems to be a problem related to matroid intersection.
How to solve it?
Edit : I figure out how to solve it after reading the author's solution.
Dual matroid, and remove edges one by one.
How to solve B and J ?
B: "Degree sequences" is a big hint.
This problem is also (almost) an old POI problem: https://main.edu.pl/en/archive/oi/18/kon
J: The graph must be a cactus for possible solutions. Then it's a DP problem on a cactus.
I: I had to optimize my O(NM) solution (and still it takes 1.8s). Is there something faster?
You can speed up to N+M**2 if you can multiply polynomial by constant in O(1).
I wasted 90min in problem I and still cannot solve :(
Here is O(NM) solition, which doesn't seems too optimized for me, and works for 0.5s
C ?
Do operations in reverse. Then i-th operation xors segment of length i.
How to solve after that ?
Do the bitmask dp. dpi, msk is 1 iff after i operations we can get the mask msk. The answer is not more than n, so it works in O(2nn2).
As I see, author solution on F is O(n+m). Problem can be solved in O(log^3) (or probably, log^2). The idea is follwing. We can find a number of points below passing through point (x, y) in O(logn) time. This can be done by Euclid-like approach.
We want to find a first direction (i.e irreducibly p, q), such that number of point below p/q is less then number we need. To do that, we can go down by Stern–Brocot tree
Formally, that means that we have (p1/q1 which is lower bound for our direction, and p2/q2 to upper bound). Initially, 0/1 and 1/0 are them. If (p1+p2)/(q1+q2) is too far, p1/q1 is answer, because there is no numbers between them. If not, we can change one of bounds to it. Although we have linear number of steps, we have O(logn) number of "turns", that is positions, where we change different bound with previous one. Number of steps before next turn, can be found using binary search. If do so, O(log^2) times of solving "points under line" problem needed.
Code here is a bit messy, because i was rewring linear searches of turns to binary on last minutes, but solves problem in 9ms.
Instead of Stern-Brocot tree, we binary searched on doubles, and used chain fraction to find the closest p/q with q<=n. This is log**2 I think.
If you use normal binary searches, the runtime is Θ(log3). If you use exponential search instead, the runtime drops to Θ(log2). (Exponential search runs in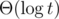 where t is the number steps you end up taking.)
where t is the number steps you end up taking.)
During the contest I just improved the constant of the linear searches by trying steps of 1000 first.