Long time no see!
As VK Cup Round 2 and its two parallel rounds (Div. 1 and Div. 2) comes to a close, we're here to congratulate on all who did well on the contest and cheer for everyone who participated — the queue won't stop you!
Here are the detailed tutorials for the problems. Feel free to discuss in the comments!
Kudos to arsor for translating the tutorials into Russian!
Tutorial is loading...
Model solution
_, s = input(), input()
print('Yes' if
('??' in s or 'C?C' in s or 'M?M' in s or 'Y?Y' in s or s[0] == '?' or s[-1] == '?') and
not ('CC' in s or 'MM' in s or 'YY' in s)
else 'No')
Alternative solution (Errichto)
#include <bits/stdc++.h>
using namespace std;
void NO() {
puts("No");
exit(0);
}
void YES() {
puts("Yes");
exit(0);
}
int main() {
int n;
cin >> n;
string s;
cin >> s;
for(int i = 0; i < n - 1; ++i)
if(s[i] != '?' && s[i] == s[i+1])
NO();
for(int i = 0; i < n; ++i) if(s[i] == '?') {
if(i == 0 || i == n - 1) YES();
if(s[i+1] == '?') YES();
if(s[i-1] == s[i+1]) YES();
}
NO();
}
(by cyand1317)
Tutorial is loading...
Model solution
#include <cstdio>
typedef long long int64;
static const int MAXN = 53;
static int n, m;
static bool a[MAXN][MAXN];
static int64 b[MAXN];
int main()
{
scanf("%d%d", &n, &m); getchar();
for (int i = 0; i < n; ++i)
for (int j = 0; j <= m; ++j) a[i][j] = (getchar() == '#');
for (int i = 0; i < n - 1; ++i)
for (int j = i + 1; j < n; ++j) {
bool all_same = true, no_intersect = true;
for (int k = 0; k < m; ++k) {
if (a[i][k] != a[j][k]) all_same = false;
if (a[i][k] && a[j][k]) no_intersect = false;
}
if (!all_same && !no_intersect) {
puts("No"); return 0;
}
}
puts("Yes"); return 0;
}
Alternative solution with DSU in O(nm alpha(n)) (skywalkert)
#include <bits/stdc++.h>
using namespace std;
const int maxn = 5001, maxm = maxn << 1 | 1;
int n, m, dsu[maxm], cB[maxm], cW[maxm], cE[maxm];
char buf[maxn];
int dsu_find(int u) {
return dsu[u] < 0 ? u : (dsu[u] = dsu_find(dsu[u]));
}
void dsu_merge(int u, int v) {
u = dsu_find(u);
v = dsu_find(v);
if(u == v) {
++cE[u];
return;
}
if(dsu[u] < dsu[v])
swap(u, v);
dsu[v] -= dsu[u] == dsu[v];
dsu[u] = v;
cB[v] += cB[u];
cW[v] += cW[u];
cE[v] += cE[u] + 1;
}
int main() {
scanf("%d%d", &n, &m);
memset(dsu, -1, (n + m) * sizeof(int));
for(int i = 0; i < n; ++i)
cB[i] = 1;
for(int i = 0; i < m; ++i)
cW[n + i] = 1;
for(int i = 0; i < n; ++i) {
scanf("%s", buf);
for(int j = 0; j < m; ++j)
if(buf[j] != '.')
dsu_merge(i, n + j);
}
for(int i = 0; i < n + m; ++i)
if(dsu_find(i) == i && cB[i] * cW[i] != cE[i]) {
puts("No");
return 0;
}
puts("Yes");
return 0;
}
Alternative solution in O(nm)
#include <cstdio>
#include <algorithm>
#include <vector>
static const int MAXN = 1004;
static int n, m;
static bool g[MAXN][MAXN];
// c[i] = set of rows where the i-th column is coloured
static std::vector<int> c[MAXN];
static bool checked[MAXN] = { false };
int main()
{
scanf("%d%d", &n, &m); getchar();
for (int i = 0; i < n; ++i)
for (int j = 0; j <= m; ++j) {
g[i][j] = (getchar() == '#');
if (g[i][j]) c[j].push_back(i);
}
for (int i = 0; i < n; ++i) if (!checked[i]) {
std::vector<int> r;
for (int j = 0; j < m; ++j) if (g[i][j])
for (int k : c[j]) r.push_back(k);
std::sort(r.begin(), r.end());
r.resize(std::unique(r.begin(), r.end()) - r.begin());
for (int k : r) {
if (checked[k]) { puts("No"); return 0; }
checked[k] = true;
for (int p = 0; p < m; ++p)
if (g[i][p] != g[k][p]) { puts("No"); return 0; }
}
}
puts("Yes"); return 0;
}
(by cyand1317)
Tutorial is loading...
Model solution
#include <iostream>
#include <sstream>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
#include <string>
#include <cstring>
#include <cassert>
#include <iomanip>
#include <algorithm>
#include <set>
#include <map>
#include <ctime>
#include <cmath>
#define forn(i, n) for(int i=0;i<n;++i)
#define fore(i, l, r) for(int i = int(l); i <= int(r); ++i)
#define sz(v) int(v.size())
#define all(v) v.begin(), v.end()
#define pb push_back
#define mp make_pair
#define x first
#define y1 ________y1
#define y second
#define ft first
#define sc second
#define pt pair<int, int>
template<typename X> inline X abs(const X& a) { return a < 0? -a: a; }
template<typename X> inline X sqr(const X& a) { return a * a; }
typedef long long li;
typedef long double ld;
using namespace std;
const int INF = 1000 * 1000 * 1000;
const ld EPS = 1e-9;
const ld PI = acos(-1.0);
const int N = 100 * 1000 + 13;
int n, u;
int a[N];
int idx1 = -1, idx2, idx3;
inline void read() {
scanf("%d%d", &n, &u);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
}
inline void solve() {
int k = 0;
for (int i = 0; i < n; i++) {
k = max(k, i);
while (k + 1 < n && a[k + 1] - a[i] <= u) {
k++;
}
if (k - i - 1 <= 0) {
continue;
}
int j = i + 1;
if (idx1 == -1 || (a[k] - a[j]) * 1ll * (a[idx3] - a[idx1]) > (a[idx3] - a[idx2]) * 1ll * (a[k] - a[i])) {
idx1 = i, idx2 = j, idx3 = k;
}
}
if (idx1 == -1) {
cout << -1 << endl;
return;
}
cout.precision(20);
cout << (double)(a[idx3] - a[idx2]) / (a[idx3] - a[idx1]) << endl;
}
int main () {
#ifdef fcspartakm
freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
srand(time(NULL));
cerr << setprecision(10) << fixed;
read();
solve();
//cerr << "TIME: " << clock() << endl;
}
(by KAN, prepared by fcspartakm)
Tutorial is loading...
Model solution
#include <cstdio>
#include <algorithm>
typedef long long int64;
static const int MAXN = 1e5 + 4;
static int n, m[MAXN];
static int t[MAXN];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; ++i) scanf("%d", &m[i]);
for (int i = n - 1, cur = 0; i >= 0; --i) {
cur = std::max(0, cur - 1);
cur = std::max(cur, m[i] + 1);
t[i] = cur;
}
int64 ans = 0;
for (int i = 0, cur = 0; i < n; ++i) {
cur = std::max(cur, t[i]);
ans += cur;
}
for (int i = 0; i < n; ++i) ans -= (m[i] + 1);
printf("%lld\n", ans);
return 0;
}
(by cyand1317)
Tutorial is loading...
Model solution
#include <cstdio>
#include <algorithm>
#include <utility>
typedef long long int64;
static const int MAXN = 1e5 + 4;
static const int MAXX = 1e8 + 4;
static int n, w;
static int x[MAXN], v[MAXN];
struct fraction {
template <typename T> static inline T gcd(const T a, const T b) {
return (b == 0) ? a : gcd(b, a % b);
}
int64 num, deno;
inline void simplify() {
if (deno < 0) { num *= -1; deno *= -1; }
int64 g = gcd(num < 0 ? -num : num, deno); num /= g; deno /= g;
}
fraction() { }
fraction(int64 num, int64 deno) : num(num), deno(deno) { simplify(); }
inline bool operator < (const fraction &rhs) const {
return num * rhs.deno < deno * rhs.num;
}
inline bool operator != (const fraction &rhs) const {
return num * rhs.deno != deno * rhs.num;
}
};
// Time bounds at which clouds can arrive at the origin
static std::pair<fraction, fraction> t[MAXN];
// Used at discretization
static std::pair<fraction, int> d[MAXN];
static int p[MAXN];
struct bit {
static const int MAXN = ::MAXN;
int f[MAXN];
bit() { std::fill(f, f + MAXN, 0); }
inline void add(int pos, int inc) {
for (++pos; pos < MAXN; pos += (pos & -pos)) f[pos] += inc;
}
inline int sum(int rg) {
int ans = 0;
for (++rg; rg; rg -= (rg & -rg)) ans += f[rg];
return ans;
}
inline int sum(int lf, int rg) {
return sum(rg) - sum(lf - 1);
}
} arkady;
int main()
{
scanf("%d%d", &n, &w);
for (int i = 0; i < n; ++i) scanf("%d%d", &x[i], &v[i]);
for (int i = 0; i < n; ++i) {
int64 v1 = v[i] - w, v2 = v[i] + w;
t[i] = {fraction(-x[i], v1), fraction(-x[i], v2)};
}
for (int i = 0; i < n; ++i) t[i].second.num *= -1;
std::sort(t, t + n);
for (int i = 0; i < n; ++i) t[i].second.num *= -1;
for (int i = 0; i < n; ++i) d[i] = {t[i].second, i};
std::sort(d, d + n);
for (int i = 0, rk = -1; i < n; ++i) {
if (i == 0 || d[i].first != d[i - 1].first) ++rk;
p[d[i].second] = rk;
}
/*for (int i = 0; i < n; ++i)
printf("%.4lf %.4lf | %d\n",
(double)t[i].first.num / t[i].first.deno,
(double)t[i].second.num / t[i].second.deno, p[i]);*/
int64 ans = 0;
for (int i = 0; i < n; ++i) {
ans += arkady.sum(p[i], MAXN - 1);
arkady.add(p[i], 1);
}
printf("%lld\n", ans);
return 0;
}
(by KAN, prepared by cyand1317)
Tutorial is loading...
Model solution
/**
* This is a solution for problem wardrobe
* This is nk_ok.cpp
*
* @author: Nikolay Kalinin
* @date: Tue, 20 Mar 2018 21:48:33 +0300
*/
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
using D = double;
using uint = unsigned int;
template<typename T>
using pair2 = pair<T, T>;
#ifdef WIN32
#define LLD "%I64d"
#else
#define LLD "%lld"
#endif
#define pb push_back
#define mp make_pair
#define all(x) (x).begin(),(x).end()
#define fi first
#define se second
struct tbox
{
int h, t;
};
inline bool operator<(const tbox &a, const tbox &b)
{
if (a.t != b.t) return a.t < b.t;
return a.h > b.h;
}
const int maxn = 10005;
const int inf = 1e9;
tbox b[maxn];
int ans[maxn];
int n, l, r;
int main()
{
scanf("%d%d%d", &n, &l, &r);
int sumh = 0;
for (int i = 0; i < n; i++)
{
scanf("%d", &b[i].h);
sumh += b[i].h;
}
tie(l, r) = pair{sumh - r, sumh - l};
for (int i = 0; i < n; i++) scanf("%d", &b[i].t);
sort(b, b + n);
for (int i = 0; i <= sumh; i++) ans[i] = -inf;
ans[0] = 0;
for (int i = 0; i < n; i++)
{
for (int h = sumh - b[i].h; h >= 0; h--) ans[h + b[i].h] = max(ans[h + b[i].h], ans[h] + b[i].t * (h + b[i].h >= l && h + b[i].h <= r));
}
cout << *max_element(ans, ans + sumh + 1) << endl;
return 0;
}
(by KAN)
Tutorial is loading...
Model solution
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxd = 10, maxl = 18, maxs = 81, BLEN = 5, BMSK = 31;
struct States {
vector<LL> keys, vals[maxd + 1];
void insert(LL key) {
keys.push_back(key);
}
void initialize(LL val = 0) {
sort(keys.begin(), keys.end());
keys.erase(unique(keys.begin(), keys.end()), keys.end());
for(int i = 0; i < maxd; ++i)
vals[i].assign(keys.size(), val);
}
void summation() {
for(int i = 1; i < maxd; ++i)
for(vector<LL>::iterator it = vals[i - 1].begin(), jt = vals[i].begin(); jt != vals[i].end(); ++it, ++jt)
*jt += *it;
}
size_t size() const {
return keys.size();
}
void update(int upp, LL key, LL adt) {
vals[upp][lower_bound(keys.begin(), keys.end(), key) - keys.begin()] += adt;
}
LL find(int upp, LL key) {
vector<LL>::iterator it = lower_bound(keys.begin(), keys.end(), key);
if(it == keys.end() || *it != key)
return 0;
return vals[upp][it - keys.begin()];
}
} f[maxd + 1][maxl + 1];
LL c[2][maxl + 1], bit[maxd + 1];
bitset<maxs + 1> vis[maxd + 1];
void dfs(int dep, int cnt, int sum, LL msk) {
if(dep == maxd) {
for(int i = sum >> 1; i >= 0; --i)
if(vis[dep - 1].test(i)) {
int dif = sum - i - i;
if(dif > 1)
f[dif][0].insert(msk);
break;
}
return;
}
vis[dep] = vis[dep - 1];
dfs(dep + 1, cnt, sum, msk);
while(cnt < maxl) {
vis[dep] |= vis[dep] << dep;
dfs(dep + 1, ++cnt, sum += dep, msk += bit[dep]);
}
}
LL solve(int dif, LL lim) {
char dig[maxl + 3];
int len = sprintf(dig, "%lld", lim);
LL ret = 0, msk = 0;
States *F = f[dif];
for(int i = 0; i < len; ++i) {
dig[i] -= '0';
if(len - i > maxl) {
for(int j = 0; j < dig[i]; ++j)
ret += F[len - i - 1].find(maxd - 1, msk);
} else if(dig[i]) {
ret += F[len - i].find(dig[i] - 1, msk);
msk += bit[dig[i]];
}
}
return ret;
}
LL solve2(LL lim) {
char dig[maxl + 3];
int len = sprintf(dig, "%lld", lim), part = 0;
LL ret = 0;
for(int i = 0; i < len; ++i) {
dig[i] -= '0';
int odd = dig[i] >> 1, even = (dig[i] + 1) >> 1;
ret += c[part][len - 1 - i] * odd + c[part ^ 1][len - 1 - i] * even;
part ^= dig[i] & 1;
}
return ret;
}
int main() {
c[0][0] = 1;
for(int i = 0; i < maxl; ++i) {
int odd = maxd >> 1, even = (maxd + 1) >> 1;
c[0][i + 1] = c[0][i] * even + c[1][i] * odd;
c[1][i + 1] = c[0][i] * odd + c[1][i] * even;
}
bit[1] = 1;
for(int i = 2; i < maxd; ++i)
bit[i] = bit[i - 1] << BLEN;
vis[0].set(0);
dfs(1, 0, 0, 0);
for(int i = 2; i < maxd; ++i) {
f[i][0].initialize(1);
for(int j = 0; j < maxl; ++j) {
States &cur = f[i][j], &nxt = f[i][j + 1];
for(int idx = 0, sz = cur.size(); idx < sz; ++idx) {
int cnt = j;
LL msk = cur.keys[idx], tmp = msk;
for(int k = 1; k < maxd; ++k, tmp >>= BLEN) {
int rem = tmp & BMSK;
if(!rem)
continue;
cnt += rem;
nxt.insert(msk - bit[k]);
}
if(cnt < maxl)
nxt.insert(msk);
}
nxt.initialize(0);
for(int idx = 0, sz = cur.size(); idx < sz; ++idx) {
int cnt = j;
LL msk = cur.keys[idx], ways = cur.vals[maxd - 1][idx], tmp = msk;
for(int k = 1; k < maxd; ++k, tmp >>= BLEN) {
int rem = tmp & BMSK;
if(!rem)
continue;
cnt += rem;
nxt.update(k, msk - bit[k], ways);
}
if(cnt < maxl)
nxt.update(0, msk, ways);
}
nxt.summation();
}
}
int t;
scanf("%d", &t);
for(int Case = 1; Case <= t; ++Case) {
LL L, R;
int k;
scanf("%lld%lld%d", &L, &R, &k);
LL ans = R + 1 - L;
if(!k) {
ans -= solve2(R + 1) - solve2(L);
for(int i = 2; i < maxd; i += 2)
ans -= solve(i, R + 1) - solve(i, L);
} else {
for(int i = k + 1; i < maxd; ++i)
ans -= solve(i, R + 1) - solve(i, L);
}
printf("%lld\n", ans);
}
return 0;
}
(by Claris and skywalkert)
My gratitude to the coordinators, problem authors, testers, and every participant. You made all this possible! Cheers \(^ ^)/











Auto comment: topic has been updated by cyand1317 (previous revision, new revision, compare).
funny python fact: in 956B NlogN solution in Python3 is very likely to get TLE. For the pretests, I got AC with 950ms out of 1000. I fixed it by switching to PyPy, and of course another option was to optimize the solution to O(N)
good! your solution quite nice and helpful, learned a lot!!!
agree!
Hi, can some author pls check this my same solution got tle in contest and passes outside. TLE:- http://codeforces.com/contest/956/submission/36596404 AC:- http://codeforces.com/contest/956/submission/36601475
Submissions to problems are not yet enabled. How did you submit the solution after contest?
I don't know about other problems but submissions for div1 d is enabled.
div2 E(div1 D) "That leaves us only with a binary indexed tree to be implemented." How to use a binary indexed tree to solve the problem "Inversion pairs".
The only way I can find out to solve this is using set or balanced binary search tree.
Someone plz tell me about how to do it.
Each plane can be represented as a line segment from (-w, a[i]) to (w, b[i]). So a pair (i, j) of 2 planes is counted if two segments are intersected. i.e. a[i] <= a[j] && b[i] >= b[j] W.L.G: a[1] <= a[2] <= ... <= a[n]. For each i from 1 to n, count the sum of values in [bi, ∞], then increase the value at b[i] by 1.
"For each i from 1 to n, count the sum of value in [bi, ∞], then increase value at b[i] by 1." Yes, this is a clear way to do that. It is just like the way I found out by using set before. My way is just using a set, with inserting b[i] like your "increase value at b[i] by 1", and calculate the counts like your "count the sum of value in [bi, ∞]". Thank you.
I spent a very little time and found out I can count the intersections of the set "segment((v+w)/x,(v-w)/x)", and I can't implemented it correctly and completely within a half our.
I used about 25min, thinking about 2-pointers to solve this, and at last was some how convinced I should use some data-structure, and there was just 5min left.
I understand how number of inversions can be counted with BIT. But how two different type of planes which are (left to right plane) and (right to left plane) could be treated in the same time even though -w decreases speed of left to right plane but increases speed of right to left plane?
In the tutorial of DIV-2D: In order to satisfy later days, ti ≥ tj - (j - i) should hold for all j > i. What does it mean by this line?
On each day we can increase t by at most one, thus ti ≥ ti + 1 - 1, which is equivalent to the condition that ti ≥ tj - (j - i) holds for all j > i.
The tutorial will be updated soon, thanks for pointing out.
What's the best solution jury has for E? I think my solution can be optimized into S sqrt S (where S is sum of values, of course), and it's not significantly harder than S^2
What was the reason of such a small S?
We know the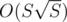 solution, but we thought it was not interesting to accept only such solutions, the main idea is how to do the knapsack, not how to optimize it.
solution, but we thought it was not interesting to accept only such solutions, the main idea is how to do the knapsack, not how to optimize it.
Anyone can explain or provide relevant link for the sqrt optimization of knapsack?
Thanks
You can check out the solution for problem "Polandball and gifts" described here:
http://codeforces.com/blog/entry/49793
Can someone please tell me what's wrong with my code for Div2C? It is failing test #9. :( 36602743 Instead of using upper_bound to search for k (like everyone else did), I did lower_bound to search for i. According to me, it should give the same result, and I can't find my mistake. Please help! Thanks!
Actually, it's not the same.
For sample input:
4 6
3 5 6 9
Answer should be: 0.75 — Triple (5, 6, 9)
Your output: 0.66667 — Triple (3, 5, 9)
My solution for E:
it's clear that the bottoms of important boxes from the answer should form a subinterval [l, r] of [L, R] and their order doesn't matter; we need to put some boxes with sum of heights ≥ L and ≤ R - (r - l) below them
let's suppose that x boxes lie completely within [l, r]; if we don't need to use all remaining important boxes to get them high enough, the answer is at least x + 1; either way, it's at least x
these x boxes should be the smallest x important boxes; proof: if there's an important box a and a smaller unused important box b, we can replace a by b and decrease r; if there's a smaller important box b used below height l, we can swap a and b, which doesn't change r and increases l, creating another valid solution
thanks to this observation, let's use a fast enough DP to find all heights ≤ R reachable only using unimportant boxes; then, we can keep adding to them important boxes in the reverse order of heights and before adding each of them, find the smallest possible l (that can be constructed using boxes added so far as a subset sum) and binsearch for the maximum number of important boxes that haven't been added to the subset sum candidates yet and have height ≤ R - l
now we've got the maximum possible x (as defined above); the answer could be x + 1, but only if we construct it using these x smallest important boxes
let's find all subset sums of the remaining important boxes, remove the sum corresponding to their full set and add all unimportant boxes; if we can construct a height ≥ L and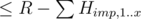 , the answer is x + 1
, the answer is x + 1
Here, "fast enough DP" is the classic O(RN) DP for subset sums implemented using bitsets, which give us a massive speedup, something like O(RN / 64). My code runs in 30 ms.
It's not hard to solve 956 A in O(n·m).Make a bipartite graph with rows and columns where row and column are connected if in there intersection there is #.Now just do Dfs on components and then check if in intersection of every row R and column C in component there is #.
It's a bit advanced for problem A; we've tested it during preparation, though.
There is an easier solution with O(n*m) complexity. You can just make array, f[i] — first row such that a[f[i]][i] = '#'. Now for each row iterate over columns and if there is more than one distinct f[i] for this row, answer is no. There are some other simple cases, just look this code: 36581433
please help me debug this Div 2-C code. I can't figure where the mistake is
You're moving the two pointers i,k in the wrong order : what you're doing is for all k increase i until (i,i+1,k) is valid, then move onto k+1. But it's possible that increasing i further for the same i yields a better result : try "4 1000 1 100 101 200" You need to increase i one by one, and for each i it's true that the largest possible k (as long as e[k]-e[i]<=u) gives the best possible answer for this i.
I didn't understand Div2 D solution at all. Can someone please explain elaborately?
My solution for D passed pretests but failed same test case in system testing (TLE) . How is that possible?? http://codeforces.com/contest/956/submission/36599452 Also i think my solution is nlogn so there should not be any problem with time? Can anyone help?
don't use map. It's too slow.
I think the problem was with long double. I was reading values directly in long double variables. Instead if i read them as int and then initialize my long double variables with integer than it takes considerably less time. http://codeforces.com/contest/956/submission/36609647
happened to me once
Alternate solution for 956C - Речная загадка:
First, note that d[i] = d[i-1] + m[i-1] – m[i] + (0 or 1). The only condition is that d[i] >= 0. For each day from 2 to n, greedily "choose" +0. Now at some day i in the future, maybe d[i] turns out to be negative. In this case, we need to go back and change our choice from +0 to +1 on exactly -d[i] days.
What happens if I change the choice for day j <= i from +0 to +1? I get a +1 to all d[k] s.t. j <= k <= i. So, it's easy to see that if I need to overturn a choice, I should do so for the latest day on which I made a +0 choice. That means that every time I make a +0 choice, I can just push the index in a stack, and anytime when d[i] < 0, I can pop from the stack exactly -d[i] times and add (i – stack.top() + 1) to the answer.
Link — 36588535
can u please explain how is d[i] = d[i-1] + m[i-1] – m[i] + (0 or 1) this equation formed ? thankyou.
d[i-1] + m[i-1] + 1 imply the number of marks on day i-1. So the number of marks on day i equals d[i-1] + m[i-1] + 1 + (0 or 1), (0 or 1) mean the mark on day $$$i$$$ is coincided or not. => $$$d[i] = number\ of\ marks\ day\ i - m[i] - 1 = d[i-1] + m[i-1] + (0\ or\ 1) - m[i]$$$.
Can anyone explain how to solve knapsack in O(S sqrt(S))?
Test cases for 924 A were weak.
The grid size was 50 x 50. I solved the problem converting every row (considering # as 1 and . as 0) to a binary equivalent integer. Now, for every two rows with integer values, I was checking if (a == b) || (a & b == 0).
But I took it as an integer, and so it was only taking the last 32 positions in the row. I was also checking for the column, and it was valid only for the last 32 positions in the col.
With a long long integer, having 64 bits (50 required in problem), the solution should be correct.
Any testcases where the grid is of size 50 x 50. And you place random elements in the top left subgrid of size 18 x 18, it should fail.
But my code still passed the system testing.
Link to solution: http://codeforces.com/contest/957/submission/36584331
Please, help! (Task D) Why does these quadratic solutions get wrong answer on test 4. http://codeforces.com/contest/924/submission/36670452. http://codeforces.com/contest/924/submission/36671090. Firstly I calculte all pairs of points of left and rihgt side. Then i iterate over all points on left and right side and check pairs o them. I tried to find a bug in this code, but I couldn't.
P.S.: I undersand that i incorrectly calc pairs of points on the one side
My solution for div2E is giving slightly wrong ans for large testcases. Can somebody suggest why or give a smaller testcase where my code fails?
Could you describe your solution for Bonus2 of Minimal Subset Difference? Judging by the limits, it seems unlikely to be exponential, so I'm really curious to see what it is
I'm sorry that we are going to prepare another problem related to the Bouns2 approach, so please let us suspend for a while longer before revealing it. Also, we encourage people to come up with the same idea (or better optimized) individually.
Hi, please check Petr's blog out, as he mentioned a problem like Bonus2 of MSD.
Regarding Problem C: Riverside Curio 1)The number of watermarks strictly above the water level on each day=m[i] and one mark is used to mark the water level so the minimum number of marks should be >=(m[i]+1), secondly, the number of watermarks on a day[i]>=day[i-1]so we should move from left to right and take the maximum of all indices to the left of index i and m[i]+1 to assign the the number of watermarks on the day i. 2)There is a possibility that after assigning the number of watermarks on each day there might exits day[i] and day[i-1] such that day[i]-day[i-1]>1 so we should remove such adjacent false relations as day[i]-day[i-1]<=1 so initialize day[i-1]+=(day[i]-day[i-1]+1) in such cases where day[i]-day[i-1]>1 and in order to do this step traverse from right to left. My submission: https://codeforces.com/contest/924/submission/94533526