Adiv2. Consider an array A of integers in range from 1 to nk. Let's remove from A all numbers ai and all other numbers store into an array B. The array B will have (n - 1)k elements. Now for i-th kid you should output numbers ai, B[(n - 1) * (i - 1) + 1], B[(n - 1) * (i - 1) + 2], ... B[(n - 1) * (i - 1) + n - 1] (B is 1-based).
Author is Gerald .
Bvid2. Solution 1. You should write some bruteforce solution over all numbers with no more than 9 digits (number 109 should be considered separately). Bruteforce algo seems like this:
dfs( int num ) // run it as dfs(0)
if (num > 0 && num <= n) ans++
if (num >= 10^8) return
for a = 0..9 do
if num*10+a>0 then
if number num*10+a has no more than 2 different digits then
dfs( num*10+a )
ans will store the answer. After that you wrote bruteforce, you can run it and see that it works fast (that is same time for any testcase).
Solution 2. Let's build all undoubdetly lucku numbers using bitmasks. You can iterate over length of number L, pair of digits x and y, and bitmask m of length L. If the i-th bit of m is 1, the i-th digit of number should be x; otherwise it should be y. So about 103 × 210 numbers will be generated (it is very rough estimate, count of numbers will be more than 10 times less).
In this solution you should accurately process the case of leading zeroes and the case when all digits of number are same.
Author is Gerald
Adiv1, Cdiv2 Let's see how function f changes for all suffixes of sequence a. Values of f will increase when you will increase length of suffix. For every increase all 1-bits will stay 1-bits, but some 0-bits will be changed by 1-bits. So, you can see that no more than k increasing will be, where k number of bits (in this problem k = 20). Among all suffixes will be no more that k + 1 values of function f.
Now you can run over sequence a trom left to right and support an array m (or a set) of values of f for all subsegments that end in the current position. Size of m always no more than k + 1. When you go from position i - 1 into position i, you should replace m = {m1, m2, ..., mt} by m' = {ai, m1|ai, m2|ai, ... mt|ai}. After that you should remove from m repeated values (if you use set, set will do this dirty work itself). Then you should mark all numbers from m in some global array (or put them into some global set). At the end you should calculate answer from the global array (or set).
Bdiv1, Ddiv2 You should check for every edge: this one can be body of hydra or not. Let's fix some edge (u, v) (order of vertices is important, i.e. you should also check edge (v, u)). Now you should chose some set of h vertices connected with u and some set of t vertices connected with v. These sets should not contain vertices u and v. Also, these two sets should have no common vertices.
If 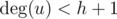 and
and 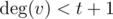 , there is no any hydra here.
, there is no any hydra here.
Orherwise, if 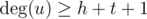 or
or 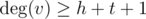 , there is some hydra in any case. Even if all vertices connected with u and with v are common, number of them so big, that you always can split them into groups of size ≥ h and size ≥ t.
, there is some hydra in any case. Even if all vertices connected with u and with v are common, number of them so big, that you always can split them into groups of size ≥ h and size ≥ t.
The last case is 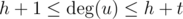 and
and 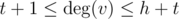 . Here you can find all common vertices in O(h + t), using array of flags. When you find the common subset, you can easy check existence of hydra.
. Here you can find all common vertices in O(h + t), using array of flags. When you find the common subset, you can easy check existence of hydra.
UPD How to find common vertices in O(h + t) using array of flgs? You should initailize that array in the beginning of program. For every check you should do following actions. Firstly in 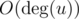 you should mark in the array all neighbours of u. After that you should iterate over all adjacent to v vertices and check value of flag in the array for every of them (in
you should mark in the array all neighbours of u. After that you should iterate over all adjacent to v vertices and check value of flag in the array for every of them (in 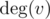 ). Vertices that have "thue" in the array will be common. Finally you should clear the array in
). Vertices that have "thue" in the array will be common. Finally you should clear the array in 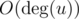 : you should iterate over all adjacent to u vertices again and mark these vertices in the array as "false". Because
: you should iterate over all adjacent to u vertices again and mark these vertices in the array as "false". Because 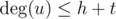 and
and 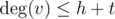 , the total complexity will be O(h + t).
, the total complexity will be O(h + t).
All edges can be checked in time O(m(h + t)). So you either find reqired edge or find that there is no required edge. Also in time O(m) you can build hydra with fixed body-edge.
This problem also has solution in 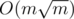 independent from values of h and t, but this solution is more complex.
independent from values of h and t, but this solution is more complex.
Author is Ripatti
Cdiv1, Ediv2 Firstly tou should emulate all process in "idle mode". Let farmer was in points (x0 + 1 / 2, y0 + 1 / 2), (x1 + 1 / 2, y1 + 1 / 2), ... , (xn + 1 / 2, yn + 1 / 2). Coordinates x0, x0 + 1, x1, x1 + 1, ... xn, xn + 1 on axis x are interesting for us. Coordinates y0, y0 + 1, y1, y1 + 1, ... yn, yn + 1 on axis y are interesting too. You should store all of them into two arrays. Also you should add to these coordinates bounds of the field.
Then you should build "compressed" field: every cell of this field means rectangle of the starting field that placed between neighbour interesting coordinates. Size of the compressed field is O(n) × O(n). Let's initally all cells painted into the white color. Now you should emulate all process again and paint all visited cells in the compressed field by the black color. During every move you will paint O(n) cells, so all process will be done in O(n2).
Now you should emulate bugs' actions. You should run DFS (ot BFS) from some border cell of the compressed field and paint all reached cells be red color.
At the end you should iterate over all compressed field and find sum of areas of rectengles corresponding to black and white cells. So, you will receive the answer.
This solution works in O(n2).
Author is Ripatti
Ddiv1 You need for every column find the lowermost cube that you can see. You will see all cubes above this cube.
Consider the city from above. You will see drid of size n × n. Now you should draw the line through every node of the grid parallel to vector v. We need know only that happens in every strip between two neighbour lines. Every column cover segment of O(n) adjacent strips.
Now you should create an array a; every element of a corresponding to one strip. This array will store maximal height of considered columns.
Then you should sort all columns in order if increasing distance from observer. In that order you should do following queries of 2 types:
Minimum on segment. This query is needed when you want find the lowermost visible cube.
Replace ai → max(ai, h) on segment. You need this query for "drawing" column in the array.
That is all solution. You just need choose some data structure that can fast do queries. You can select from: block decomposition (length of every block should be  ; because length of every query about O(n), total complexity of solution will be O(n5 / 2)), segment tree (
; because length of every query about O(n), total complexity of solution will be O(n5 / 2)), segment tree ( ), stupid array (it's O(n3), cache optimized implementaton fits in the time limit).
), stupid array (it's O(n3), cache optimized implementaton fits in the time limit).
Author is Ripatti
Ediv1 We will build the matrix constructively. At any step we will have array of groups of columns. Order of groups is defined but order of columns inside every group is unknown.
During building we will change order of rows because it is doesn't affect the answer (we can build answer using order of columns only).
Consider the way of building of the matrix. Firstly you should find the row that has maximal number of ones. You should swap this row with the first row. Aftar that two groups of columns should be created. Into the first group you should put columns that have "1" in the firts row; all other columns should be stored into the second group. The second group is "special" — see about it below.
Now you should more times search the row that has "1" in at least two groups. For every of that rows you can determine positions of all ones no more than only way. If you determined no ways, you should output NO and finish execution. After that you determined positions of ones, you should split some groups of columns into two subgroups.
About "special" group. You should take into account case when you should drop some columns from this group and insert them before all groups. You will never face with situation when it is not clear which columns should be dropped and which should not, because in the beginning you chose the row with maximal number of ones.
After repeating process than described above sevaral times, "good" rows may end. I.e. for every row all ones will be placed in no more than one group. Now you should recursively do solution described above inside every of groups of columns.
The solution works in O(n3). It can be upgraded to  , but it was not required.
, but it was not required.
UPD Also here some O(n2) solution exists based on PQ-trees, as said mugurelionut. More information here.
Author is Ripatti











I'm really new to CF, and i'd like to know if the editorials are both in English and Russian, or if it's up to the person who prepares the Round.
Thank you.
PS: If there is a gentle person who can explain briefly this solutions in English, that would be just Awesome!
Could you please explain the O(m*sqrt(m)) solution for Bdiv1 ? (at least briefly — maybe just the main ideas?) It sounds interesting to me...
I can't explain it, but you can sort solutions by Execution Time and find the fastest. Maybe it will help you http://codeforces.com/contest/243/status/B?order=BY_CONSUMED_TIME_ASC
Thanks. I will have a look, but I doubt it that anyone implemented an O(m*sqrt(m)) solution as mentioned in the editorial (i.e. independent of h and t). Moreover, even if anyone did, it doesn't necessarily mean that it would be among the fastest ones (maybe the fastest solutions take advantage of the small limits for h and t).
I was hoping that maybe Ripatti could give us some hints regarding the O(m*sqrt(m)) solution (which could work nicely, for instance, even for large values of h and t).
Here's my solution which has a complexity of O(m*sqrt(m))
We define deg(i) as the degree of vertex i
We choose a value S.
step 1:
we will analysis the complexity of step 1. Note that there wont be more than O(M/S) vertices that satisfies deg[i]>=S
we can check whether pair(i,k) is valid in O(deg(k)) time when vertex i and its neighbours are marked. so the inner loop have a total complexity of O(M). and the marking step is obviously O(N).
so this step have a complexity of M^2/S
we notice that, any solution which satisfies deg(u)>=S or deg(v)>=S will be found in the previous step. So if there exists a solution that hasnt been found yet, deg(u)<S and deg(v)<S holds.
step 2:
obviously the marking step is O(S) and the checking step is also O(S) because deg(u) and deg(v) are both smaller than S
so this step has a complexity of O(M*S).
its obvious that after 2 steps, all (head,tail) pairs have be checked.
the total complexity is O(M*S+M^2/S)
we choose S=sqrt(M) and archives a complexity of O(M*sqrt(M))
implemention: RunID 2602573
Thank you. It was a great explanation. And the nice part is that it's not difficult to implement this solution.
For problem B div1/D div2, can anyone explain how "you can find all common vertices in O(h + t), using array of flags"?
for my first code i used a dumb set intersection which is O((h+t)*lg(h+t)) which is too slow (i know set intersection can be done in O(h+t) ). how do you use array of flags?
you can just use an boolean array, index as the key
i suppose you mean vertex number? but there can be 100000 vertices so initializing the array will take O(100000) for every edge which is too much.
if you dont mean vertex number how do you use index to compare equality? the index of the vertex in an adjacency list tells you nothing about the vertex itself.
err, right, my solution timeout on test case 47. ok, i'm gonna ask the same question here...(facepalm)
Use the boolean array of size 10^5 vertices, but note that for every vertex you are testing as the head of the hydra, you only need to mark its neighbors in that array. Just before you go test another vertex, reset all the neighbors to false. This way you aren't initializing all the vertices every time you look for a hydra.
yeah, i did this, still time out, i sneakingly revere the order the edge, and passed the test.
Bdiv2: Solution 1
@Ripatti: I believe you've made a typo in the pseudocode provided for dfs().
The line: if num*10+a>_9_ then should really be: if num*10+a>_0_ then
see 2587112 for my full solution based on this approach if you'd like.
thank you, fixed
"Adiv1, Cdiv2 Let's see how function f changes for all suffixes of sequence a. Values of f will increase when you will increase length of suffix."
Why is this so? If you have the sequence as (2, 3), the xor will decrease if you increase the length of the suffix?
"For every increase all 1-bits will stay 1-bits, but some 0-bits will be changed by 1-bits."
Again how about the case 3 and 5. The xor increases, but not all 1-bits stay 1-bits. Am I missing something here?
The operation is OR not XOR
Thanks. I spent a lot of time thinking about this problem thinking that the function is XOR. My bad.
I am surprised that PQ trees are not mentioned at all in the editorial as a possible solution for Ediv1. The problem is well known as the "consecutive ones" problem and PQ trees are the standard method (as far as I know) of solving it. In fact, by using PQ trees, the time complexity becomes optimal (i.e. O(n^2)).
Here's the original paper describing PQ trees and their application to the "consecutive ones" problem: http://www.sciencedirect.com/science/article/pii/S0022000076800451# (the PDF was freely accessible when I tried it, but I cannot guarantee that it will stay like that for long)
Unfortunately (for me), I have never implemented PQ trees and trying to understand them (or reinvent them) during the contest was not feasible (not that I didn't try it :) ).
Seems that I invented well known problem)
Can someone explain the bitmask solution(different from the editorial one) of div1A / div2C?
can anyone please tell me the bitmask solution of div2 B?
You can see that n < 1e9 will contain 9 digits and it will be made of only two digits so code will look like this
few important points when n == 1e9 then add 1 in the ans since 1000000000(1e9) is not included
make sure that starting char to be stored in ans is not zero
code 87452720
thank you so much!!:)