Hello CodeForces Community!
The May Long Challenge 2018 is at your doorstep to treat you with a programming fixture for 10 exciting days. You surely wouldn't want to miss this one! Joining me on the problem setting panel are:
- Problem Tester: .o. (Suchan Park)
- Problem Authors: (Bhushan Khanale), chemthan (Trung Nguyen ), isaf27 (Ivan Safonov), nileshjha19 (Nilesh Jha), xtalclr (Jineon Baek), Slow_But_Determined (Abdullah Aslam ), altruist (Denis Anischenko), (Abishek Saini)
- Problem Editorialist: triveni (Triveni Mahatha)
- Statement Verifier: Xellos (Jakub Safin)
- Russian Translator: CherryTree (Sergey Kulik)
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese Translator: VNOI Team
I hope you will enjoy solving them. Please give your feedback on the problem set in the comments below, after the contest.
Contest Details:
Time: 4th May 2018 (1500 hrs) to 14th May 2018 (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: https://www.codechef.com/MAY18
Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
Prizes: Top 10 global and top 20 Indian winners get 300 Laddus each, with which the winners can claim cool CodeChef goodies. Know more here: https://www.codechef.com/laddu. (For those who have not yet got their previous winning, please send an email to [email protected]). First to solve each problem individually: 100 laddus (For problems common to both Divisions, only one user will get laddus for that problem).
A request to problem setters out there: Recently we are short of problem proposals in general, but more in the hard level problems. If you want to set interesting problems, please feel free to send your proposals. More details at https://www.codechef.com/problemsetting/setting.










I made order from CodeChef on November 31 previous year and didn't get it yet
Can you please send them another mail? I will ask them to check it up asap. These things shouldn't be happening at all!!
Can you tell me on which mail we should send our details?
My prize is also in queue since 26th January (I have already sent mail on [email protected] , but nobody answered).
Please try [email protected] . Also, it will be really great if you could PM me your support ticket numbers. I will ask them to hunt for those mails and deal with them urgently. :)
Wow! A Codechef round tested by legendary competitive programmer .o.. Surely this round will be terrific!
Me in every Codechef long challenge
How to solve Change the Signs problem ??
It's enough for segments of lengths 2 and 3 to be valid, longer segments can be split up to these ones. And now it's just dp[N][2][2] of position, sign of previous number and sign of the number before it with state being the smallest sum you can achieve.
I reduced the problem to you are given 1-d array and find the maximum sum subsequence with no consecutive elements.
“It’s enough for segments of lengths 2 and 3 to be valid, longer segments can be split up to these ones. ”
I didn’t use dp. I just keep the segments whose lengths of 2 or 3 is positive. I wondered why my method was wrong.
Can you please share your code?
Sure
Here's an alternate approach, using 1-D dp and segment trees, probably a bit too overcomplicated:
First observation: any element can only be multiplied by - 1 is it is strictly smaller than both its neighbours (segments of length 2 must be valid, to quote the other answer). From now on, by 'valid position', I will mean a position which can be multiplied by - 1.
Let suf[i] denote the suffix sums of the array. Then, the sum of some range [l, r] of the array can be calculated as suf[l] - suf[r + 1], and sum of the whole array is just suf[0].
Let dp[i] denote the best possible answer till position i, with the condition that position i is multiplied by -1, and nothing after i is (and of course, array is valid). dp[i] = suf[0] if i is not a valid position.
Second observation: When calculating the answer for a particular i, only the (valid) positions before it matter, since everything after it has a constant contribution to its answer being always positive.
This gives us a simple recurrence for dp: dp[i] = min(suf[0] - 2a[i], min(dp[j] - 2a[i])) = min(suf[0], min(dp[j])) - 2a[i] where 1 ≤ j ≤ i - 1 and the sum S = - a[j] + a[j + 1] + ... + a[i - 1] - a[i] is positive. (do you see why we don't need to bother about any other segments?)
Third observation: S = S + suf[i] - suf[i] + a[j] - a[j] = (suf[j] - 2a[j]) - (suf[i] + a[i])
Notice now that we essentially want the following: minimize the value of dp[j] across all positions j such that suf[j] - 2a[j] > suf[i] + a[i]; where the right side is just a constant once i is fixed, and the left side depends purely on j. This can be done fairly simply using a segment tree, and at the end, we can just find the minimum value of dp[i] across all valid i, and this is our answer. Reconstruction of the answer is also simple by simply storing extra data at each node.
(If the segment tree part is not obvious, think about this problem: given N points (xi, yi) in the plane, and some number k, find the minimum value of yi across all pairs (xi, yi) such that xi > k.)
My implementation.
You don't need any segment trees. I used 3 dp arrays, each to store optimal answer for till the ith index where the i-1 and ith indexes are "++", "-+", and "+-" respectively. Another 3 dp arrays to store the length of the shortest subsequence ending at any index i again for 3 cases of "++", "-+", "+-". Then it is a simple DP recurrence.
Oddly though, my solution always failed for some random edge case where N = 2 (the very first test on Codechef) so I just submitted a brute force for N = 2 along with my DP solution
Solution : https://www.codechef.com/viewplaintext/18545352
Yeah, that seems to be the standard solution several people have used, certainly much simpler than mine (except for your n=2??). Hence why I called mine 'overcomplicated' :)
Yeah I don't know I'm probably missing some edge case for the N = 2? IDK lol.
Is there any better solution for EDGEST than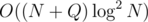 ? I did get AC, but not after spending nearly a day doing constant optimization (also the reason for the meme I made earlier).
? I did get AC, but not after spending nearly a day doing constant optimization (also the reason for the meme I made earlier).
How to solve even the first subtask of SERSUM? I know that the solution involve Lagrange interpolation, but can't come up with anything beyond that.
Is the problem RUBBER just about checking if a point is in a non-simple polygon?
Problem Rubber requires to check whether a polygon in the plane minus some points (the nails) is homotopic to zero or not. An algorithm to do so can be found in Theorem 3.22
Any good material to learn about topology? This seems like Greek to me now.
I'll try my best with Rubber as an example. You are allowed to deform the rubber the blue polygon in the picture: but you are not allowed to "jump over" the black dots that represent the nails. You want to "free" the rubber from the nails. We assume that all the nails have different x coordinate (if not you can perturb them slightly and the solution to the problem won't change). Take vertical lines along each black dot as in the picture and label them. Observe that we label the two half lines separated by each black dot differently (with capital and lowercase letters). Now we produce a word by following the polygon as it crosses the different vertical halflines. It doesn't matter at which point of the polygon we do start. In this case we obtain the word AAbcdeffedcbbcdefgGFEDCb. Now we compute the reduced word as follows: every time we find two consecutive equal letters we suppress them. For instance one first reduction will be to eliminate the first two AA and we get bcdeffedcbbcdefgGFEDCb. This correspond to deforming the path. Observe the top left corner of the polygon where it crosses the half line A twice. We can rectract the polygon a bit and eliminate the double AA. We keep reducing the word. If at the end we are left with an empty string the rubber could be liberated, if not it is not possible.
but you are not allowed to "jump over" the black dots that represent the nails. You want to "free" the rubber from the nails. We assume that all the nails have different x coordinate (if not you can perturb them slightly and the solution to the problem won't change). Take vertical lines along each black dot as in the picture and label them. Observe that we label the two half lines separated by each black dot differently (with capital and lowercase letters). Now we produce a word by following the polygon as it crosses the different vertical halflines. It doesn't matter at which point of the polygon we do start. In this case we obtain the word AAbcdeffedcbbcdefgGFEDCb. Now we compute the reduced word as follows: every time we find two consecutive equal letters we suppress them. For instance one first reduction will be to eliminate the first two AA and we get bcdeffedcbbcdefgGFEDCb. This correspond to deforming the path. Observe the top left corner of the polygon where it crosses the half line A twice. We can rectract the polygon a bit and eliminate the double AA. We keep reducing the word. If at the end we are left with an empty string the rubber could be liberated, if not it is not possible.
For the general theory of homotopy in the plane take any introductory textbook in topology. I am not very familiar with it and cannot really reccommend any.
The explanation was very helpful. Thanks a lot.
"Topology" by James Munkres is a pretty good place to start, if purely mathematically. Homotopy is introduced in chapter 9, but I think it can be mostly understood after going through chapters 1, 2 and some part of 3. I don't believe the book assumes any prerequisites either — chapter 1 takes care of that.
Rubber: The problem started to make sense after I saw this test case: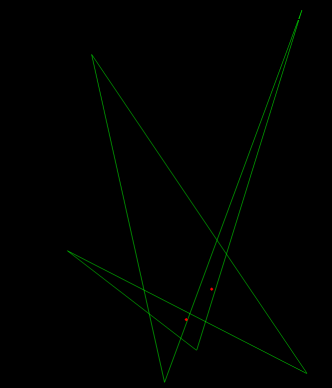
(The point is we can't look at just a single nail at a time to make conclusions. (Also 2 nails are not enough either if we extend this test case, we need many.). The solution is folding together 3 points into 2 points whenever doing that doesn't intersect with any nails. We also add extra points to avoid cases where it get's stuck, like this one.)
Sersum: No need for interpolation, but a lot of googling and FFT. (Too hard to explain in detail, just giving hints):
Use Faulhaber's formula
We can speed this up for multiple k, if we use FFT (B_k together with k! and x^(p-k+1) together with (p-k+1)!)
We can calculate the Bernoulli numbers in O(k^2) which takes about 1s out of given 6s.
If we have multiple x, we can just add them together in the Faulhaber's formula before FFT
(Now we need to solve a different problem: given an array, calculate the sum of k-th powers of it's elements for every k in [0,K])
Use Newton sums
If we construct polynomial (x-a_0)*(x-a_1)*...*(x-a_{n-1}), then it's roots are our array, so it fits nicely into Newton sums. (We can calculate the coefficients of this without interpolation, just divide and conquer multiplying left half and right half with FFT).
We can calculate Newton sums faster, if we do something like "sqrt"-decomposition with FFT. So calculate first 10000 S_i in the naive way, then FFT them together with the coefficients. Same with next 10000. That is all we need to fit into 6 seconds.
My solution does not use googling or bernoulli numbers or newton sums. Just some manipulation with binomial theorem and fft. ( For both sub-tasks, array sum powers and sum of kth powers of natural numbers)
We can use fft with fractions to achieve the former, and fft with exponential sums to achieve the latter.
Cute Observation : (a[0]0·x0 + a[0]1·x1 + .. + a[0]n·xn + .....) = 1 / (1 - a[0]x) in ring of formal power series. Can we use this to calculate sum of kth powers for given array ? Yes !.
My Submission
You are the same as tester's solution. Unfortunately, after calculating k power sums, I did the rest in stupid way, so it run quite slow which make TLM so high and some O(k^2) (constant seems small) passed :(.
Can anyone here give simplest approach to STMINCUT ?
First, let assume a[i][j] = a[j][i] (if not, we will spend some cost to make those two equal).
For all graph, it is possible to build a tree such that the minimum cut between any two vertices in that tree is the same with the minimum cut between those vertices in the original graph (such tree is called Gomory-Hu tree). So, the task is reduced to: Build a tree such that sum of a[i][j] - minE(i, j) for all pair of (i, j) is minimum (minE(i, j) mean the minimum weight of the edges on the path from i to j).
This can be done greedily by iterating over all pair (i, j) in decreasing order of a[i][j] and add edge (i, j) into the tree if i and j are not connected yet (similar to Kruskal's algorithm).
My implementation
Thank you! xuanquang1999 :)
Could someone explain their approach for EDGEST?
Okay, since nobody tells their solutions, I might share some ideas, at least. I solved only the easy subtask but still.
Firstly, the task asks you the following thing. You take an edge e1 from the first tree, insert it into the second tree, take all the other edges on the cycle produced by adding e1 and calculate the number of them which produce such a cycle in the first tree that e1 lies on it. I won't mention cases with coinciding edges, they are trivial.
The latter check can be done in O(1). With either some cases with tins and touts or segments on eulerian traversal. Here is the approach in O(n2) using the second idea.
Now you should remember that you can choose some segment on eulerian traversal that it contains all the edges on the path between v and u odd number of times and other edges — even number of times (0 or 2, of course).
So if we learn to extract only the first ones then we can make queries on segments for the first cycle check. The first thing that came to my head was Mo's algorithm. It's easy to maintain the number of times edge appears on some segment. We just need such a structure that can count the number of segments (a, b) such that given some (x, y), exactly one of x or y appears in that segment. When we add or remove edge (move border) we make an update operation on 2D-BIT :D Okay, what does it store. It stores segments in form of points on a grid, get operation just calculates the number of points of some prefix-rectangle. That was the last solution I wrote. It is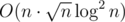 and TLs even the first subtask :D
and TLs even the first subtask :D
I believe I have an idea how to get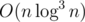 solution of it. Still, I don't really think I can implement it in such a way that it fits into TL.
solution of it. Still, I don't really think I can implement it in such a way that it fits into TL.
I think O(n log3n) won't pass cause I had 2 solutions of such complexity and both failed due to TLE in 3 cases.
My solution only involved BIT-2D, and the complexity is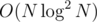 .
.
Some notation:
The idea is that, let f(u, v) be the number of edge (x, y) (from now on, we assume that in1[x] ≤ in1[y]) on the path from 1 to u of the second tree such that one of the following condition is satisfied:
in1[x] < in1[v] and in1[v] ≤ in1[y] ≤ out1[v]
in1[v] ≤ in1[x] ≤ out1[v] and out1[v] < in1[y]
Then the answer for an edge (par1[v], v) in the first tree is f(par1[v], v) + f(v, v) - 2 * f(a, v), with a being the LCA of par1[v] and v in the second tree.
Let's find an easier way to calculate those f value. Let cnt(u, a, b) the number of edge (x, y) on the path from 1 to u of the second tree such that in1[x] ≤ a and in1[y] ≤ b. Then, f(u, v) = cnt(u, r, n) - cnt(u, r, r) - cnt(u, l - 1, n) + 2 * cnt(l - 1, r) - cnt(l - 1, l - 1) with l = in1[v] and r = out1[v].
So, calculate f can be done offline by doing eulerian traverse throught the second tree and 2D-BIT. When you enter/exit an edge (x, y), increase/decrease the value of cell (in1[x], in1[y]) in the 2D-BIT by 1. Then, for all query f that end on vertex u, do appropriate query call in the 2D-BIT.
However, the constant of the this solution is very high (Each edge require three f value, each f value require 5 query on 2D-BIT). To optimize, we need to realize that 4 out of 5 query on 2D-BIT can actually be done using 1D-BIT, so the constant is reduced greatly. My solution need another (stupid) optimization (find f(u, v) naively if depth of u in the second tree is low) to get AC, and I think that there exist a test that make my solution run in more than 2s.
I think the time limit for this problem is way too strict.
Oh, so that's how it could be done! Nice approach. It seems I was moving the right direction, just missed the idea of offline queries.
Here the author claims a solution of complexity O(n log n).
Any hint for FAKEBS???
Straight up implementation. And such an ad-hoc one.
You should probably notice that there is only one path binary search can take to reach some position. The rest is just greedy ideas compressed into a couple of ifs.
Define
goal numberas the number that you want to reach to. Start binary search in a normal fashion i.e from indexes 0 to n-1. Also keep 4 integers cl,cr,okl,okr.Case 1:- The goal number is to the left of the current index. The number at the current index also leads to the left. Increment okl.
For eg:- The number at current index is 7 and goal number is 1 present to the left of 1. The number 7 will lead you to left and goal is also to the left.
Case 2:- The goal number is to the right of the current index. The number at the current index also leads to the right. Increment okr.
Case 3:- The goal number is to the left of the current index. The number at the current index leads to the right. Now we need to swap a number with this current index that will lead to the right. The nature of the number should be such that it is less than the goal number. Increment cl.
Case 4:- The goal number is to the right of the current index. The number at the current index leads to the left. Now we need to swap a number with this current index that will lead to the left. The nature of the number should be such that it is more than the goal number. Increment cr.
Now okl and okr are the numbers that are fixed and do the work for us. We don't need to swap them. However cl and cr are the smaller and greater numbers that we need. Try to see if we have enough of them (by excluding okl and okr from total_smaller_numbers and total_greater_numbers than goal number respectively). Also we can swap the numbers such that 1 cl and 1 cr number is adjusted in one swap only.
For implementation:- Code
Woah, man. This idea can be implemented in 20 lines, not 150.
yo
When will editorials be published?
Why so much delay for editorials ?