250A - Paper Work. For every folder you should take reports as much as possible. In other words, you should stop forming a folder either before the third bad report or in the end of sequence. You can easily prove that this strategy is optimal. This solution works in O(n).
Author is MikeMirzayanov
. 250B - Restoring IPv6. Firstly you should split string into substrings using ":" as separator. All empty substrings will go in the row; you should leave only one of them. Then you should calculate number of nonempty substrings and determine number of zero-blocks whicр will replace empty substring. After replacing you should increase every substring to length 4 inserting leading zeros. After all you should output the answer.
Author is Ripatti.
250C - Movie Critics. Consider some maximal by inclusion segment of movies of some genre x (this number from 1 to k). Now let's see how changes number of stresses after removing this segment. If the segment adjoins to the end of all sequence a, improvement will be +1. Segment cannot adjoin to both ends of sequence because k > 1. For some seqment [i, j] inside of sequence consider values ai - 1 and aj + 1. If they are equal, after deleting segment improvement will be +2; otherwise it will be +1.
Now you should iterate over all maximal be inclusion segments and find improvement for every of them. After that you should group all segments by genre and calculate sum of improvements inside every group. Answer will be number of genre of group that has maximal total improvement (if there are many of them, you should chose minimal number of genre).
You can implement this solution in in O(n).
Authors are MikeMirzayanov Gerald Ripatti.
250D - Building Bridge. For every point of the east river bank you should find optimal point of the west bank. After that you should chose optimal pair over all considered east points.
Well, let's fix j-th east point (1 ≤ j ≤ m). Now consider how changes total distance depending on chosing the west point. The best point is intersection of lines OBj и x = a: 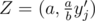 , but this point can be not present among all west points. You can see that if you will move from point Z up or down, total distance will increase. So only nearest to Z points may be considered.
, but this point can be not present among all west points. You can see that if you will move from point Z up or down, total distance will increase. So only nearest to Z points may be considered.
You can find that points using binary search. Also you can observe that after every increasing of j point Z will move in same direction; so you can support nearest points to Z usins some pointer. The third way is using such fact that during moving point over the west bank total distance initially will decrease and then increase; so you can use ternary search here.
Considered solutions work in O(m + n) and 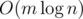 .
.
Author is Ripatti.
250E - Mad Joe. You should emulate the process. You can catch case of infinity walk if you will observe hits with concrete wall from the left and the right side. If for some floor both types of hits happened, you should output "Never".
Stupid emulation is very slow. It has complexity O(nm2) and answer can be about 1010. You should speed up stupid emulation using following way.
For every floor you should store segment of visited cells (two integers — L and R bounds). We know that under every cell of this segment all cells are non-empty. Therefore after every changing of move direction you can go through all the segment in O(1). After every one or two "teleportations" through segment you either expand bounds of the segnent or change some brick-cell into empty-cell or fall down. But actions of every type you can do no more than nm times, so this optimization improves complexety to O(nm).
Author is Ripatti.











typo under problem 250C — Movie Critics...'gerne' -> 'genre'
Oops... I always thought this word should be written as 'gerne'. My bad English...
Fixed. Thank you.
I like it :-D