Distributed Code Jam 2018 round 1 starts on Sunday, June 10th at 14:00 UTC and lasts 3 hours. This round is open for everyone who advanced to round 3 of the regular Code Jam. Top 20 contestants will earn a trip to the final round in Toronto.
This year, Google will use the old contest system for Distributed Code Jam rounds. Only C++ and Java are supported, and the versions of compilers used are ancient: GCC 4.7.2 for C++ and Java 7. Beware that GCC 4.7.2 was released in 2012 and doesn't support many new C++ features. If you are using Java, your main class must be named Main, not Solution.
As some people found out, you must have registered for Distributed Code Jam, but it wasn't required if you already had your data in the old system. In any case, you may visit this page to check that your data is there.











Where can I find compiler options they use?
There's something here (Technical information), but the local testing tool compiles for you and presumably with the same options they use.
thanks
Anyone with the contest link?
Perhaps this. Got it from the reminder letter.
Thanks
move_library_here.sh
g++ -II also need to remove
problem.hfrom myDownloadsdirectory before I download another one with the same name, otherwise it's saved asproblem (1).hLol. From the dashboard:
But now that only DCJ uses the old platform, A is always Testrun...
I think Kickstart also uses this platform
Is the number of people advancing to Final changed this year? Last year there were 20 + 1 (winner of 2016), but it seems this year has only 20 in total.
Some gotchas with the testing library on mac OS:
(Google, plz fix.)
One can also change clang to gcc-x and rebuild.
Another one on Windows: compilation errors and runtime errors are ignored by
dcj.py.Fix is in
dcj.py: make_subprocess_call_with_error_catchingreturnsubprocess.call, not zero.What a retarted system.
1) If 2 minutes passed but your solution is still being judged, "incorrect attempt" is displayed. I've spent a few minutes on some easy problem because of that, only to see AC a bit later.
2) I submitted an easy version 5 minutes before the end, and barely managed to submit a large (20 seconds before the end) because I had to wait for easy to be judged. And ofc. I saw "incorrect attempt" first and submitted the easy version again (slightly improved). The only good thing is that submitting an easy version doesn't block from submitting a hard just after that (thanks to AC from an earlier submission).
And why do I have "1 wrong try" in E? I had two correct submissions for easy. Maybe the standings aren't that final :D
The DCJ quickstart guide says:
"You will still be allowed to submit solutions to the Small dataset after one of your submissions is accepted, although the subsequent submissions will not affect your score or penalty time in any way. You can use this option to test the code you intend to submit for the Large dataset. Note that this option is still subject to the 2-minute cooldown period."
That doesn't seem to be true.
Will the practice be open after judging?
What is "too many open files for system" error message? When I want to compile my source in macOS (with default package and default commands from google), either pipe or fork/exec prompts this bug.
I thought that I used up too much resources or whatever, but I found out that my computer can't even compile this one. So I picked any random command line from this link, and everything worked fine after some point (I remember it was "ulimit -S -n 2048").
This costed me about 1hr of contest time — I was nearly giving up the contest, but very fortunately found that article somehow. What is the reason of this error message?
E:
We need to compute such recurrence: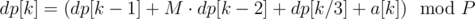
Let's compute values to dp[80] on every node. We use exactly 81 nodes. We will proceed in log(n) phases. In first phase we compute values dp[81], ..., dp[242], in second one we compute values dp[243], ..., dp[728] etc. In every phase we partition interval of interest into 81 intervals of equal length, so for example in first phase first node gets [81, 82] interval, second [83, 84] etc. Let's note that if node X wants to compute dp[k] then it computed dp[k/3] before. In each phase if node wants to compute dp[L..R] only thing he doesn't know is dp[L-1] and dp[L-2]. So we express every dp in terms of linear functions with two unknowns and after every node did that we can quickly pass info about these values in chain shape and then compute real values.
To bad I didn't debug it in time.
Yup. Also, we can use 100 nodes. The only important thing is that we should first compute at least first 100 values then. I computed first 106 or so to decrease the number of steps and thus the communication between nodes.
Points in this problem should be 30+6 instead of 12+24. The two versions are almost the same, unless there is some easy solution that I don't see.
Results are now posted. Congratulations Errichto on double win!
So first person on first pages of results of both GCJ and DCJ matches! If you look closely you can note that this is also the case for the last person on first pages xD
I spent forever trying to code a misparsed version of problem D, where the period didn't have to divide the total length... It's doable but somewhat messy:
Code, probably buggy but passes sample: https://gist.github.com/simonlindholm/e31b68fccd66a140a6d49a6f81db4c8a
My approach to D (which passes the small but times out on the large, I'd guess being a small factor too slow): - Factorise the total length to find candidate periods. - For each candidate, compute hashes of all the repetitions. Each node will get some number of complete repetitions, which it checks get the same hash, plus a prefix and a suffix for which it gets a partial hash. Each node sends the hash of the prefix, hash of the suffix and hash of the complete repetitions (if consistent) to the master to finish fixing up.
To make this efficient, use a polynomial hash function and a prefix sum of s[i]*x^i, so that the hash over any range can be computed in O(1) time. My solution unfortunately took O(log N) time per hash (to compute a power of the polynomial), and I think that's why it's too slow.
Each node will do work proportional to O(N log N + F) for F factors (the log N coming from a harmonic series, so it's probably an overestimate); the worst cases will be highly composite numbers.
(Edit: fixed the Big-O estimate)
My approach was basically this, except that instead of trying all factors of N (total length), I only tried the factors of the form N/p^i for every prime factor p of N. Then the actual period is just the gcd of all valid periods of that form. This requires only log N sets of hashes, so it passes even if we require log N time per hash.
Trying only N/p^i is enough since they give complete information on the factorization of the period, and that if p1 and p2 are periods, then gcd(p1,p2) is also a period.
I kinda don't get where you got these log factors from, but my first approach was similar, with every node partitioning its letters into suffix, internal repetitions and prefix, but then I noted that code will be much simpler if instead of checking whether s[0..L) = s[L..2L) = ... = S[(n/L -1)L..n] I will check if s[0..(n-L)) == s[L..n) :).
I wish I'd thought of that... it would have been a lot simpler to code and faster as well.
I also thought about this approach, but I didn't know how to check s[0..(n-L)) == s[L..n) in an elegant manner, so instead I checked s[0..n) = s[0..L) * (1 + x^L + x^(2L) + ... + x^(n-L)), the right part being s[0..L) * (x^n -1) / (x^L -1).
Thus I needed to calculate only hashes of all prefixes of s.
My solution: Factorize total length. Now for each possible frequency and each pair of nodes we know which substring (possible empty) from first node should be equal to substring in second node for this frequency not to fail. Just send hash of corresponding substring from 2 to node 1. Now each node know which frequencies are compatible with it. Send this info to some central node to compute answer
I have the same solution (each pair of nodes compares parts of their segments that should be equal), and it proved pretty tricky to code. There are a lot of different cases. There is even a case in which intersection of two segments consists of two non-adjacent strings, and in this case care must be taken about their order. Now I see that there are simpler solutions which send hashes to the master node.
wait, what? For given frequency intersection is always segment
My solution is quite easy I think, in edit (library code ommited)
Ah, I see. You solution only compares substrings whose positions differ exactly by
current, and my solution compares parts whose positions differ by any integer multiple ofcurrent. Basically, for every pair of nodes, it checks which frequencies are possible if only these two nodes exist, and segments belonging to other nodes can have arbitrary content.No reason to do that
I admire the diligance, but I have one question. Maybe I am missing something, but how does this solution handle the case of a very long string of A's with some noise in the middle? In that case a lot of the hashes will be the same, allthough the string is not very periodic (a long prefix and a long suffix are, but not the entire string). And aborting the equality check early seems a bad idea since somewhere in the noise there will probability be a match for the first couple of bits.
Oh, you're right. Seems fixable but only by quite messily restricting to a suffix of the hashes when finding that it's equality-dense... In theory that should still be fine; Chernoff bounds tell us that if we're cutting off after "n * (0.5 + eps)" equalities out of n hashes our probability of not finding something in that region goes down as exp(-O(eps^2 * n)) for n large, and for n small we can add a constant in that cutoff formula to get the same effect.
My solution for C (which failed on the large, but I'm confident the idea is sound):
Divide the towels into a grid, with each node getting some rectangle. For the small, this can just be vertical divisions. My attempt at large would make either horizontal or vertical divisions depending on P, but I think the idea should work more generally.
In the stack from which your towel will come, let D be the dirtiest towel taken by the time you've left. In every other stack, note the highest towel that is dirtier than D, and call these towels "filthy" (one per stack). When D is taken, every other stack must be depleted to at least the point where the filthy towel is on top, since otherwise D wouldn't be the dirtiest at that time. On the other hand, the stack containing D has always had a top towel with dirt level <= D, and so none of the filthy towels will have been taken. So the process will occur in two phases:
Given D (by dirtiness), the number of towels taken in phase 1 can be computed, by binary searching each stack (after precomputing a running maximum per stack). An outer binary search will give us the largest dirtiness of D for which phase 1 does not remove too many towels; with a little work one can prove that this is indeed the correct value of D.
Parallelism can be achieved with pretty standard techniques, mainly parallel prefix sums and reductions. I also had to rotate master nodes to keep message counts under control, and I reduced to 20 nodes to further reduce messaging overheads in the binary search.
In my solution (which passed the large in 8340ms) I did the following:
Evenly divide the stacks among the nodes (the worst case seems to be 101 stacks in which case the first node might get about 20 million towels). Then for each node determine the order in which the towels for this node are given out (using a priority queue) and determine the prefix maximums (these are the candidates for D).
Now given a value of D, a node can determine the number of towels it gives out in phase 1 by binary searching these prefix maximums. With the outer binary search (each test involves sending a query to each other node and waiting for the answer) each node can paralelly determine if it has the 'correct' value of D and if so (which will be the case for exactly one node), how many towels are taken before it, from which the final answer can easily be computed.
The final trick in my solution for reducing the message count is to use a k-ary search (I used 250) instead of a binary search.
Is this k-ary search really necessary? I assume this is to prevent master sending current value asked by binary search to all 100 nodes in each of ~30 phases of binary search, but we can pass it in chain manner.
Or we could use a different node as the master node for each iteration of binary search.
In my solution there is no master. Every node searches for the correct value of D in its own list of maximums (and only one node finds it and that node prints the answer). So the number of messages send for every node is 2*number_of_nodes*number_of_iterations and the k-ary search is necessary.
Maybe you could pass the queries of all searches in a chain instead, but it might be to slow and seems trickier to code to me. Also maybe there is a way around having to search on each node, but I don't see it yet (searching on the entire range of towels fails since it is not monotonic, it is only monotonic for the prefix maximums, but the master does not now the prefix maximums of others, or which node holds the globally k-th prefix maximum)
You can also send it as in binary tree(each vertex sends to up to 2 vertices), like in heap. I think, that should be faster, then a chain an
When I was talking with friends about stones problem I said "After you apply prefixes maximums rest is very easy" and then I noted this sentence is a solution to towels as well :D
Mind to share "rest is very easy" part?
We split the N stones into 100 parts/intervals.
Let's say you already have prefix maxima (what required some communication between nodes). Now in every part you run DP that for every stone will say in how many jumps we can get outside the interval and how far we can go with the last jump. Then you start from the leftmost interval, you already know in O(1) how many jumps will spend in this interval and you know in what stone in the second (or later) interval you will be — this is exactly what the DP gives us. So every node gets info from its left neighbour, knows in O(1) how many jumps to add to the answer, and proceeds to the right neighbour.
Thanks! What to do in case it is not optimal to cover interval in the least number of jumps? For example for interval 2 2 2 100 it is possible to get out of it using 2 jumps, but in 3 jumps you can go much much further. Should be both values passed into the next (and later) intervals?
Remember that first you take prefix maximum, so the 100 jump can be "used" later too, even if you jumped past the 100.
Example, for input:
2 2 2 100 1 1 1 1, after prefix max. we have2 2 2 100 99 98 97 96.Hence it is enough to minimise number of jumps to reach next interval (and in case of tie maximise distance travelled into next interval).
Well, that was a missing part:) Thanks a lot!
Which is what I said in first post and said that the rest is easy :D
That seems somewhat simpler than what I was doing. I only calculated the local prefix maxima (not the global ones) and then the result of a single node in the final calculation was the triplet (minimum cost to get to the next interval, maximum position we can get with that cost, maximum position we can get with a cost of one more)
I did exactly the same during the contest ;p
Is compile error counted against the penalty? Did they mention this anywhere?
It was mentioned only for code jam.
wow, all the comments from red...