Здравствуйте! На acmp.ru есть интересная задача — самая сложная задача с полуфинала ВКОШП 2016/2017 Красноярского края. Ниже приведу краткое условие.
Есть циклический массив длины n (1 ≤ n ≤ 105) из целых неотрицательных чисел (все его элементы расположены по кругу), сумма элементов которого не превосходит 109. Требуется для каждого k от 1 до n определить, можно ли разбить отрезок [1..n] массива на k непересекающихся отрезков, сумма элементов в которых равна и каждый элемент покрыт хотя бы одним отрезком. Так как массив циклический, то за элементом с индексом n следует элемент с индексом 1, таким образом, последний отрезок может переходить через границу массива.
Раньше этот пост содержал просьбу помочь, так как не проходило мое решение. После обсуждения и изучения контр-тестов, предоставленных YANORMALNOSUPERGOOD, выяснилось, что это решение и не должно проходить, так как оно основывается на жадности, после чего было придумано следующее решение: для каждого делителя si суммы всех элементов S для каждого отрезка [l, r], содержащего начальный элемент массива, при помощи бинарного поиска и префикс-сумм предпринимается попытка построить еще ki = 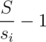 отрезков (ki ≤ n), сумма на которых в точности равна si. Если я ничего не перепутал, то это решение занимает O(count(ki)·n + sum(ki)·log(n)) ≈ O(n4 / 3·log(n)·log(log(n))) по времени. На сервере оно работает за 1.5 секунды.
отрезков (ki ≤ n), сумма на которых в точности равна si. Если я ничего не перепутал, то это решение занимает O(count(ki)·n + sum(ki)·log(n)) ≈ O(n4 / 3·log(n)·log(log(n))) по времени. На сервере оно работает за 1.5 секунды.
Вопрос: можно ли решить оптимальнее, легче (возможно, за один проход по массиву), и нет ли контр-тестов, которые должны вызывать TLE у решения выше?
UPD: Aeon и YANORMALNOSUPERGOOD показали, что оптимальнее решить можно, а именно, за время O(n·numberOfDivisors(S). Причем, в оценке участвуют только делители, которые не превосходят n. Ключевой момент — избавиться от бинарного поиска, который выполнялся sumOfDivisors(S) раз. Для этого можно перейти к динамическому программированию и для одного делителя предподсчитать определенную величину, которая позволит за O(1) отвечать на запрос о максимальном количестве искомых отрезков. Решения с указанной асимптотикой приведены в комментариях здесь и здесь.
Возможно, асимптотику можно еще улучшить, воспользовавшись тем фактом, что если мы выяснили, что для какого-то делителя суммы ответ 0, то и для всех делителей, кратных ему, ответ 0, а если для какого-то делителя ответ 1, то и для всех делителей, на которые он делится, ответ 1.











Ваше решение не находит ответ для двух столов (префикс длины 2 + суффикс длины 2).
Спасибо, понял в чем проблема, исправил. Теперь я использую тот факт, что для s — делителя S, при условии, что можно выбрать k = S / s подходящих отрезков, то должен существовать хотя бы один отрезок [l, r) (0 ≤ l ≤ r ≤ n) такой, что сумма элементов внутри него равна s. Код. К сожалению, это решение тоже не проходит, но теперь уже на 31-м тесте.
Не находит 3 (1-5, 2-3, 4). Попробуйте использовать тот факт, что если вы зафиксируете префикс длины l для самого первого блока (т.е. отрезок [0; l - 1]), то суффикс для него будет восстанавливаться однозначно (куда пойдет ноль, нас очевидно не интересует).
Спасибо! Прошло с временем 1.5 следующее решение: для каждого делителя s суммы всех элементов S для каждого отрезка [l, r], содержащего нулевой элемент, при помощи бин.поиска и префикс-сумм пробуем построить еще S div s - 1 отрезков, сумма на которых равна s.
Автокомментарий: текст был обновлен пользователем dmkz (предыдущая версия, новая версия, сравнить).
Автокомментарий: текст был обновлен пользователем dmkz (предыдущая версия, новая версия, сравнить).
Автокомментарий: текст был обновлен пользователем dmkz (предыдущая версия, новая версия, сравнить).
Насчёт вашего решения я не умеют придумывать тест против него, но интуитивно кажется, что в асимптотике где-то должно быть количество делителей суммы всех чисел. Когда я писал про префикс длины l, я имел ввиду следующий подход, работающий за O(N × divisorsCount(S)), где S — сумма значений инпута.
Пусть вы зафиксировали сумму, скажем need_sum, и хотите проверить можно ли разбить каким-то образом на группы с суммой need_sum циклический массив a. Давайте попробуем перебрать границы группы, которой будет принадлежать 0-ой элемент массива. Тут возникает сложность, ведь 0-ой элемент может содержать часть префикса массива и часть суффикса. Давайте переберем длину префикса, пусть она l, тогда сейчас отрезок элементов, с которыми в группе будет 0-ой элемент выглядит [0; l - 1], если эта сумма уже больше, чем need_sum — значит префикс такой длины и более нам уже не подходит. Теперь, зная длину префикса, однозначно можно найти длину суффикса, ведь нам нужно добрать сумму в точности до need_sum, а у нас сейчас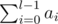 . Назовем зафиксированную на данный момент длину суффикса r. Теперь у нас остался не циклический массив, а кусок подмассива [l; n - 1 - r] и нам нужно ответить на вопрос: можно ли разбить его на группы, где сумма каждой группы будет в точности need_sum ? Предпосчитаем для каждой позиции i, позицию nexti такую, что
. Назовем зафиксированную на данный момент длину суффикса r. Теперь у нас остался не циклический массив, а кусок подмассива [l; n - 1 - r] и нам нужно ответить на вопрос: можно ли разбить его на группы, где сумма каждой группы будет в точности need_sum ? Предпосчитаем для каждой позиции i, позицию nexti такую, что 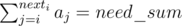 . После этого предпосчитаем для каждой позиции i, dpi = первая позиция справа, начиная с которой нельзя получить блок с суммой в точности need_sum.
. После этого предпосчитаем для каждой позиции i, dpi = первая позиция справа, начиная с которой нельзя получить блок с суммой в точности need_sum.
dpi =
Теперь мы умеем за O(1) проверять можно ли при фиксированных l и соответственно r, разбить кусок подмассива [l; n - 1 - r] на блоки суммой в точности need_sum, если это возможно, то dpl = n - r
nexti можно подсчитать двумя указателями, находить r при увеличивающемся l тоже, отсюда и вытекает, что всё будет работать за O(n × divisorsCount(S)).
UPD: OK
Даст ли что-нибудь использование того факта, что если для одного делителя ответ 1, то и для всех делителей этого делителя ответ 1, и наоборот: если для одного делителя ответ 0, то для всех кратных ему делителей ответ 0?
Решение за O(N * S1 / 3), где S — сумма чисел в массиве
Перебираем делители S, которые ≤ N, пишем для делителя k динамику dpi — максимальное количество отрезков на суффиксе префикса длины i. Переход dpi = dpj + 1, si - sj = S / k
Решение с unordered map TL
Меняем unordered map на два указателя OK
Автокомментарий: текст был обновлен пользователем dmkz (предыдущая версия, новая версия, сравнить).
Вопрос: можно ли решить оптимальнее, легче (возможно, за один проход по массиву), и нет ли контр-тестов, которые должны вызывать TLE у решения выше?Я готовил эту задачу, и помню, как двое суток пытался создать контртест к такому или похожему решению. Как видно, так и не придумал. Ответ находился быстро то по одному параметру, то по другому.