TL;DR
In this article I’m trying to explain the difference/similarities between dynamic programing and divide and conquer approaches based on two examples: binary search and minimum edit distance (Levenshtein distance).
The Problem
When I started to learn algorithms it was hard for me to understand the main idea of dynamic programming (**DP**) and how it is different from divide-and-conquer (**DC**) approach. When it gets to comparing those two paradigms usually Fibonacci function comes to the rescue as great example. But when we’re trying to solve the same problem using both DP and DC approaches to explain each of them, it feels for me like we may lose valuable detail that might help to catch the difference faster. And these detail tells us that each technic serves best for different types of problems.
I’m still in the process of understanding DP and DC difference and I can’t say that I’ve fully grasped the concepts so far. But I hope this article will shed some extra light and help you to do another step of learning such valuable algorithm paradigms as dynamic programming and divide-and-conquer. ## Dynamic Programming and Divide-and-Conquer Similarities
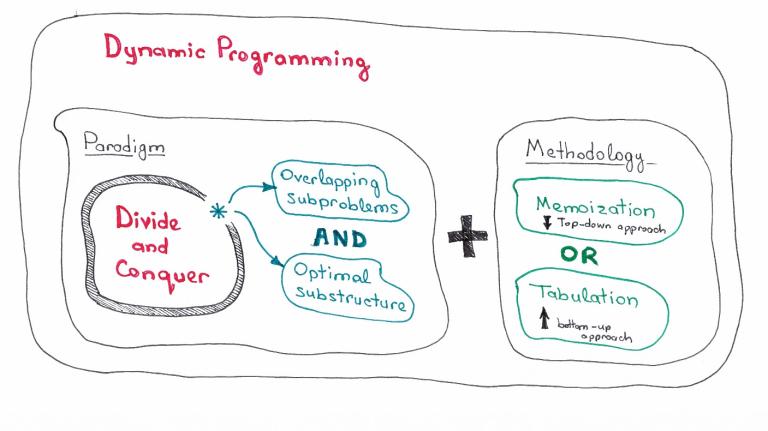
As I see it for now I can say that dynamic programming is an extension of divide and conquer paradigm.
I would not treat them as something completely different. Because they both work by recursively breaking down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem.
So why do we still have different paradigm names then and why I called dynamic programming an extension. It is because dynamic programming approach may be applied to the problem only if the problem has certain restrictions or prerequisites. And after that dynamic programming extends divide and conquer approach with memoization or tabulation technic.
Let’s go step by step…
Dynamic Programming Prerequisites/Restrictions
As we’ve just discovered there are two key attributes that divide and conquer problem must have in order for dynamic programming to be applicable:
Optimal substructure — optimal solution can be constructed from optimal solutions of its subproblems
Overlapping sub-problems — problem can be broken down into subproblems which are reused several times or a recursive algorithm for the problem solves the same subproblem over and over rather than always generating new subproblems
Once these two conditions are met we can say that this divide and conquer problem may be solved using dynamic programming approach.
Dynamic Programming Extension for Divide and Conquer
Dynamic programming approach extends divide and conquer approach with two technics (**memoization** and tabulation) that both have a purpose of storing and re-using sub-problems solutions that may drastically improve performance. For example naive recursive implementation of Fibonacci function has time complexity of O(2^n) where DP solution doing the same with only O(n) time.
Memoization (top-down cache filling) refers to the technique of caching and reusing previously computed results. The memoized fib function would thus look like this:
memFib(n) {
if (mem[n] is undefined)
if (n < 2) result = n
else result = memFib(n-2) + memFib(n-1)
mem[n] = result
return mem[n]
}
Tabulation (bottom-up cache filling) is similar but focuses on filling the entries of the cache. Computing the values in the cache is easiest done iteratively. The tabulation version of fib would look like this:
tabFib(n) {
mem[0] = 0
mem[1] = 1
for i = 2...n
mem[i] = mem[i-2] + mem[i-1]
return mem[n]
}
You may read more about memoization and tabulation comparison here.
The main idea you should grasp here is that because our divide and conquer problem has overlapping sub-problems the caching of sub-problem solutions becomes possible and thus memoization/tabulation step up onto the scene.
So What the Difference Between DP and DC After All
Since we’re now familiar with DP prerequisites and its methodologies we’re ready to put all that was mentioned above into one picture.