I was recently solving some problems on Linearity of Expectation. I was trying to solve the Coupon collector problem. The problem is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? This is how I tried to solve the problem:
E[Number of coupons needed to draw so that each coupon comes atleast once]
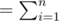 E[Number of coupons drawn till i'th coupon is drawn for the first time]
E[Number of coupons drawn till i'th coupon is drawn for the first time]
This comes from the Linearity of Expectation (Link) since independency or dependency of events does not matter.
Now, let E[Number of coupons drawn till i'th coupon is drawn for the first time] = x
This can be solved by applying the following recursive equation,
x = 1 + ((n - 1) / n) * x
On solving, we get x = n.
Thus, E[Number of coupons needed to draw so that each coupon comes atleast once] = n2
I know that I am wrong somewhere since the answer is n * Hn, but I don't know where exactly does it go wrong. I have discussed this with my friend kr_abhinav, but we couldn't find the mistake in the proof as well.










First equation is incorrect. Let X be a random variable corresponding to the total number of coupons drawn before they all are encountered at least once. Also let Yi be the total number of coupons drawn till the first draw of i-th coupon. You claim that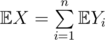 , I guess the reason is that you think that
, I guess the reason is that you think that 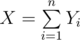 holds always. But every coupon draw counts only once in X, but can count as many as n times in the sum on the right (for example, first draw always counts in each of the Yi).
holds always. But every coupon draw counts only once in X, but can count as many as n times in the sum on the right (for example, first draw always counts in each of the Yi).
Thanks for the explanation :D ! We got so engrossed in thinking why linearity is not working that we never considered the fact that the decomposition itself might be incorrect!