wallcrawler's blog

271D-Good Substring!! Can't this problem be solved with single hash as in Rabin-Karp Rolling hash!! HELP NEEDED!!
By wallcrawler, history, 6 years ago, In English

I was solving this problem with the use of single hash and got wrong answer which means conflicts are arising. I've seen other users submission, they've solved it using double hashes, so I was wondering that can't this problem be solved using single hashing. Link to my submission:

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Single Hash : http://codeforces.com/contest/271/submission/37988095

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks mate....could you tell me one thing that in the power array you are storing powers of p = 123, why it is not overflowing since n can be upto 1500. And another thing I think I did exactly same thing as your's could you review my code for a minute pal!! Please.... Your kind help would be appreciated.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Overflow is same as modulo 2e64

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh....thanks found a new thing :)

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry for disturbing you again... but won't it cause a signed integer overflow...!!

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          You are counting only the no. of hashes,it only matters for the hashes to be equal

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I get it what you're saying, but do we have to take the prime number to be fairly big, i mean can't we take p to be 31 instead of 123, i'm getting wa at 31 but ac on 123...

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              there must be anti-hash TC,so you are having WA.Double hashing provides less probability for collisions.I just tried 123 and it worked!!

              → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Possibility of collision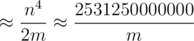 , you can not use int32 modulo, it is not safe for u. If it will be helpful, my solution uses single prime modulo 261 - 1.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you so much!! please could you elaborate further how did you reached the conclusion for collision probability!! Thanks :)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I writed tutorial about rolling hash for beginners, see Minimizing the probability of collision. In this problem we need to compare each pairs of strings in set of n(n + 1) / 2 strings, so it is n4. Maybe in this problem we need to count only compares strings with equal length, maybe someone will help to accurately assess this.

      → Reply