Hi there! Imagine you're participating in codechef long challenge and you see a problem from chemthan asking you to calculate some sums of powers like 1p + 2p + ... + np for all p from 0 to k. You immediately understand what's going on here and take Faulhaber's formula from your wide pants, do ya? Just take a look at it!
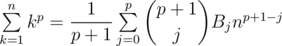
Beautiful, right? Wrong! This formula is dumb and it's hard to understand and remember! Why would you ever think about Bernoulli's number on any contest which lasts less than a week? And what the hell are those Bernoulli numbers?! Here is what you should do:
Let Sp = 1p + ... + np. Consider its exponential generating function (EGF):
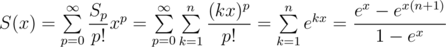
Now you can simply find S0, ..., Sk by finding inverse series for 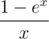 and multiplying it with
and multiplying it with 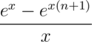 . Enjoy your power sums without Stirling and/or Bernoulli numbers!
. Enjoy your power sums without Stirling and/or Bernoulli numbers!
Exercise: Solve this problem in 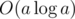 .
.
P.S. Yes, you basically perform the same calculations as in Faulhaber's formula, but now you hopefully understand what you're doing.











First of all, you don't need to remember Faulhaber's formula, you only need to know that it exists and interpolate.
Also, these solutions are substantially different, because Faulhaber's formula finds Sp(n) for fixed p and all n, and yours finds it for fixed n and all p.
I don't really agree with you here because calculating inverse to you calculate nothing but EGF for Bernoulli numbers so approaches are exactly the same, but with different interpretation.
you calculate nothing but EGF for Bernoulli numbers so approaches are exactly the same, but with different interpretation.
And I think, you should be more precise about what do you mean by all n. If it's all n from 1 to N then you don't seem to need any special formulas at all, you can calculate it in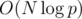 . If you mean fixed p and arbitrary single n then my solution allows you to do so as well.
. If you mean fixed p and arbitrary single n then my solution allows you to do so as well.
And yes, you're right, interpolation also allows to solve this particular case with both n and p fixed in O(p). But as you may see at the beginning of my post, I wanted to write specifically about case when n is fixed and you need to calculate values for all p from 0 to k.
I understand that it might be a bit misguiding since I only paste formula here without further comments, but it was supposed to be considered as convolution:
So in this interpretation you clearly may calculate values for all p.
Sorry, I forgot that evaluating polynomial takes O(p) time which is not even better than interpolation.
I got that your solution works for all p for 0 to k. But still, for fixed n and p, I don't see a way to make it work in linear time, like interpolation. Calculating single coefficient of product is easy, but here we have quotient. So it seems, your solution is only good when we need to calculate the sum for different p. In other cases additional logarithm with pretty big constant from inverse seems bad.
That is true, for fixed n and p Lagrange interpolation is better. Though it worth mentioning that you seemingly can't apply interpolation in this problem while similar EGF can be calculated in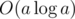 to solve the problem.
to solve the problem.
How to find inverse series? I know there is a post by vfleaking on codeforces on the same.I read it several times but still I can't understand . Please tell me ,how can we find inverse series?
link
I have paragraph about it here.
i am thinking of Maclaurin expansion for finding inverse series for (1-e^x)/x but it's hard to implement is there any other way to do this
using some complex analysis
this problem too but here lagrange interpolation is much better https://codeforces.com/contest/622/problem/F
It should follow from these expressions that for p ≥ 0
The first three cases are:
p = 0: S0 = n
p = 1: S0 + 2S1 = n2 + 2n, and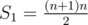
p = 2: S0 + 3S1 + 3S2 = n3 + 3n2 + 3n, and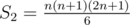
Therefore, the following recursive expression can be derived for p ≥ 1
where the base case is S0 = n
Yep, there is this formula but you can't calculate fast enough with it.
I wonder why this recursive formula may not be fast enough for modular arithmetic with large n and small p, as both (n + 1)p + 1 and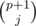 may be computed recursively in reasonable time when p is small. Furthermore, the division by (p + 1) operation may be preformed using modular multiplicative inverse. Any plausible explanation for such presumed inefficiency would be appreciated.
may be computed recursively in reasonable time when p is small. Furthermore, the division by (p + 1) operation may be preformed using modular multiplicative inverse. Any plausible explanation for such presumed inefficiency would be appreciated.
Because you'll have to compute each of Sj for j from 0 to p.
But isn't it required in the problem statement to compute Sp for all p from 0 to k? It seems that the only difference between both requirements is the change in the parameter names.
I'd just like to clarify a doubt — Is it possible to solve these types of sums using Lagrange interpolation ?
Yes, but only if you have to calculate it for single fixed n and p.
Thanks for clarifying :)
Finally nice and short text about it! You are definitely my favorite blog writer since now :D Big +
Great to see such feedback! Now you really have to learn Russian so you can enjoy even more of my blogs X)
"Now you can simply find S0, ..., Sk by finding inverse series for (1-e^x)/x and multiplying it with (e^x — e^(x(n+1)))/x"
how did you come up with the above statement?
I understand the logic before that, i.e. EGF for Sp = S(x) = (e^x — e^(x(n+1)))/(1-e^x)
now if my understanding is correct then the coefficient of x^p in EGF of S(x) would be the answer to (1^p + 2^p + 3^p ....... n^p)/p!.
but I didn't understand how you got to the statement I mentioned before. Do you mean that (e^x — e^(x(n+1)))/(1-e^x) ===> (x/(1-e^x)) * ((e^x — e^(x(n+1)))/x)
where (x/(1-e^x)) ==> inverse of (1-e^x)/x
I also know that (x/(e^x-1)) is generating fn for Bernoulli numbers
even if this is the case, I don't get how should I proceed.
Would be great if you could explain a bit more
Thanks
Do you mean that (e^x — e^(x(n+1)))/(1-e^x) ===> (x/(1-e^x)) * ((e^x — e^(x(n+1)))/x)
Yes.
How to proceed further?
Read editorial of this problem it covers relevant background required. This is nice problem imo. It has detailed editorial as well.
I have both these problems opened in other tabs :-p
The codechef problem also refers to the 1st CF problem in its editorial
still not able to get it
I will give it another try though
btw when the author says "multiplying it with (e^x — e^(x(n+1)))/x"
he means to consider "(e^x — e^(x(n+1)))/x" as another EGF and then using convolution.
Meaning, EGF1 * EGF2
where EGF1 = x/(1-e^x) and EGF2=(e^x — e^(x(n+1)))/x
And then we need to use convolution C(x)=A(x)B(x) generates the sequence Cn=SUM(n,k)AkB(n-k)
Am I right?
Yeah. Its convolution of EGF1 and EGF2. FFT/NTT.
I read the tutorials again and tried to solve it on paper
I managed to understand the algorithm to take inverse of $$$F(z)$$$ with $$$R_{2n}(z) = 2R_{n}(z) - F(z)R_{n}(z)^2 (mod z^{2n})$$$.
Please let me know if this seems right:
$$$S(x) = (e^x - e^{nx+x})/(1-e^x)$$$
$$$ = (x/(1-e^x)) * (e^x - e^{nx+x})/x$$$
Now expanding these 2 terms we get:
1st term := $$$1/ (\sum_{k = 0}^m x^{k}$$$/(k+1)!)
2nd term := $$$ \sum_{k = 0}^m x^{k}$$$/(k+1)! — $$$ \sum_{k = 0}^m (n+1)^{k+1}x^{k}$$$/(k+1)!
For first term we can take inverse series and then multiply it by second term using FFT
After getting the final polynomial, the coefficient of $$$x^p$$$ will be $$$\sum_{k=0}^n k^p$$$
Please let me know if my understanding is correct
Thanks
Well, its no more an imagination, check out NOV20 Long Challenge qn CHEFSSM. Nice short Blog btw, proved quite useful !!