Hello, codeforces!
The community wants so the community gets it! :D Here it is, my very first blog about tasks and algorithms. At the beginning I've decided to post my entries on codeforces, maybe I'll switch to something different if it becomes uncomfortable.
To pour the first blood I decided to choose a task from one of the old ONTAK camps. Task's name is "different words" (you can submit here). The statement goes as follows:
You are given n words (2 ≤ n ≤ 50 000), every of length exactly 5 characters. Each character can be a lowercase letter, an uppercase letter, a digit, a comma... basically, it can be any character with ASCII code between 48 and 122 (let's say that k is the number of possible characters). A task is to find all pairs of indexes of words which are 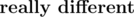 . Two words are
. Two words are 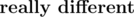 if they differ at all 5 corresponding positions. So for example words
if they differ at all 5 corresponding positions. So for example words 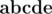 and
and 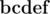 are really different and words
are really different and words 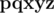 and
and 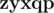 are not, because in both of them the third character is
are not, because in both of them the third character is 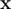 . As there can be many such pairs (up to
. As there can be many such pairs (up to 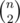 ), if there are more than 100 000 pairs, then the program should print that there are only 100 000 and print this number of pairs (arbitrary chosen).
), if there are more than 100 000 pairs, then the program should print that there are only 100 000 and print this number of pairs (arbitrary chosen).
Please, note that this task comes from the contest which took place a few years ago, so don't think about bitsets. :P
So, how can we attack this problem? At first, you may think about some meet in the middle. It turns out to be hard, even if you can come up with something with k3 in complexity, then it'll probably be multiplied by n. O(k5) is also too much. Inclusion-exclusion principle unfortunately also won't be helpful, as we want to find those pairs, not only count them, and working on sets of words won't be so effective.
The biggest problem is that k is big. If it'd be, let's say, up to 10, then it'd be solvable in some way, but I won't go deeply into this solution, cause it isn't interesting and k is of course bigger. But I've mentioned small k. Why couldn't we dream about even smaller k? If k would be up to 2 (so words would consist only of digits 0 and 1) then this task would be trivial. We'd just group words which are the same, and for each word its set of really different words would be the group with words where every zero is changed into one and vice versa. But again, k isn't small...
Buuuuut, we can imagine that it is! Let's say that we assume that characters with even ASCII characters are "new zeros" and characters with odd ASCII characters are "new ones". Then for sure if two words are really different with these assumptions, then they are really different without them, cause if they'd have this same character at some position, then this character would change into this same "new character". This allows us to find some pairs, unfortunately not all of them, but the way definitely looks encouragingly.
If we've found some of the pairs, maybe we should just try one more time? But how should we change characters now? Now comes an experience: if you have no idea what to do or you don't want to do some complicated construction, then just do something random! So we could randomly change every character into zero or one and then run our algorithm for k equal to 2 — match groups of opposite words. What's the probability for a fixed pair that we'd find it during one run of our algorithm? If we already know what we've assigned to each character of the first word, then on every corresponding position in the second word there should be a different character — for each position we have a  chance, that this assigned character will be correct, so we have probability equal to
chance, that this assigned character will be correct, so we have probability equal to 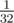 that the whole word will match.
that the whole word will match.
What's the number of needed runs? Looking at limits we can guess that it could be a few hundred. Let's calculate the probability of fail if we'd repeat algorithm 600 times. The probability that we wouldn't find some pair is equal to 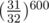 , the probability that we'd find it,
, the probability that we'd find it, 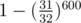 of course, and finally, the probability that we'd find all of them (or some 100 000 of them) is equal to
of course, and finally, the probability that we'd find all of them (or some 100 000 of them) is equal to 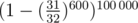 which is greater than 0.999, so it's definitely enough.
which is greater than 0.999, so it's definitely enough.
There is one more thing. Consider words 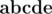 and
and 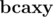 . They are really different. Let's say that we've assigned 0 to a. Then we have to assign 1 to b. Then we have to assign 0 to c. Then we have to assign 1 to a. So there is a problem... At first glance, it might look problematic, but it turns out that it's easy to fix it. We shouldn't just assign zeros and ones to characters. We should assign them to pairs (character, position). Then everything will go well.
. They are really different. Let's say that we've assigned 0 to a. Then we have to assign 1 to b. Then we have to assign 0 to c. Then we have to assign 1 to a. So there is a problem... At first glance, it might look problematic, but it turns out that it's easy to fix it. We shouldn't just assign zeros and ones to characters. We should assign them to pairs (character, position). Then everything will go well.
Total complexity is something like O(n·600·log(n)), but we can get rid of the log factor by using hashmaps.
Sooooo, it's the end of my first blog, sorry if it's too long. I hope that you've found this task useful and interesting. What do you think about this format, what was missing, what was bad? It'd be great to see a feedback from you. See you next time! :D











It's cool but this idea is not mind blowing I think, maybe something harder.
Nice hashing method
Better than most blog posts on CF I would say
Problem difficulty and post length are pretty good for my taste
。・゚゚・(>д<)・゚゚・。 Where's my shoutout? :/
This
is my favourite trick for tackling difficult problems:
It's like bitset, only more random.
You should be a little bit risky for the 3rd item. Unfortunately in this case probability theory isn't working on you mostly)
This reminds me of https://xkcd.com/628/:
Can anybody translate this article, because lots of the CF users are speak speak Russiоan))?
Сделаю кртакий перевод, передающий идею Есть очень много строк(до 50000), каждая состоит из 5 символов ASCII c номерами от 48 до 122 Нужно посчитать количество строк, которые совершенно разные, то есть у них нет ни одного одинакового символа на одинаковой позиции Например abcde и bcaed Если пар больше 100 тысяч, то вывести 100000.
Давайте каждому четному по ASCII символу присвоим 1, а нечетному 0 и удем теперь сравнивать двоичные строки, это делать гораздо легче. Очевидно что если такие двоичные строки разные, то они разные и до преобразований, но если одинаковые, то до преобразований могли быть и разные. Как можно посчитать тут количество пар при таком разбиении? Мой метод — буду рад кто предложит оптимальнее: Сортировка с компаратором, делим на группы одинаковых. тогда легко посчитать, что если например получилось три группы с количеством одинаковых строк в каждой x, y и z, то ответ будет x*y + x*z + y * z
Теперь, рандомно присвоим нашим символам новые 1 и 0, то есть каждый символ также всегда будет 1 или 0, но уже не привязан к четности ASCII. И снова делаем то что выше Автор вычислил, что с огромной верояностью 600 таких рандомов двдут нам полный ответ. Итоговая асимптотика O(nlog(n)*600)
Еще автор предлагает фичу для сортировки, шифровать символ не просто 1 или 0, а парой (1 или 0, позиция символа), что позволит избежать строк как abcde bcaxy, но вот это я не совсем понял и буду рад если кто-то напишет подробнее.
Seems like up/down voting is also performed randomly for the comments under this post. Why are you guys down-voting his comment?
I don't know, maybe it's because of my low rate))
Thanks for blog! It was very educational to me.
Can someone explain me solution with bitset for this task?
I didn't really code it. But, I think it works in this way.
For each (position, character) pair, create a n bits bitset and initially set all bit to 1. Let denote it as B(p, c). There are (5 × 75) such many bitsets.
For each string si, if p-th character of si is c, set i-th bit of B(p, c) as 0.
Then, for i-th string, the possible candidates to pair up is the 1 bits of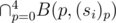 . One can use
. One can use
_Find_nextfunction to extract each candidate bit one by one.Thanks !
I understood idea :)
(edited)
Lol. Main idea of having mapping from chars to {0, 1} is not working what invalidates many statements you claimed and then you fix it at the end. Your thinking process during contest can look like this, having intermediate ideas, hacking them and fixing them, but don't confuse the reader by stating something clearly false ("for each position we have a 1/2 chance, that this assigned character will be correct, so we have probability equal to 1/32 that the whole word will match.") and continuing saying more false things keeping this confusion as if nothing happened. Already at this point you should note that these events are not independent and suggest way of fixing this and only after that provide an analysis of probability of success in overall. Thanks for writing this, it's a nice problem and nice idea, but please work on keeping general flow of text more reasonable.
EDIT: Lol, this was -40, but now it is +17, interesting.
Yea, I have to agree with you, it was possible to do it better :/ Sorry for confusing.
I would recommend checking out Solving Math Problems Terribly on Quora if you haven't seen it before. The idea is that the guy goes through his thought process of solving a math problem rather than giving a slick proof that seems like magic leaps of intuition were suddenly made. It seems like you are trying to do a similar thing here, where you shed light on your own problem solving process rather than just spitting out the correct algorithm.
Here are some example posts, if you're curious:
Post 1
Post 2 (This is solving a difficult Putnam problem, and he said he's planning to solve some IMC questions this way as well)
Post 3
Alon Amit <3. I love reading his posts. Actually I am also a fan of presenting thinking process, not just polished end product. As opposed to Alon's way, I think I do not describe paths which led me to nowhere, but when I am aware that resulting proof/algorithm may look like taken out of nowhere I usually describe how I came up with such idea. Even red coders are just mere people, even though we may sometimes came up with something brilliant, hoping that we will ace average competition on Codeforces thanks to having brilliant idea in every problem is futile. Vast majority of problems can be actually solved by following reasonable paths consisting of small steps and experience and knowledge can lead us in good direction.
Regarding this post, following path "1) Think of easier version of problem and solve it, 2) Think whether we can reduce our original problem to that easier version" by introducing problem for k=2 is a very good example of presenting how we can come up with something magical by following standard routine consisting of small steps. But the issue I talked about before can be fixed without negatively influencing appearance of "raw thinking process"
Make a different mapping for every position.
Well, that's exactly how I solved that problem back then. :P
An awesome task, though!
Let me try to take a jab at a deterministic solution: say that for each subsequence we store the positions where it occurs. E.g. if we have the sequences abcde, acekk, akcke then a_c_e maps to {1, 3}. This datastructure will have size ~n25.
Then for a given five digit string we can count the number of 'really different' words in some range [l, r] using inclusion/exclusion — consider all 25 - 1 subsequences and use the datastructure + binary search to find how often they occur in [l, r]. This takes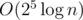 time.
time.
So now we iterate over all elements one by one. At position i, we want to find all 'really different' pairs of words (j, i) with j < i. So we can use binary search over [0, i) to find all indices where the number of such pairs changes between [j, i - 1] and [j + 1, i - 1] (then (j, i) is a pair). This will take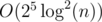 per occurrence, which I hope is fast enough (but might not be :-) ).
per occurrence, which I hope is fast enough (but might not be :-) ).
Wow, the idea with ranges is great! Blog's doing its job :D
I think if you use dynamic segment trees as your data structure, you can combine the two binary searches into one to cut a factor, like in COT.
factor, like in COT.
You can avoid the increase in space complexity by only storing nodes with two children (and the roots of course).
Time complexity: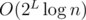 per occurrence. Space complexity: O(2Ln) where L = 5 is the length of the strings.
per occurrence. Space complexity: O(2Ln) where L = 5 is the length of the strings.
If anyone want to implement this, here is the problem link.
thanx hoxor
Unfortunately, this page doesn't work anymore :/ I mean that it won't judge your solution...
Shit :( I thought "MAIN will no longer be supported" was supposed to mean it will no longer receive updates. However, one can still get the judge data from the "Useful Resources" tab and test offline. :D
szkopul.edu.pl is the new replacement of MAIN, where you can submit your solutions.
https://szkopul.edu.pl/problemset/problem/wTy-sxQCIKry0Ml-6RvM0L78/site/ is a link to this problem. However, note that submission judging seems to be turned off for the duration of CEOI.
https://sio2.mimuw.edu.pl/c/wiekuisty_ontak2013/p/
The problem in Polish is called "Różne słowa".
Nice blog:) I have a little doubt.
Why do we have to assign 1 to a again here, because a was already assigned 0? Aren't we assigning 0 or 1 randomly to each character once? Sorry if I understood it wrong.
If I understand correctly, the author means "Then we have to assign 1 to a if we want it to not match with c", which causes a problem because 0 is already assigned to a. This messes up the calculation of probabilities from earlier, as pointed out here by Swistakk. To overcome this, the assignment is done independently for each position.
It's consoling to know that people read my posts hidden because of too many downvotes, haha :D.
Also
Not sure why you got downvotes in the first place, but currently your comment is at +17. Vote patterns here are too weird ¯\_(ツ)_/¯
boooo, we already have Petr's blog, you are just copying his idea, you just want contribution, you are next Swistakk, go away
How does the program keep track of how many pairs have been found?
You can store them in a hashset.
ᅠ
When should we expect the next blog? :)
It's comfortable for me, that I'll rather be summoning old tasks, so I have no strict deadlines, but I already have a few ideas queued up, so the answer is "soon" :D
That's so cool trick :D it reminds me of this task, the idea of simplifying numbers to only [0, 1] could make the problem too way easy. keep it up.
write two more blogs and you'll beat the second place in contributions by the largest fuckin' margin ever
Great post.
It would be perfect if you could add your code for these tasks too.
how could you actually store the groups and then comparing each word with its opposite ? I tried representing a word with a bitmask and then using an unordered_map<int, vector> to group every word, but I think the problem is when I tried to compare two words (which is essentially doing a nested loop of the two vectors to create the pairs), but for every iteration it will find the same pairs as before (and possible more or even less) which just lead me to tle, any suggestion ?
here's my code as reference [https://pastebin.com/eZ44HBYH], I tried doing some optimizations, that's why it looks little bit weird by now, but I hope it's understandable