https://www.geeksforgeeks.org/count-number-triplets-product-equal-given-number/
Can someone provide a faster solution.
Constraints : 1 <= n <= 1e5
1 <= x,A[i] <= 1e7 for all 1<= i <=n
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 00:21:13 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Auto comment: topic has been updated by ryuga222 (previous revision, new revision, compare).
Auto comment: topic has been updated by ryuga222 (previous revision, new revision, compare).
Hint:
Let p, q, r be elements in array A such that p*q*r==x.
p, q, r will be factors of x (including 1 & x).
1 <= x <= 1e7
Therefore, upper bound of number of factors of x is 2*square_root(1e7).
thanks. understood it.
it can be done in O(n*factors(x)*accesstime(frequency table)) but I guess there will be much more efficient solutions.
Have three frequency tables(Maps/arrays/or other DS) for counting the frequency of a particular divisor of X. Table 1 will store number of ways to get value y(divisor of x) using just 1 number from the array. Table 2 will store number of ways to get value y using 2 numbers from the array. Table 3 will store number of ways to get value y using 3 numbers from the array.
Initially all values in the table is 0.
Now process the array from left to right(1..n) for an element a in the current position and for all possible divisors(d) of X we are going to update all the tables. if a doesn't divide d then the tables remain same else let p=d/a. Then table3[d]+=table2[p] i.e to get d using 3 divisors with one of them as a then we need to know the number of ways to form p using two divisor till the elements that we have seen previously. Similarly table2[d]+=table1[p] and table1[a]+=1.
Make sure for each element first update the table 3,then table 2 then table 1 as 3 depends on 2 which again depends on 1.
Now after processing all the elements of the array the answer is table3[X].
thanks, understood it.
Solution
We can do it in (factors(x))^2 if we keep a hashmap or any similar one. You can google and find out that there are max 400 divisors for any number less than 1e7 which makes it even pass a (factors(x))^3 solution as my (factors(x))^3 solution was passing in the contest. Let me know if you have any problem in understanding any part of the code.
understood it. Do you have a link to the question where I can submit and try the solution??
Even though this isn't appropriate for a contest, there exists a randomized solution in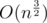 by reducing the problem to 3SUM, since
by reducing the problem to 3SUM, since 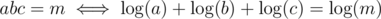 .
.