Thanks bmerry for posting his solutions, we gently took some of them as a base for editorial.
Problem author: VadymKa
Problem developers: riadwaw, malcolm
static class SquareInside {
final int inf = (int) 1e9;
public void solve(int testNumber, InputReader in, PrintWriter out) {
int n = in.readInt(), m = in.readInt();
char[][] s = new char[n][];
for (int i = 0; i < n; i++) {
s[i] = in.readWord().toCharArray();
}
int minX = inf, maxX = -inf, minY = inf, maxY = -inf;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (s[i][j] == 'B') {
minX = Math.min(minX, i);
minY = Math.min(minY, j);
maxX = Math.max(maxX, i);
maxY = Math.max(maxY, j);
}
}
}
out.print((minX + maxX) / 2 + 1);
out.print(' ');
out.println((minY + maxY) / 2 + 1);
}
}
Problem author: VadymKa
Problem developers: riadwaw, malcolm, Kostroma, Errichto
int len = 400;
cout << string(len, '5') << "\n";
cout << (string(len - 1, '4') + '5') << "\n";
Problem author: malcolm
Problem developers: yarrr, Edvard, malcolm, Errichto
static class Rectangle {
public Point topLeft, bottomRight;
public Rectangle(Point topLeft, Point bottomRight) {
this.topLeft = topLeft;
this.bottomRight = bottomRight;
}
public Rectangle intersect(Rectangle other) {
if (other == null) {
return null;
}
int x0 = Math.max(topLeft.x, other.topLeft.x);
int y0 = Math.max(topLeft.y, other.topLeft.y);
int x1 = Math.min(bottomRight.x, other.bottomRight.x);
int y1 = Math.min(bottomRight.y, other.bottomRight.y);
if (x0 > x1 || y0 > y1) {
return null;
}
return new Rectangle(new Point(x0, y0), new Point(x1, y1));
}
}
private void solve() throws IOException {
int rectanglesCount = nextInt();
Rectangle[] rectangles = new Rectangle[rectanglesCount];
for (int i = 0; i < rectanglesCount; i++) {
Point topLeft = new Point(nextInt(), nextInt());
Point bottomRight = new Point(nextInt(), nextInt());
rectangles[i] = new Rectangle(topLeft, bottomRight);
}
Rectangle[] prefixIntersection = new Rectangle[rectanglesCount + 1];
Rectangle[] suffixIntersection = new Rectangle[rectanglesCount + 1];
prefixIntersection[0] = suffixIntersection[0] = new Rectangle(
new Point(Integer.MIN_VALUE, Integer.MIN_VALUE),
new Point(Integer.MAX_VALUE, Integer.MAX_VALUE)
);
for (int i = 1; i <= rectanglesCount; i++) {
prefixIntersection[i] = rectangles[i - 1].intersect(prefixIntersection[i - 1]);
suffixIntersection[i] = rectangles[rectanglesCount - i].intersect(suffixIntersection[i - 1]);
}
for (int i = 0; i <= rectanglesCount; i++) {
if (prefixIntersection[i] != null) {
Rectangle intersection = prefixIntersection[i].intersect(suffixIntersection[rectanglesCount - i - 1]);
if (intersection != null) {
out.println(intersection.topLeft);
return;
}
}
}
throw new AssertionError();
}
Bonus: Solve the problem, if you need to find intersection of some n - k of n rectangles, if k ≤ 10. Without data structures.
Problem author: Errichto
Problem developers: zemen, Errichto, Kostroma, riadwaw
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
using ld = long double;
const int mod = 1e9 + 7;
signed main() {
#ifdef LOCAL
assert(freopen("test.in", "r", stdin));
#endif
int n;
cin >> n;
map<int, int> a{{INT_MIN, 1}, {INT_MAX, 0}};
set<int*> non0{&a.begin()->second};
for (int i = 0; i < n; ++i) {
string t;
int x;
cin >> t >> x;
if (t == "ADD") {
auto it = a.lower_bound(x);
assert(it != a.begin());
--it;
int ways = it->second;
auto m = a.emplace(x, ways).first;
non0.insert(&m->second);
} else {
auto m = a.find(x);
assert(m != a.end() && m != a.begin());
auto it = prev(m);
auto& w = it->second;
w = (w + m->second) % mod;
non0.insert(&it->second);
non0.erase(&m->second);
a.erase(m);
for (auto it2 = non0.begin(); it2 != non0.end(); ) {
if (*it2 == &it->second) {
++it2;
} else {
*(*it2) = 0;
it2 = non0.erase(it2);
}
}
}
}
int res = 0;
for (auto p : a) {
res = (res + p.second) % mod;
}
cout << res << '\n';
}
Problem author: zemen
Problem developers: yarrr, Kostroma
void solve(__attribute__((unused)) bool read) {
int n;
cin >> n;
vector<int> b(n, 0);
for (int i = 0; i < n; ++i) {
cin >> b[i];
}
int mx = *max_element(all(b));
int start_pos = -1;
for (int i = 0; i < n; ++i) {
if (b[i] == mx && b[(i - 1 + n) % n] != mx) {
start_pos = i;
break;
}
}
if (start_pos == -1) {
if (mx == 0) {
cout << "YES\n";
for (int i = 0; i < n; ++i) {
cout << 1 << " \n"[i + 1 == n];
}
return;
}
cout << "NO\n";
return;
}
auto a = b;
for (int i = 1; i < n; ++i) {
int pos = (start_pos - i + n) % n, prev_pos = (start_pos + 1 - i + n) % n;
a[pos] += a[prev_pos];
if (i == 1) {
a[pos] += mx;
}
}
cout << "YES\n";
for (int x : a) {
cout << x << " ";
}
cout << "\n";
}
Problem author: Errichto
Problem developers: Kostroma, malcolm
struct Point {
int x, y;
Point() {}
Point(int x, int y) : x(x), y(y) {}
void scan() {
cin >> x >> y;
}
auto key() const {
return make_pair(x, y);
}
bool operator < (const Point& ot) const {
return key() < ot.key();
}
bool operator == (const Point& ot) const {
return key() == ot.key();
}
Point operator + (const Point& ot) const {
return Point(x + ot.x, y + ot.y);
}
li sqr_dist() {
return x * 1LL * x + y * 1LL * y;
}
void normalize() {
auto g = gcd(x, y);
x /= g;
y /= g;
}
};
struct Hasher {
size_t operator () (const Point& pt) const {
return pt.x * 2352345 + pt.y;
}
};
enum Type {
INSERT = 1,
REMOVE = 2,
QUERY = 3
};
struct Query {
Type type;
Point pt;
int dist_id;
void scan() {
int type1;
cin >> type1;
type = Type(type1);
pt.scan();
}
};
void solve(__attribute__((unused)) bool read) {
int Q;
cin >> Q;
vector<Query> queries(Q);
map<li, vector<Point>> all_points;
vector<li> dists;
set<Point> have;
for (int i = 0; i < Q; ++i) {
queries[i].scan();
auto& pt = queries[i].pt;
if (queries[i].type != QUERY) {
all_points[pt.sqr_dist()].push_back(pt);
dists.push_back(pt.sqr_dist());
} else {
pt.normalize();
}
}
make_unique(dists);
for (auto& q : queries) {
q.dist_id = (int)(lower_bound(all(dists), q.pt.sqr_dist()) - dists.begin());
}
vector<vector<char>> has_point(dists.size());
vector<vector<Point>> points_by_dist_id(dists.size());
vector<vector<vector<Point>>> sum_points(dists.size());
unordered_map<Point, pair<int, int>, Hasher> point_position;
for (auto& item : all_points) {
make_unique(item.second);
int dist_id = (int)(lower_bound(all(dists), item.first) - dists.begin());
has_point[dist_id].assign(item.second.size(), false);
points_by_dist_id[dist_id] = item.second;
sum_points[dist_id].assign(item.second.size(), vector<Point>(item.second.size()));
for (int i = 0; i < item.second.size(); ++i) {
point_position[item.second[i]] = {dist_id, i};
for (int j = 0; j < item.second.size(); ++j) {
sum_points[dist_id][i][j] = item.second[i] + item.second[j];
sum_points[dist_id][i][j].normalize();
}
}
}
unordered_map<Point, int, Hasher> on_line;
unordered_map<Point, int, Hasher> good_pairs;
auto change_on_line = [&] (Point pt, bool add) {
pt.normalize();
if (add) {
++on_line[pt];
} else {
assert(on_line[pt] > 0);
--on_line[pt];
}
};
int n_points = 0;
for (auto& cur_q : queries) {
auto& pt = cur_q.pt;
int dist_id = cur_q.dist_id;
if (cur_q.type == INSERT) {
++n_points;
int pos = point_position[pt].second;
assert(!has_point[dist_id][pos]);
change_on_line(pt, true);
for (int i = 0; i < points_by_dist_id[dist_id].size(); ++i) {
if (i == pos || !has_point[dist_id][i]) {
continue;
}
++good_pairs[sum_points[dist_id][i][pos]];
}
has_point[dist_id][pos] = true;
} else if (cur_q.type == REMOVE) {
--n_points;
int pos = point_position[pt].second;
assert(has_point[dist_id][pos]);
change_on_line(pt, false);
for (int i = 0; i < points_by_dist_id[dist_id].size(); ++i) {
if (i == pos || !has_point[dist_id][i]) {
continue;
}
--good_pairs[sum_points[dist_id][i][pos]];
}
has_point[dist_id][pos] = false;
} else if (cur_q.type == QUERY) {
pt.normalize();
cout << n_points - 2 * good_pairs[pt] - on_line[pt] << "\n";
}
}
}
Problem author: zeliboba
Problem developers: Kostroma, riadwaw
private static final int MAX_WIDTH = 10000;
private static final int QUERIES = 5;
public static final long INF = 20000000000000000L;
long[][] memo = new long[QUERIES + 1][MAX_WIDTH + 1];
long dp(int guesses, long l) {
if (guesses == 0) {
return l;
}
if (l > MAX_WIDTH) {
return Math.min(INF, dp(guesses, MAX_WIDTH) + l - MAX_WIDTH);
}
if (memo[guesses][(int) l] != 0) {
return memo[guesses][(int) l];
}
long ans = l;
for (int i = 0; i < l; ++i) {
ans = dp(guesses - 1, ans);
++ans;
}
ans = dp(guesses - 1, ans);
return memo[guesses][(int) l] = Math.min(ans, INF);
}
private void run() throws IOException {
long l = 1;
long r = dp(QUERIES, 1);
for (int queriesNext = QUERIES - 1; queriesNext >= 0; --queriesNext) {
List<Long> query = new ArrayList<>();
long curL = l;
for (int i = 0, e = (int)Math.min(l, MAX_WIDTH); i < e; ++i) {
long end = dp(queriesNext, curL);
query.add(end);
curL = end + 1;
}
assert r == dp(queriesNext, curL);
out.print(query.size());
for (long x: query) {
out.print(" ");
out.print(x);
}
out.println();
out.flush();
System.out.flush();
int ans = readInt();
if (ans < 0) {
return;
}
if (ans > 0) {
l = query.get(ans - 1) + 1;
}
if (ans != query.size()) {
r = query.get(ans);
}
assert dp(queriesNext, l) == r;
}
}
Problem author: Kostroma
Problem developers: Kostroma, riadwaw, gchebanov, malcolm
const int C = 5032107 + 1;
int lp[C];
int fred[C];
int num_primes[C];
const int MAX_DIVISORS = 7;
const int MAX_ANS = 2 * MAX_DIVISORS;
int max_left[MAX_DIVISORS + 1][C];
int max_border[MAX_ANS + 1];
vector<int> cur_primes;
vector<int> divs;
void get_divisors(int n) {
divs = {1};
while (n > 1) {
int p = lp[n];
n /= p;
int sz = divs.size();
for (int i = 0; i < sz; ++i) {
divs.push_back(divs[i] * p);
}
}
}
void solve(bool read) {
vector<int> pr;
for (int i = 2; i < C; ++i) {
if (lp[i] == 0) {
lp[i] = i;
pr.push_back(i);
}
for (int j = 0; j < pr.size() && pr[j] <= lp[i] && i * pr[j] < C; ++j) {
lp[i * pr[j]] = pr[j];
}
}
fred[1] = 1;
for (int i = 2; i < C; ++i) {
int p = lp[i];
int cur = i / p;
if (cur % p == 0) {
fred[i] = fred[cur / p];
num_primes[i] = num_primes[cur / p];
} else {
fred[i] = p * fred[cur];
num_primes[i] = num_primes[cur] + 1;
}
}
for (int i = 0; i < C; ++i) {
for (int j = 0; j <= MAX_DIVISORS; ++j) {
max_left[j][i] = -1;
}
}
memset(max_border, -1, sizeof(max_border));
int n;
cin >> n;
int Q;
cin >> Q;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
a[i] = fred[a[i]];
}
vector<vector<pair<int, int>>> queries(n);
vector<int> res(Q);
for (int i = 0; i < Q; ++i) {
int l, r;
cin >> l >> r;
--l; --r;
queries[r].push_back({l, i});
}
for (int i = 0; i < n; ++i) {
get_divisors(a[i]);
for (int d : divs) {
int first_add = num_primes[a[i]] - num_primes[d];
for (int prev_ans = 0; prev_ans <= MAX_DIVISORS; ++prev_ans) {
int cur_left = max_left[prev_ans][d];
int cur_ans = first_add + prev_ans;
if (cur_ans <= MAX_ANS) {
relax_max(max_border[cur_ans], cur_left);
}
}
}
for (int d : divs) {
int first_add = num_primes[a[i]] - num_primes[d];
relax_max(max_left[first_add][d], i);
}
for (auto q : queries[i]) {
res[q.second] = MAX_ANS + 1;
for (int cur_ans = 0; cur_ans <= MAX_ANS; ++cur_ans) {
if (max_border[cur_ans] >= q.first) {
res[q.second] = cur_ans;
break;
}
}
assert(res[q.second] <= MAX_ANS);
}
}
int sum_ans = 0;
for (int i = 0; i < Q; ++i) {
cout << res[i] << '\n';
}
}











It is really funny that I used totally same constructive algorithm in B task, same amount of 9 and all other digits :)
How to solve C if we are asked to find any point which lies in maximum number of Rectangles?
Let's compress all values and sort points by x-coordinate. Now we can see that there is two types of events: some rectangle "opens" and some rectangle "closes". So we can solve this problem with scanline on x-axis using any data structure that can add 1 on [l, r], subtract 1 on [l, r] and tell a position of maximum value in all structure (i.e. segment tree is good for this task).
SerezhaE how will you find the corresponding y-coordinates?
We have a segment tree built on y-axis, therefore for each y we know how many rectangles cover point (xcurrent, y). I think it is not hard to determine an y in which maximum value is reached – just start at the root of segment tree and further at every step go to the son with bigger maximum value.
I think scanline technique on x coordinate while maintaining a segment tree on y coordinate would be helpful in that case. Actually, I coded that solution during the contest, which wasted me like 30 minutes or so. XD
Find the intersecting segments in X and Y axis, then merge both results to get intersecting rectangle. It can be solved easily in O(n log n) using multisets: 42187139
Why so many downvotes?
Some Intuition on solving Problem E:
Notice that b1 = a1 mod a2, so we can write a1 = b1 + x1a2 for some non-negative integer x1.
Similarly a2 = b2 + x2a3. By substituting back continuously we have a1 = b1 + x1b2 + ... + x1x2...xn - 1bn + x1x2...xna1.
Hence x1x2...xn = 0 or b1 = b2 = ... = bn = 0. Also xi can be zero (i.e. ai = bi) only if bi - 1 < bi. by the definition of modulo operation. Fix some aj = bj satisfying the above condition, then generate appropriate aj - 1 and so on such that ak > bk - 1 for every k.
Very nice, thank you.
I don't know how to generate aj - 1.
Could you tell me what do these mean?
The condition for appropriate ak - 1 is ak - 1 > bk - 2 , i.e. bk - 1 + xk - 1ak > bk - 2 or xk - 1ak ≥ bk - 2 - bk - 1 + 1. If RHS > 0 then xk - 1 ≥ ceil((bk - 2 - bk - 1 + 1) / ak).
Thank you very much!!!:)
Can anybody tell me what is wrong with my solution for problem C. I have used same concept as in editorial but am getting WA on testcase 14. Solution
UPD: NEVERMIND FOUND A TYPING MISTAKE
you'r algo is right.But the Problem is the way you print answer. See you'r last line in code.
this one cout << p << "\n" << suf[1] << endl;
My code is not expected to reach there cauz if it reached there then there is not such point possible, so I put that line for debugging purpose.
Also it is reaching the end in testcase 14.
The code given in the editorial for problem D seemed too complicated to me. So, I got the idea from the editorial and then read vntshh's solution which was very helpful to understand it. With the help of that, I wrote a commented solution for the problem. Here is the code, if you need any help: 42211321
You can replace the add(a, b) statements with (a + b) % mod, and it will still work. The functions are there just to avoid overuse of the % operation, as it is an expensive operation as compared to addition and subtraction. Further adding a lot of %s makes the code look messy.
Well, maybe modulo operation is just a little bit slower than addition and substraction, but, first of all, you do
c = a + bwhen c is ll, butaandbare ints, so you have no profit of this thing. Also, in substraction, you even didn't changed thec's type. As of mult, it's even worse. You still using the%operator (so no boost in performance) and beside that, the multiplication itself is definitely wrong and would cause an overflow on big numbers(here it probably would not, because of the constraints, but ifpwould bep <= 10^10consider multiplication a pair of these). My point is, if you wanna do it — do it right, or don't at all.please explain solution of problem B
Considering the constraints of this problem, you just have to find 2 string(numbers) that alone would have max digit sums, but when added would have the minimum(1). So, a simple way to do this is just create 2 string (any way you want), when first string would be
'9'*x + '0'*(x-1) + '1'and the second is just'9'*x.+is concatination,c*xis repeatingxtimes charc. Why? Because when added they would result in'1' + '0'*(2*x-1), so the digit sum is one. X can be 1000 for example.I didn't find any better alternatives for multiplications, so using mod. It won't overflow as multiplication is left to right associative, multiplication with 1ll converts it into a long long, and later the answer modulo 1e9+7, must be an int, so I return an int.
I use the sub operation when 0 <= a, b < mod. Note that a-b can not be <= -mod. So, even if it becomes negative, the absoute value of the result will never exceed mod-1, so adding mod converts the answer to a positive number. Furthermore, even if the answer is non-negative, it cannot exceed mod.
I accept that in c = a + b, c must have been an int. I wrote this function some time back, and not paying much attention to whether 2*(mod-1) (which is the max. value of a + b) will fit into an int or not, I took the result into a long long variable, but yes int will probably do in that case. So, Sorry for that.
aandbare ints. But, following today's "trends" you can see more problems involving modular arithmetics using the 64-bit ints, and then, your mult wont work. You can google for log n modular multiplication, if you are curious.Yeah, keep downvoting, show the codeforces' community actual face.
What is test 57 of problem E? My code is showing TLE on test 57 though its O(N). Here is the link to the code http://codeforces.com/contest/1028/submission/42212637
test: 2 1 2
when j equal n-1,
while(i != j)work infinitelycan anyone give better explanation for problem B.
You can make another two strings to solve Problem B.
44444445+55555555=100000000
you can get shortest string a and b using this algorithm:
if(n<=5) a='5',b='5',n=0; so s(a)>=s(n) and s(b)>= s(n) and s(a+b)=1 well less or equal to any n. else { a='5',b='5',n-=5; while(n>=4) a='4'+a,b='5'+b,n-=4; }
because of when n-=4, s(a)+=4 and s(b)+=5, so it can ensure that s(n)<=s(a) and s(n)<=s(b).
I am getting heap buffer overflow in problem C while it runs fine on my computer. Can somebody check my code. 42215352
instead of cs* tmp = (cs*)malloc(sizeof(cs*)); you should write cs* tmp = (cs*)malloc(sizeof(cs));
It works. Thanks
In problem D, what is the reason for adding m + 1 instead of m in the answer for the undetermined directions of remaining orders?
If the values of the undetermined n ADD orders are v1, v2, ... vn (in ascending order), so in one possible assignment all of them can be sell orders, or the first one is buy and the rest are sells, or the first two are buys and the rest are sells, ...... or all of them are buys. These are n+1 possible assignments.
Alternative solution for problem C:
Let x1, x2, and y1, y2 be the maximum two left x-coordinates and bottom y-coordinates of the rectangles, respectively. Then the answer is one of those four combinations, i.e. (x1, y1), (x1, y2), (x2, y1), (x2, y2).
What's the reasoning behind it?
First, there's such a point (x, y) that satisfies the condition (possible answer) and its x value is the x-value of some rectangle, and likewise y-value. (*)
WLOG, assume that x1 <= x2 and y1 <= y2. (These are the same values as I assumed in the above comment). Then if x < x1 or y < y1, then this point would not be in at least two rectangles, that's why it must be the case that x >= x1 and y >= y1. Combining this with (*) proves the statement.
Would it?
In this case, actually all four combinations can be the answer.
The solution to the problem http://codeforces.com/contest/1028/problem/C is almost the same as that of this problem http://codeforces.com/contest/1029/problem/C cool to have two consecutive rounds with similar problems.
"Bonus: Solve the problem, if you need to find intersection of some n - k of n rectangles, if k ≤ 10."
I suppose it is very standard task to find a place where biggest number of rectangles intersect (no matter whether it is n-1, n-10 or 2137 for n=1e5). You simply sweep them from left to right with appropriate segment tree. It was given as a task on Polish OIG long ago which is contest for <=15 year old guys :P
Come on man, it's not interesting. Better find a solution in O(nk2).
Seems, like the following works: Solve independent for X and Y. Every rectangle is just segment on axis X and the same for Y. Now we can easy find in O(N × log(N)) all X-es, which covered by at least n - k rectangles(now segments), there will be O(K) such x-es, after do the same for y and after that brute every such point in O(N). Is it ?
Maybe it's not very interesting, but it seems like you guys missed it :D. Nevermind. Could you explain your solution? (I presume it is not solution mentioned here already 2 times since this one contains from sorting)
from sorting)
Lol, of course we didn't miss it)
Our approach is the following: the x-coordinate of the result will be either one of the k + 1 minimum right x-borders or one of the k + 1 maximum left borders. The same with y. So we have a solution in O(nk2), which is very easy and fast to write :)
can you explain for Case k = 2 ...
Hint: solve problem for segments first, not for rectangles. If all segments intersect, then the leftmost right border lies inside their intersection. So if you erase any two segments, others will intersect in one of the 3 leftmost right borders anyway, if they intersect at all, because in the worst scenario you erased these two segments which had two leftmost right borders.
I actually solved problem C with this approach, for k = 2.
can we solve G without dp?can we say that dp(l,q)=((l+1)^q-l)
In problem F, can you explain why number of points (x, y) with x^2 + y^2 = C is equal to the number of divisors of C after removing all the prime divisors of 4k+3 form?
I don't know if there's a natural bijection between divisors and positive solutions to x2 + y2 = C; but I know that both numbers are equal to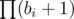 where bi are the exponents in the prime factorisation of C (assuming all prime factors are of the form 4k + 1; other primes won't increase the number of solutions) (the formula is off by one if C is a square, because then there is a solution with y = 0 that is counted by
where bi are the exponents in the prime factorisation of C (assuming all prime factors are of the form 4k + 1; other primes won't increase the number of solutions) (the formula is off by one if C is a square, because then there is a solution with y = 0 that is counted by 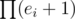 ).
).
Here's a sketch of how to derive the formula using Gaussian integers (they might seem scary, but I think the theory is also very beautiful):
First, note that N(x + iy) = x2 + y2 is a multiplicative function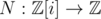 ; that is, N(z1·z2) = N(z1)·N(z2).
; that is, N(z1·z2) = N(z1)·N(z2).
Second, recall that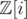 has unique factorisation; that is, any
has unique factorisation; that is, any  can be uniquely expressed as a product of "Gaussian primes" and a unit (one of 1, i, - 1, and - i). (There is the slightly annoying fact that each Gaussian prime has 4 associates including itself, but really they are the same. You can avoid this annoyance by picking your favourite among the associates and only using that one for factorisations, like how, in
can be uniquely expressed as a product of "Gaussian primes" and a unit (one of 1, i, - 1, and - i). (There is the slightly annoying fact that each Gaussian prime has 4 associates including itself, but really they are the same. You can avoid this annoyance by picking your favourite among the associates and only using that one for factorisations, like how, in  , you might write - 15 = ( - 1)·3·5 instead of - 15 = 1·( - 3)·5; we prefer 3 over - 3.) Now since the norm is multiplicative, and units have norm 1, you can determine N(z) from the multiset of Gaussian primes in the factorisation of z. Since we want positive integer solutions, z = x + iy has to lie in the first quadrant, so we will always have 1 choice of unit for any given multiset (if C is a square, our formula also counts the solution with y = 0). So the number of solutions is the number of multisets of Gaussian primes such that the product of the norms is C.
, you might write - 15 = ( - 1)·3·5 instead of - 15 = 1·( - 3)·5; we prefer 3 over - 3.) Now since the norm is multiplicative, and units have norm 1, you can determine N(z) from the multiset of Gaussian primes in the factorisation of z. Since we want positive integer solutions, z = x + iy has to lie in the first quadrant, so we will always have 1 choice of unit for any given multiset (if C is a square, our formula also counts the solution with y = 0). So the number of solutions is the number of multisets of Gaussian primes such that the product of the norms is C.
Finally, we need the classification of Gaussian primes: each Gaussian prime either has norm 2 (only one such Gaussian prime), p = 4k + 1 ( two Gaussian primes for each p), or q2 (q = 4k + 3) (only one Gaussian prime for each q). So the multisets are not too hard to count: If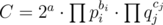 , with
, with 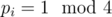 and
and 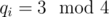 , then the number of multisets is 0 if some cj is odd, and
, then the number of multisets is 0 if some cj is odd, and 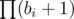 otherwise. (The only choice is in how to choose the primes of norm pi = 4k + 1: you need to distribute bi among two Gaussian primes, so there are bi + 1 possibilities.)
otherwise. (The only choice is in how to choose the primes of norm pi = 4k + 1: you need to distribute bi among two Gaussian primes, so there are bi + 1 possibilities.)
Also, I guess the limits on x, y were increased. The maximal number of solutions for C ≤ 2·1129042 seems to be 196, which is achieved by C = 52·13·17·29·37·41·53 = 12882250225. However, only 172 of the solutions have both coordinates ≤ 112904. For the record, here's a program that generates the points with unnecessary efficiency.
Wow, too much new knowledge. Thanks for your response!
For bonus task C :
Sweep only on x first, now one can prove that there will be at most 2*k + 1 points(while sweeping), where there are n-k rectangles above it. For each of these x sweep on y to find if there is a y that actually contains n-k rectangles.
Complexity O(n*k*logn);
2*k + 1 points because -> suppose I reach a x where there are n-k rectangles above on the subsequent points the number of rectangles may increase decrease or remain saim. In worst case it can form the pattern n-k, n-k+1, .. n , n-1, n-2 .. n-k.
Solution : 42217561
For Problem C, You can use multiset to get O(n log n) with a simpler solution 42241507
1700 ms, using "n log n" solution. Let's see why.
No fast input.
Let's count log n operations actually. So we have 4 log n in input, so
O(4*N log N). + 12 log n operations in computing intersections(notice thefind()operations), soO(12*N log N). In result we haveO(16*N log N). TYI,log2(10^5) ~= 17.Summing up, your constant is almost as high as
log Nmultiplier, which means, you have almostO(N log^2 N)solution.I hope you understand that 300 ms is not that far from the TLE, so next time i suggest you to optimize your solutions.
Thank you for your details analysis !
I actually find that prefix and suffix array way(editorial) harder and ugly.(Maybe it's just me)
Well i added Fast IO to the same solution and got AC with 982 ms 42251111.
It's still far slower that this random submission of 180 ms i picked, 42249815.
But mine is much cleaner, you might agree.
Yeap, as for cleanness of code, definitely. As for time, of course, asymptotic is different, nothing surprising.
I wrote a very similar solution during the contest but with fast input and it passed in about 900 ms. But anyway it can be optimized by keeping track only of the maximum 2 and minimum 2 of bottom left x & y and top right x & y respectively. It will be O(N).
For bonus C: X, Y can't be answer if we find k rectangles such that x2[i] < X, or if there exist k rectangles such that x1[i] > X. Similarly for Y. Let's sort x2, y2 in ascending order, x1, y1 in descending order. We get that x1[k] ≤ X ≤ x2[k], y1[k] ≤ Y ≤ y2[k]. Then check all possible 4·k2 variants.
Solution: 42165553.
Phew. Solved G by casework, complexity O(4·104) and even that comes from just building the query lists, all decisions are O(1). It goes like this:
If we're considering a range [m, M] with m ≥ 104, the solution is just 104 + 1-nary search, for which it's easy to calculate the maximum possible value of M - m + 1 given the number of remaining questions. Since we need to ask for at most one number until getting an answer > 0, the smallest possible value of the number in the first query is uniquely given: 204761410474.
The optimal 2-question strategy without the 104 constraint is just to ask about 2m, 2(2m + 1), 2(2(2m + 1) + 1) etc., using as many numbers as we can, so that in the next question, we'd have at worst M = 2m - 1 and could ask about all numbers in the range [m, 2m - 1].
Let's assume we got answer 0, since this is the only interesting case. The next question is for some number x < 104. Now, depending on the answer,
Now there are 2 queries left, we have M = 20468426 and m = 2047 and there isn't much of a choice. Since the last query needs to contain up to 10000 consecutive numbers, the largest number must be 20468426 - 10000, the second largest 20468426 - 1 - 2·10000 etc. This way, we can find 2045 numbers, the last of which is 16382. There are 2 numbers left and they can be decided based on the 2-query strategy with small M: 2·2047 and 2(2·2047 + 1), which are 4094 and 8190.
As it turns out, if the answer is 2 now, we have m = 8191 and M = 16381, so M = 2m - 1, so this strategy proves that the bounds really are tight — the paths in the decision tree correspond to disjoint sets of answers.
The above is an excellent example of how NOT to solve programming problems.
For problem C: Rectangles, is there a solution using convex hull technique? Can someone explain it to me.
In problem H, shouldn't it be relax best[k+dist] with dp[val][k] not dp[val][dist]?
I found a typo in the solution for Problem H,
Before doing this for i, we need to update best array: for each val | ai and aival having dist primes in factorization and for each k≤7 relax best[k+dist] with dp[val][dist]. Then all queries with right border equal to i can be answered in O(Mans) time, where Mans≤14.We should relax best[k + dist] with dp[val][k] instead of dp[val][dist].I have a solution for C with O(n) and also for bonus problem with O(k*n). My submission: my_submission Initial result is 1st rectangle. I do a for loop from 2 to n and find intersecting rectangle of the result and each rectangle from 2nd to n-th. If intersecting rectangle is empty, I will skip this rectangle and dont include it in the result, but I keep it in an archive. When size of the archive is 2, it means I skip 2 rectangles and will have wrong result. Then, if this happen, I make sure that these 2 rectangles must be a part of the final result, so I break the for loop, do a for loop again from 1 to n with initial result is intersecting rectangle of 2 rectangles in the archive. Final result is initial rectangle after for loop. For bonus problem, I also use this technique with condition to break the first loop is the size of archive exceed k instead of 1. Then with each rectangle in k+1 rectangles in the archive, I will do a for loop from 1 to n and try to find valid result and stop when I get an valid one.