In Mo's Algorithm, we sort the left pointer by using sqrt(N).
However if we consider two left pointers a and b such that a<b then (a/c)<(b/c) where c=sqrt(N). Thus it won't matter if we sort it by a<b or (a/c)<(b/c).
I know I am missing something, but I can't figure it out.










In Mo's, if we have (a / c) = = (b / c) then we sort queries on the basis of the right pointer, in which it is possible that some query [l1, r1] will come after [l2, r2] even when l1 < l2.
While sorting it just on the basis of the left pointer will not ensure us O(sqrt(N)) time complexity.
I have no idea what you are talking about. In Mo's algorithm we categorize based on left pointers (put in sqrt bucket) then sort by right pointers. Converesly, it is possible to categorize on right pointers and sort by left pointer but that's weird so I don't see an obvious reason to do so.
We never categorize by left/right pointer AND sort by the same pointer (there would be no point in doing so).
If you have an apple, then you have a fruit. But if you have a fruit, you don't necessarily have an apple.
What you are missing is that
(a/c)is actuallyfloor(a/c), soa<bdoes not imply(a/c)<(b/c). Trya = 5, b = 6, c = 4To understand Mo's algorithm, see LanceTheDragonTrainer's reply.
Sorting by (a/c)<(b/c) is splitting the array to blocks of size c and sorting by which block the left pointer is in. Let's analyze running time according to c, n, q (n/c blocks of size c):
We want to minimize according to c. Choosing
according to c. Choosing 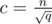 we get
we get 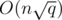 while choosing
while choosing  we get
we get 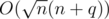 . Even though the first one is always faster (according to math, but while ignoring the small change in constant), they probably have no difference in practice, especially when n = q (but the more they differ, the better the first one is in comparison to the second one).
. Even though the first one is always faster (according to math, but while ignoring the small change in constant), they probably have no difference in practice, especially when n = q (but the more they differ, the better the first one is in comparison to the second one).
Notice that by the formula, sorting by a < b is having c = 1, which has a complexity O(n2) worstcase.