Sorry for the long blank of AGC. Meanwhile there were lots of big tournaments like GCJ, TCO, FHC. Some of our writers were also busy with helping IOI in Japan. I hope we will be able to hold AGCs more frequently from now.
AtCoder Grand Contest 027 will be held on Saturday (time). The writers are camypaper and sugim48. This contest counts for GP30 scores.
Contest duration: 140 minutes
The point values will be 200 — 700 (400) — 900 — 1100 — 1300 — 1900.
Let's discuss problems after the contest.











what a nice problem C is!
C was a very cool problem. B seemed like it would be a boring problem at first, but turned out to be pretty fun. The only thing I don't really understand is why the contest had a partial scoring option for N < 2000 on B. Was there some obvious quadratic solution? It seemed like everyone who got the 400 points for that question got the 700 shortly after, implying they just had a bug with one or two cases, but nothing regarding TLE (this was my situation as well).
How to solve B and C ? For B it was very difficult to find a greedy solution .
It's hard to find a greedy solution because greedy doesn't work for B :).
Unfortunately it's one of those questions that is made a lot easier by just writing out the math. Say you have x1 < x2 < x3. On a certain dropoff run where you pick up some subset of robots, it's obvious that you should pick them up from right to left. Then, if you write out the algebra, you'll see that the cost of picking up all three on the same run is 5x3 + 5x2 + 7x1 + 4X, and the cost of picking up any two of them and the third one separately will be 5x3 + 5x2 + 5x1 + 5X.
More generally (and this is easier to see when you are actually writing the algebra), if you are picking up different robots at coordinates x1, x2, ..., xk where x1 < x2 < ... < xk, the total cost will be 5xk + 5xk - 1 + 7xk - 2 + 9xk - 3 + 11xk - 4 + ... + (2k - 1)x2 + (2k + 1)x1 + (k + 1)X.
Well, that's useful to know. But, how do we pick our subsets that we take on each trip? And how do we figure out how many trips to take? Intuition says that you should probably (?) take everything in a continuous interval on a certain trip. But let's think about it more. Say you take 2 trips. Then, we want to assign 5, 5, 5, 5, 7, 7, 9, 9, 11, 11, ... as multipliers to the various xi. However, it's clear we should do this greedily (i.e. put smallest multipliers on the largest numbers). So, this would imply that our two trips are actually completely interleaved!
It turns out that this is pretty much the solution. Iterate on the possible number of trips from , and with prefix sums we can calculate the cost of each simulation. It'll come out to
, and with prefix sums we can calculate the cost of each simulation. It'll come out to  by the whole
by the whole 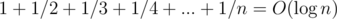 thing.
thing.
C was a bit weirder than B, but I'll try and explain my thought process clearly. Basically, we know that if there is a cycle such that every vertex in the cycle has an A-neighbor and a B-neighbor that are both in the cycle, then the answer is "Yes". The reverse direction (that this is necessary for the answer to be "Yes") is a bit harder to see, but you can do some hand-wavy justification by saying that on every path you can force one more character until it's not possible to add a particular character, or something like that.
So, finding such a cycle seems difficult, because the vertices have a recursive constraint, and it's not easy to see how to resolve that. So let's not find the cycle right away, and instead consider vertices that are "good".
We'll first call all vertices good. Then, for any good vertices that do not have a good A-neighbor and a good B-neighbor, we add them to a queue to be deleted.
When we have a vertex v in our queue, we take it out and do multiple things. First, we say that v isn't good anymore, and then we delete all the outgoing edges. If any of v's good neighbors no longer have any good A-neighbors or if they no longer have any good B-neighbors, then we add them to the queue to be deleted.
We continue this until the queue is empty, and then we see if there is a remaining cycle of good vertices. As qlmupi points out in a comment below, this process will either end in no more vertices being labeled good or a graph having a cycle, so it's not actually necessary to check whether a cycle remains, but I did anyway.
i understand this,thanks very much Kognition !
Could you please explain me the question of C? I think: "_If the graph is connected and exist 2 character 'A' and 'B' then we can always contruct string consisting of 'A' and 'B'?_ ". Am I wrong somewhere?
Sorry xxxcxxx ,i don't undestand what you want to say from first time . In this problem you must to find are there possible roads in this graph to make all possible strings from 'A' and 'B' .
for example
the possible strings A,B,AB,BB . But in this graph you can't make "A" or "B" ,so answer is No
Damn. I implemented it in O(N^2) but didn't know how to speed it up. Should have noticed the subtask ;_;
Nevermind. I assumed we should split the sequence into intervals, what isn't true. I can't even solve it in O(n2).
My humble opinion: atcoder is bad in estimating problem difficulty.
My solution for 400: try all possible number of groups to divide elements into.
My solution for 700: assume that F(number_of_groups) is unimodal (being like: it is hard for me to tell why it is so, but a lot of random folks already solved the problem, so it is likely to be true), add ternary search to the solution for 400.
So in my case 400 was about naive solution :) And solution to get 700 is not just "let's fix bugs".
P.S. Cudos for this problem! My first thought was "Oh, something squared, should be yet another boring convex hull trick, I thought I'm solving AtCoder and not Codeforces — and the problems will be better than that".
Oh interesting, I didn't even realize it was unimodal. The way I implemented it, trying all possible number of groups to divide the elements into ran in time.
time.
Does that mean you can actually get this down to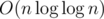 ?
?
What does "unimodal" mean here? Do you all mean bitonic (bitonicity)?
Yes, technically we mean bitonic.
Damn, prefix sums make life easier.
Thinking at least a bit makes life easier too :)
I'm not sure that it is unimodal :) And now after seeing how trivial intended solution is I doubt that my guess during the contest was correct, i.e. that ternary wasn't the default solution that other contestants used.
I wasn't sure about the unimodality, and still don't know how to prove it, (is it easy?) when I got the answer I had time only to code a brute force search on the number of groups or the ternary search I wasn't sure about, so went with the sure 400 points.
Is it so easy to see that the function is unimodal?
Edit: Just read your approach was different (and very cool :)) (the intended one)
How to solve B? Thanks to the following lemma:
The proof is obvious, so I skip it. This means that there is a simple DP[x] — minimum cost to collect the x left-most pieces of trash. DP[x] = minDP[y] + cost[y..x] where cost[y..x] is the cost to collect those pieces. We can calculate it using prefix sums to get O(n2) solutions. Then we can realize that it is always DP[x] = minDP[y] + f(y) + g(x) + h(y) * i(y) for some functions f, g, h, i, which we can evaluate in O(1) using prefix sums. The above can be optimised to using convex hull trick. A bit difficult for 700, but there were more solutions to C anyway. I have prewritten CHT, so it's not too much code. And then I got WA.
using convex hull trick. A bit difficult for 700, but there were more solutions to C anyway. I have prewritten CHT, so it's not too much code. And then I got WA.
Turns out that the lemma 1 is incorrect. Silly me. Well played, sugim48!
I used two unproven lemmas:
On round 1, the robot collects trashes at positions [n, n - a, n - 2a, n - 3a, ...], on round 2, the robot collects trashes at positions [n - 1, n - 1 - a, n - 1 - 2a, n - 1 - 3a, ...], and so on.
We can use ternary search to find the optimal value for a.
This was at least easy to code and was accepted.
Sorry for the delay of the editorial.
Meanwhile, some key insight: Suppose that a < b < c < d < e and we want to collect trashes on these positions in a single step. Then the minimum cost of walking is 11a + 9b + 7c + 5d + 5e.
Could you please upload editorials in which all English versions are available? I'm not sure if it is by accident or the translations are going to be added a bit later — current version doesn't have translations for A, B, C. And all I can say from Japanese versions is that my solutions for both B and C look different from ones in editorial :)
First lemma is obvious if you give it a few seconds of thinking. But I blindly assumed second one too.
Note that the cost of [n, n - a, n - 2a, n - 3a, ...] is 5xn + 5xn - a + 7xn - 2a + 9xn - 3a + 11xn - 4a.... The xi with the same coefficient form a consecutive interval and you can use prefix sum to get the answer for each group in O(1). Since there are ⌈ n / a⌉ groups, you can try all possible values of a in .
.
That's a very funny thing. This lemma was assumed with no further thinking about correctness by at least me, you and Errichto. It's obviously false and counterexample is obvious — it's better to collect (3, 1) in first run and (4, 2) in second run rather than (2, 1) in first run and (4, 3) in second one. I don't think it's because we are stupid, but because in easy tasks some experienced coders have habit of blindly matching very typical observations and patterns and keeping fingers crossed they are true without thinking if they are true. Because easy problems needs to have easy solution, right? So such assumption can't be false :P.
Lol, it's actually the opposite, for each i, all pieces of trash which are collected first in their journey form some interval, same for second, third, etc. Because, in each journey we pay 5xi1 + 5xi2 + 7xi3 + 9xi4 + ... + (2k + 3)xik + (k + 1)X, so for ij we save X - (2j - 2)xij energy. If we take some xi as j-th in some journey and some xk as l-th in other journey and xi < xk and j < l, then if we swapped them, the total energy will decrease. To guarantee that we can swap them, we should take adjacent xi and xk(we can always do that, because bubble sort works).
So the solution is to fix k and split trash into segments of size k, then i-th segment add to answer. It can be done in O(n / k), then overall complexity is
to answer. It can be done in O(n / k), then overall complexity is 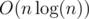 .
.
Lol, I know, read the last paragraph :)
It took me four WAs to realise what you're saying. Not my proudest moment.
In F, why can't we just consider every maximal common subgraph and greedily take vertices that are allowed to put in a good place? This approach passes samples but gets WA on systests.
try 1-2-3-4-5 3-1-2-4-5 the answer is 5.
Wow... So is it really possible to solve this problem if such mambo-jambos are possible :P? Can't be xD
Hint: the observation above is correct when the answer is not N.
Haha, yeah, it was my next guess that maybe it is correct after first step and we can consider n^2 first moves xD. As I explained in reply to majk's post — just guessing what kind of pattern may be applicable here without any thinking why :D. Does it fit in TL without some complexity improving observations?
How to check is there some cycle A - A - B - B - A - A... in problem C ? I tried dfs, with saving what letter is the next and parity of that letter from beginning of dfs, but I got WA at one testcase.
Call every vertex that has both an A-neighbor and a B-neighbor good. Then, for all the good vertices, you can check to see whether they have both a good A-neighbor and a good B-neighbor. If a vertex v was originally considered good, but does not have both a good A-neighbor and a good B-neighbor, then iterate through each of v's good neighbors u and remove v from u's good neighbor count. Then, add u to a queue if it also no longer has any more good A-neighbors and good B-neighbors. Keep doing this until your queue is empty, and then if there is a good cycle remaining, you're done.
Sorry if I was a bit unclear, I'll be writing a more thorough version on a comment above.
EDIT: Oh, I didn't realize there was a solution that just straight up finds such a cycle without any vertex marking or anything like that. Sorry for my misunderstanding.
how to solve C?
My solution is different:
Consider a node to be "dead" if it has no edges to other nodes labeled A or no edges to other nodes labeled B.
While there exists a dead node, remove it and all its edges from the graph. Answer is yes if and only if this process does not delete the whole graph.
B was too hard for B / F was too easy for F (I think E is harder) but it was a cool contest. C was very interesting!
Thank you for your partipation!
A and E were proposed by sugim48, B, C, D and F were proposed by me.
Full editorial is ready now.
The solution of problem D states:
"How can we make sure that ”max mod min” is a constant? One natural way is the following. First, paint a N × N board like a chessboard, as in the picture 1. Write arbitrary numbers on black cells. Then, on white cells, write ”The LCM of all neighboring black cells” plus one. This way, the value ”max mod min” is always 1."
I dont think it holds true. Consider the following case:
white | 6 | white | 10 | white
35 | white | 100 | white | 77
white | 143 | white | 39 | white
........................................
........................................
In this case,value in cell (2,2) will be equal to value in cell (2,4) which violates the restriction.
Though I still don't understand why summing them up won't provide any collisions...
You are multiplying them, not summing.
Lol. But then it should be product of four primes, no? Ahh, right, we use this trick to use small primes. I was stuck at the contest thinking that I must to use less than 4 primes >_<
You misunderstood the purpose of this excerpt. The only question that is answered by this paragraph is "How can we make sure that ”max mod min” is a constant?" and it answers it correctly. Getting rid of hypothetical collisions are addressed later on.