How do I calculate the length of the path to the farthest node for all nodes in a weighted tree?
Thanks in advance. :)
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | adamant | 164 |
| 2 | awoo | 164 |
| 4 | TheScrasse | 160 |
| 5 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | SecondThread | 150 |
| 7 | -is-this-fft- | 150 |
| 9 | pajenegod | 145 |
| 10 | BledDest | 144 |
| Name |
|---|



Let's make some vertex a root of the tree. Let dx, y be the length of the edge between verteces x and y.
Let fv be the maximal distance from vertex v to the vertex in its subtree. We will calcutate this value for all verteces using dfs:
Let gv be the maximal distance from vertex v to the vertex that is not in its subtree. We will calcutate this value for all verteces using dfs:
Then we will calculate ansv — answer to the problem. We will calcutate this value for all verteces:
It's a bit unclear what you are asking. Are you asking about the longest path from the root to any of the nodes, or are you asking about the longest path between any two vertices? Also, are any of the weights negative?
I was asking about the length of the path to the farthest vertex reachable for every node. And all weights are non negative.
Extremely sorry for the inconvenience.
No worries, I actually think I should have read it more carefully. In that case, you can use the fact that for all vertices, the farthest vertex will be the endpoint of a diameter of the tree. Thus, you can find the diameter with two DFS' in O(n) time, and calculate the distance from each endpoint of the diameter with another extra DFS.
Imagine you found a diameter of your tree. Let the endpoints be u and v.
Then we can prove that answer(x) = max(dist(u, x), dist(v, x)), where dist(a, b) is the distance between vertices a and b.
Then we simply need to find the diameter (2x DFS) and then find find the distances from u and v to all other vertices, which results in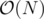 .
.