I need to solve the following task as a subtask of another problem. So I need your HELP.
I need a Data Structure that can do the following operations:
Add a pair of integers (x,y) in the Data Structure.
For a given pair (a,b) it will give me the count of the number of pairs (x,y) such that x<=a and y<=b.
Note: Maximum Time Complexity for both of the operations can be at most O(log n).
Trivia: (not for this problem) I am interested if there is a solution with erase operation.










This task can be solved online with O(log(n)^2) per query and O(log(n)) per update with merge sort tree. It's offline version has O(n*log(n)) solution for all queries, but as I can see you need to do it online.
Can you elaborate more about the online solution? And if you have time I want to learn about the offline solution too.
Notice that the problem is same as adding one to cell (x, y) and summing the rectangle (1, 1) → (a, b). If either one of them is negative you can just add some offset.
Now, if either one of x or y is bounded by M, then you can use Compressed 2D Binary Indexed Tree to get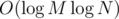 complexity, however with O(N + M) memory complexity. If M is too big, you can still do it in O(N) memory but that'll add another
complexity, however with O(N + M) memory complexity. If M is too big, you can still do it in O(N) memory but that'll add another 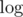 factor in time complexity (use map for those M ordered sets).
factor in time complexity (use map for those M ordered sets).
There is another solution, when both x and y is big, then you can adapt the solution of the problem "Game" from IOI 2013. That was basically updating an index on a grid, and finding gcd of a subgrid, but grid size can be 1018 × 1018. It has solution with complexity , and memory
, and memory 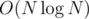 .
.
I think you can use binary partition here.
Let's have a data structure that can solve this problem: He have an array of pairs such that its sorted by the first element already and one kind of query : For a pair (a,b) count how many elements have x <= a and y <=b. We can solve this easy version with a binary search on index of bigger i such that the value is bigger than a and waveleet tree (i don't know how big the values can be, but i am assuming that they are big).
So we can turn the original problem in versions of this problem, lets make log(Q) buckets such that:
So now, in every bucket we maintain a vector of pairs such that they are sorted by the first value (x) and a data-structure that allow us to query (in such case, waveleet tree), if we have an query of type 2, we will pass for every bucket, in every bucket we will do as follow:
The answer will be the maximum of the answers in every bucket
For type one query we will do as follow:
Lets see the complexity for every query:
For the trivia part, i think you can refeer to this and keep tracking where every element is.
Árbol 2D, que funciona en O({log2}N) por query. No se me ocurre nada mejor que eso. Perdón.
About the online solution: At the beginning imagine you have infinite number of empty BST-s. When you add a pair (a, b), you insert b in the BST with index a. And you can keep a dynamic segment tree over all numbers. Let me explain it clear: in a node in the segment tree, which is responsible for [left; right], you store a BST with all the numbers from all the BST-s with indexes in the range [left; right]. Now I think that the adding of a pair is clear. And so is the erase (instead of inserting in the BST, you just erase). But the query seems a little problem. Let our query is (a, b). Then will ask the segment tree to find the number of elements smaller than b in the range [0; a]. So it is only left to find the number of elements smaller that b in a BST. I think that this is also clear. About the BST i recommend treap, but you can also use AVL or something else.