Всем привет.

Сегодня я расскажу об очередной суффиксной структуре данных. Насколько мне известно, ранее она не описывалась. Но даже если это не так, она кажется мне настолько простой для понимания, что в ее реализации трудно ошибиться. Надеюсь, вам тоже так покажется.

Эту структуру я обнаружил в попытках найти простое решения для задачи индексирования в реальном времени. В спортивном программировании алгоритмы реального времени вряд ли нужны, поэтому здесь мы будем спокойно пользоваться хэш-таблицами и амортизированными алгоритмами. Все фрагменты кода будут на языке Java.

Определения

Надеюсь, вы уже знакомы с терминологией строк. Несколько уточнений и определений:

• Суффикс строки ω называется "собственным", если он не равен самой ω. Например, пустая строка — собственный суффикс любой непустой строки; ω является наибольшим собственным суффиксом строки cω для любого символа c.
• Строка π имеет вхождение в ω, если π в ней содержится в качестве подстроки. У π может быть более одного вхождения в ω. Особенно нас интересует самое левое вхождение (leftmost occurrence, LMO). Например, самое левое вхождение пустой строки находится перед первым символом любой непустой строки.
• Все не самые левые вхождения будут называться повторами или повторными. Например, наибольший повторный суффикс (longest repeating suffix, LRS) строки ω всегда является ее собственным суффиксом; у пустой строки нет LRS.
• Симолы строк нумеруются с 1.

Структура данных

Структура строится в режиме онлайн. Для каждого префикса входной строки вычисляется наибольший повторный суффикс (точнее, его самое левое вхождение).

Самое левое вхождение описывается упорядоченной парой чисел: правый конец (включительно) и длина.

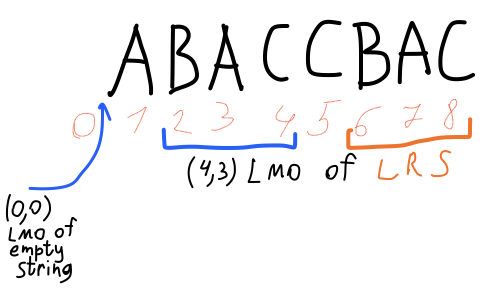
Всего в структуре три компонента:

1. Строка
2. Массив LRS, который хранит для каждого префикса строки самое левое вхождени LRS.
3. Хэш-таблица 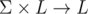, которая по LMO вхождения π и символу c выдает LMO вхождения π c (которое будем называть расширением π с помощью c).

Хэш-таблица хранит только нетривиальные расширения. (Расширение называется тривиальным, если оно получается простым инкрементом правого конца и длины.)

На джаве это выглядит так:

List<Character> text;
List<Lmo> lrs;
Map<Pair<Character, Lmo>, Lmo> extensions;

Операции над LMO

Это не обязательно, но мы определим символ null равным любому другому символу. Позже, это позволит нам избежать разбора случаев в алгоритме построения.

boolean isNext(Character c) {
    Character next = text.get(rightEnd + 1);
    return next == null || next.equals(c);
}

Есть два способа получить расширение LMO: тривиальное и из таблицы расширений.

boolean hasExtension(Character c) {
    return isNext(c) || extensions.containsKey(Pair.of(c, this));
}

Если следующий символ равен c, то тривиальное расширение является самым левым. Доказательство: если бы самое левое расширение было в другом месте, то это противоречило бы тому, что исходное вхождение — самое левое.

Lmo extend(Character c) {
    return isNext(c)
                ? new Lmo(rightEnd + 1, length + 1)
                : extensions.get(Pair.of(c, this));
}

Для наибольшего собственного суффикса LMO тоже есть два случая: тривиальный и когда он совпадает с соответствующим LRS. В последнем случае нужно взять его LMO. Доказательство: по определению, LRS — это повтор, а значит не может быть LMO. Тривиальный случай доказывается от противного.

Lmo lrs() {
    return lrs.get(rightEnd);
}

Lmo longestProperSuffix() {
    return length - 1 == lrs().length
            ? lrs()
            : new Lmo(rightEnd, length - 1);
}

Вычисление LRS и его LMO

Если мы реализуем класс Lmo со всеми операциями и методами для хэш-таблиц, мы сможем приступить к построению массива LRS.

Алгоритм принадлежит тому же семейству, что и алгоритмы Кнута, Морриса, Пратта, Укконена и droptable. Эти алгоритмы онлайновые и поддерживают наибольший суффикс, для которого выполняется некоторое свойство. Наш случай наиболее похож на алгоритм Укконена: мы поддерживаем наибольший суффикс, который уже встречался ранее.

Мы берем LMO наибольшего повторного суффикса и пытаемся расширить его символом c. Если не получается, мы сохраняем новый LMO в таблицу, а затем пытаемся повторить то же самое с более коротким суффиксом. Алгоритм работает за амортизированное (ожидаемое, из-за хэш-таблицы) O(1) по той же причине, что и остальные подобные алгоритмы.

Как я сказал ранее, у пустой строки нет LRS. Чтобы избежать разбора этого случая, используем стандартный трюк: пусть у пустой строки есть такой искусственный LRS, что

• Его можно расширить любым символом.
• Его расширением является пустая строка.

Это достигается за счет того, что мы помещаем null в нулевой символ строки, а в нулевой элемент LRS-массива помещаем ( - 1,  - 1).

Алгоритм для вычисления LRS после добавления символа c выглядит буквально так:

Lmo longest = lrs.get(lastIndex);

while (!longest.hasExtension(c))
{
    extensions.put
    (
        Pair.of(c, longest),
        new Lmo(lastIndex + 1, longest.length + 1)
    );

    longest = longest.longestProperSuffix();
}

longest = longest.extend(c);

class LrsArray {
    List<Character> text = arrayList(null);
    List<Lmo> lrs = arrayList(new Lmo(-1, -1));
    Map<Pair<Character, Lmo>, Lmo> extensions = new HashMap<>();

    Lmo append(Character c) {
        text.add(c);
        int lastIndex = lrs.size() - 1;

        Lmo longest = lrs.get(lastIndex);

        while (!longest.hasExtension(c))
        {
            extensions.put
                (
                    Pair.of(c, longest),
                    new Lmo(lastIndex + 1, longest.length + 1)
                );

            longest = longest.longestProperSuffix();
        }

        longest = longest.extend(c);

        lrs.add(longest);
        return longest;
    }

    class Lmo {
        final int rightEnd;
        final int length;

        boolean isNext(Character c) {
            Character next = text.get(rightEnd + 1);
            return next == null || next.equals(c);
        }

        boolean hasExtension(Character c) {
            return isNext(c) || extensions.containsKey(Pair.of(c, this));
        }

        Lmo extend(Character c) {
            return isNext(c)
                    ? new Lmo(rightEnd + 1, length + 1)
                    : extensions.get(Pair.of(c, this));
        }

        Lmo lrs() {
            return lrs.get(rightEnd);
        }

        Lmo longestProperSuffix() {
            return length - 1 == lrs().length
                    ? lrs()
                    : new Lmo(rightEnd, length - 1);
        }
    }
}

Теперь рассмотрим несколько задач, которые можно решить этой суффиксной структурой.

Количество различных подстрок

Если после добавления очередного символа длина строки равна n, то значит у нас появилось n новых подстрок, за исключением тех, что повторились. Тогда полное количество различных подстрок для строки длины n равно

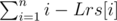
Куда сдать: Тимус. 1590. Шифр Бэкона

Наибольшая общая подстрока

Сначала добавляем символы первой строки, затем специальный символ-разделитель. Затем добавляем символы второй строки, параллельно поддерживая максимальный LRS. И надо не забыть проигнорировать те LRS, LMO которых находится внутри второй строки.

Куда сдать: Тимус. 1517. Свобода выбора

Количество повторов

Массив LRS можно обработать, чтобы построить дерево повторов (перевернув направление ссылок LMO). Это дерево нужно обойти, чтобы узнать количества повторов для подстрок возможно различных длин. Затем нужно учесть, что если несколько повторов с одним и тем же правым концом имеют разную длину, то более короткие являются подповторами более длинных.

Куда сдать: 802I - Ложные Новости (сложная). Совет: сделайте Lmo с интерфейсом Comparable.

Упорядоченный список суффиксов в режиме онлайн (справа налево)

Не могу сказать, зачем это нужно, но тем не менее.

Если посмотреть на строку справа налево, то все LRS превращаются в LCP. Это значит, что алгоритм для каждого нового суффикса дает соседа и способ сравниться с ним за константу.

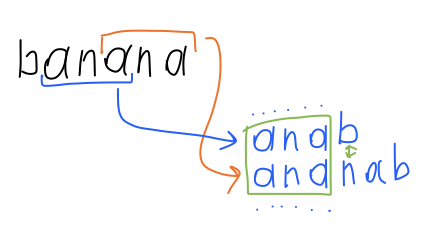
Суффикс, который нам сообщает LRS, может оказаться достаточно далеко от того места, куда его нужно вставить (на столько, сколько различных букв в алфавите). Чтобы найти самого близкого соседа нужно:

• либо использовать список с произвольным доступом + бинарный поиск,
• либо заполнить еще одну таблицу , которая для каждого LMO π и символа c говорит, где найти суффикс вида α cπ. Ключи этой таблицы должны быть упорядочены, чтобы можно было найти ближайший к c.