I tried all day to solve this problem:
Bring an integer N to 1 doing one of these operations each step: N /= 3; N /= 2; N -= 1;
1 <= N <= 1e9
output = minimum number of steps.
This is the function I wrote:
int solve(int n) {
if (n == 1) return 0;
if (n == 2) return 1;
if (n % 3 == 0) {
if (n % 2 == 0) return solve(n / 3) + 1;
else return min(solve(n / 3), solve((n - 1) / 2) + 1) + 1;
}
if (n % 2 == 0) {
if ((n - 1) % 3 == 0) return min(solve((n - 1) / 3) + 1, solve(n / 2)) + 1;
else return min(solve((n - 2) / 3) + 2, solve(n / 2)) + 1;
}
if ((n - 1) % 3 == 0) return min(solve((n - 1) / 3), solve((n - 1) / 2)) + 2;
return min(solve((n - 2) / 3) + 1, solve((n - 1) / 2)) + 2 ;
}
I think the complexity of my solution is linear and the answer it gives should be correct but I'm not sure.
Can you help me find the best solution?










Let's find answer for all n <= 10 ^ 7 = M, it can be done with simple dp. Then how to solve it for n > M? As we know ans[n] = min(ans[n / 2], ans[n / 3], ans[n — 1]) Well, let's run recursion, if n <= M: return dp[n]; else: we use our formula
But is still does not work fast, because we will find answer for n, n — 1, n — 2, ... M + 1. Notice that there is no point in decreasing n by 1 3 or more times because instead n -> n — 1 -> n — 2 -> (n — 2) / 2 we do n -> n / 2 -> n / 2 — 1, case when we divide n by 3 after several decreasing by 1 is the similar
Now let's run our recursion again, but in recursion we will check that we don't substract 1 3 or more times. And this solution should works fast
Yes this is a lot faster than without dp, can you explain briefly the dp algorithm done in linear time?
EDIT: Nvm I think I got it, it is really simple indeed
If we let R(N) be the answer for N, then:
The time complexity recurrence is $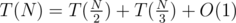 and this should be fast enough even without memoization. We can analyze it with the Akra-Bazzi method to find that the actual complexity is O(N0.79).
and this should be fast enough even without memoization. We can analyze it with the Akra-Bazzi method to find that the actual complexity is O(N0.79).
This is exactly what I did, but I realized it after I coded that mess.