Hi everyone,
I am learning this relatively new data structure with a Kattis problem called Palindromes. In this problem, we are given a string and multiple [l, r] segments and must find the number of palindromic substrings in each segment. The number of queries and length of the string are all 10^5. My question is: Is it possible to achieve this with Palindromic Tree and if yes, how can we do that?
I am not absolutely sure if this DS can handle such problems, but at least, I know that for [1, r] segments, it is possible, Is this variant possible? If it is possible, please give me your guidance.
Thank you very much :). Happy Coding










Help :'(, please.
It feels like you could combine palindromic tree with Mo's algorithm.
Ignore, Palindromic tree doesn't easily support removing from front
I'm not sure about how palindromic tree works but Mo can work with only adding to the left and to the right operations.
That's true, I once prepared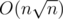 solution for similar problem (about number of distinct palindromic substrings) using Mo-like sqrt-decomposition. It briefly mentioned in this article and droptable posted his
solution for similar problem (about number of distinct palindromic substrings) using Mo-like sqrt-decomposition. It briefly mentioned in this article and droptable posted his  per query solution here.
per query solution here.
Mo's works with only adding to the left and right (no removing)? How do you sort your queries?
You don't really sort the queries. We create buckets and each bucket will have the queries with left end in it. Also if queryR — queryL <
buckets and each bucket will have the queries with left end in it. Also if queryR — queryL <  we will solve the query separately in O(queryR — queryL).
we will solve the query separately in O(queryR — queryL).
Now we will solve each bucket. We sort the queries in the bucket by their R and we keep two pointers, pointing to the current L and R end. Initially pL = pR = end of the bucket. We move the right pointer like in the standard Mo. The only difference is that you will only move it to the right. For the left pointer it's a bit different. Your structure should be persistent (you should be able to rollback it). After fixing the right end of the current query, you go from the current pL to the needed position. This is done only by moving the pointer to the left. When both ends are fixed, you answer the query. Now the only left part is to undo this left movement simply set pL = end of bucket again and go to the corresponding rollback state.
By Palindromic Tree, do you mean Eertree?
I'll think about it for a while and get back to you.
Yup, Eertree = Palindromic Tree, but I find the later more meaningful :).
It's been asked and answered a few days go here: click me
What a coincident :o ! Thank you. I never ever thought of using Manacher like that.
But is it solvable with Palindromic Tree? Well, I mean, I am learning PalTree, so I want to find more applications for it. :), but sure, the approach seems to solve my example problem and I will implement it :).