Rating changes for last rounds are temporarily rolled back. They will be returned soon. ×

Djok216's blog

Grand Prix of Siberia
By Djok216, history, 5 years ago, translation, In English

Let's discuss problems.

How to solve 6, 11, 12?

  • Vote: I like it
  • +41
  • Vote: I do not like it

»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why the problem statements are not available? I can only see the samples and constraints but there's no statements.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    On the upper right side there is a download sign. click there.

    → Reply
»
5 years ago, # |
  Vote: I like it +13 Vote: I do not like it

How to solve 7?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    First, you delete cells with weapons and the problem is reduced to defining whether there is a monster in the component with the starting cell.

    You can implement this using dynamic connectivity

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +29 Vote: I do not like it

    In case you seek an answer in closed form...

    Maintain a DSU of all cells, initially fully isolated. First, merge all adjacent cells which never contain a weapon. After that you need to implement a recursive function solve(L, R), which solves all object sets in range from L to R. Here is how this function works with DSU:

    • Precondition: All cells are merged in DSU, except for those cells which contain a weapon in at least on object set from the range [L, R).
    • Postcondition: After the call, DSU is in the same state as it was before the call.

    And here is its pseudocode:

    1. If the range [L, R) contains only one set, check in DSU if the player is in same component with any monster of the set. Print this answer and exit.
    2. Split the range evenly into two subranges [L, M) and [M, R).
    3. Merge the cells which never contain weapon in [L, M) but which do sometimes contain weapon in [M, R).
    4. Call solve(L, M) recursively.
    5. Rollback the DSU to the state it had just before point 3.
    6. Merge the cells which never contain weapon in [M, R) but which do sometimes contain weapon in [L, M).
    7. Call solve(M, R) recursively.
    8. Rollback the DSU to the state it had just before point 6.

    This solution has to iterate through each weapon at most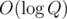 times, potentially doing O(1) DSU operations per weapon. You need to implement DSU with rollbacks, for which you absolutely have to implement proper union-by-size or union-by-rank heuristic (just choosing randomly the merge direction does not suffice). With such heuristic, every single DSU operation takes in worst case, so the total work time is about .

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

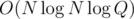      Our team got accepted (in Yandex contest upsolving) solution based on DSU without rank heuristics, just paths compression. Strange fact, this solution works faster than solution that uses both heuristics:

      1. https://pastebin.com/SsQ765jB — 3413 ms with both heuristics
      2. https://pastebin.com/Vi4h4zaD — 2884 ms with just paths compression
      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Sad fact: there is no counterexample for your solution in our testset. I believe there exists one if you search hard enough.

        If you want some fun, change parent[u] = v; to parent[v] = u; in your code and resubmit =)

        → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What about 5?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    The problem is equivalent to finding the diameter of a graph, so our team wrote a bfs from every node using bitsets, final complexity is something like O(N3 / 32).

    p.s. the answer are layer from a bfs tree if we start from vertex X and there exists vertex Y such that Path(X, Y) is the diameter of the graph.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Did you implement your own bitset? Stl bitset does not give you list of 1s, does it? (I just came to know about _Find_First and _Find_Next, did you use it?) For some reason they are not documented in the cppreference/cplusplus sites.

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Yes, we used it (bitset with _Find_Next). Without _Find_next we got TLE.

        → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +21 Vote: I do not like it

        The fastest way to iterate over all set bits in a handmade bitset is to use x86 bsr instruction:

            while (mask) {
        unsigned long msb = mask & (-int32_t(mask));
        mask ^= msb;
        unsigned long x = 0;
        _BitScanReverse(&x, msb);   //you need another intrinsic on GCC
        ... // x is index of bit
    }
        → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        I used this code:

        bitset<maxn+100> bits = ...
uint64_t *ptr = reinterpret_cast<uint64_t*>(&bits);
for(int i = 0; i <= maxn / 64; ++i) {
    if (*ptr) {
        for(int j = 0; j < 64; ++j)
            if ((*ptr) & (1uLL << j)) {
                ...
            }
    }
    ++ptr;
}
        → Reply
»
5 years ago, # |
  Vote: I like it +54 Vote: I do not like it

6 and 12 are very nice.

6: Construct a graph with 2n vertices. The first n vertices corresponds t "I'm at i and the tank is empty" and the last n vertices correspond to "I'm at i and the tank is full".

Transitions:

  • Empty i to Full i. (Fill at i)

  • Empty i to Empty j. (Fill at i)

  • Full i to Full j. (Fill at j)

  • Full i to Empty k via j. (Fill at j)

12: First let's count the number of subsequences of a given string s. In the increasing order of i, for the prefix s[0: i], we keep the following 27 values:

  • The number of subsequences of the prefix that ends with 'a'.

  • Similar values for 'b', 'c', ..., 'z'.

  • The total number of subsequences of the prefix (including the empty string).

The most important observation is that, when we are only interested in the parities, we just permute these values. For example, when we append 'a' to the prefix, the values "The number of subsequences of the prefix that ends with 'a'" and "The total number of subsequences of the prefix" are swapped and the other values are unchanged. The remaining part is easy.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You mean- swapped and parity changed both of them, right?

    Our next part was, dp of bitmask(2^20) * loop-to-find-zero-bits * 53 (which character we are at and what parity). Is there easier solution for this part?

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      No, they are just swapped and the parity doesn't change. (Note that I counted the empty string in the 27th value.)

      → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +48 Vote: I do not like it

    rng_58 called my problem a nice one. I achieved everything as a problemsetter!

    → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What is time complexity of solution? I've tried O(N * 27 * 2^N). But it didn't pass TL test 12.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Making it iterative worked for me (my one was N*53*2^N)

      → Reply
»
5 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve 13? Can't pass tc #25.

→ Reply
»
5 years ago, # |
  Vote: I like it +1 Vote: I do not like it

How to solve 4?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    The code is wrong because of  < N conditions in every loop. To repair that you have to fix w = N and perform other two loops from 1 to N. After that, you have to do the same with u = N and v = N. Also, you should "apply" this two times.

    Here is the function you have to apply two times in order to fix the code from the problem.

    → Reply
»
5 years ago, # |
  Vote: I like it +21 Vote: I do not like it

How to solve 2?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Ternary search over the angle of acceleration and find minimum a to get to the point (d, w / 2). There is a tricky case when angle is close to π, you would not come to that point, so check whether your function returned a right answer. Also, we considered the case when it is optimal to make a full-stop before the wall.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Why does ternary search give necessary precision? Ternary search is quite obvious, but I thought that the constraint 10 - 10 has been specially set in order to break such solutions.

      → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We have pure analytic solution — by some tricks with formulas and find min(max) with derivatives. No any binary (or ternary) search.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      we had an analytic solution with the assumption that a is fixed. How to prove that it doesn't make sense to change it?

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it +31 Vote: I do not like it

        Let a(t) be acceleration depending on time. For simplicity, switch to coordinate system of the priest (but with car starting at origin).

        Suppose that the car evades the priest at point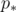 at time . Then vector 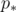is the integral of 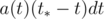over 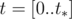. Then you can replace acceleration a(t) with constant acceleration a0, which is a weighted average of a(t) over 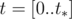with being the weight function. If you do such replacement, you will still get to the same point 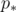by time evading the priest, but using constant acceleration vector this time. And by convexity, this average acceleration a0 will have magnitude less than the maximum magnitude of a(t).

        → Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 3   Vote: I like it +13 Vote: I do not like it

    God given fact: it's sufficient to use constant acceleration.

    Let's say that our car is in coordinates (0, 0) and priest is in coordinates ( - w / 2, d) and (w / 2, d). Now we will either end up in (w / 2, d) or in (0, d). In first case we deal with the optimization problem:

    Let's rewrite this as a function of t without additional boundaries:

    It has extremal values when the derivative is zero:





    Looking at the graphs for some partial cases we may say that we should always take minus to get minimum value. And if for discriminant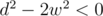 , you should always consider only second option.

    In the second case you may find out that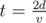 and .

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

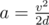How about the remainings? 3, 7, 8, 9, 11?

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Hint in 8: read the problem statement

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      can you explain this part in more detail, please?

      → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      In problem 8, it is really written in the statement what should be done. The problem is that implementation is a bit technical and scary. But it is rather easy to do with proper box-oriented mindset.

      1. Notice that every topological element is a box geometrically, although the boxes of vertices, edges and faces have different dimension (dimension is how many coordinate intervals have R > L).
      2. You can easily generate all 26 topological elements by doing triple loop: xc = -1, 0, 1; yc = -1, 0, 1; zc = -1, 0, 1. The code xc = -1 means that X_interval is [Lx, Lx], code 0 means set X_interval to [Lx, Rx], and code 1 means X_interval = [Rx, Rx]. Of course, the case xc=yc=zc=0 must be excluded, since it gives us the unwanted 27-th element.
      3. Now that you have all topo elements, pairwise intersect them. This is done trivially by intersecting boxes, regardless of their types. Since boxes are closed, while topologies exclude boundary, you have to be careful to not add same intersection element many times. This can be achieved e.g. by having a set where you put all already found intersection elements.
      4. Perform a double loop over intersection elements to find all links/connections. Two intersection elements are connected iff their boxes have common point, so the check is trivial.
      5. Print out whatever this long output format description wants from you, check that you pass sample, submit and get accepted.
      → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +28 Vote: I do not like it

    The problem 9 is about shortest path on sphere. I guess the same problem is known on plane, and on sphere the solution does not change much, except for geometrical primitives. It is clear that the optimal route should go along boundaries of the spots, and also sometimes from spot to spot directly. When you leave a spot boundary, you should continue moving tangentially in optimal case, and when you get onto a spot boundary, you should do so tangentially too. So the problem can be solved by building a graph from all the critical points and running Dijkstra in it.

    In a fully analytic solution, start and end points may be considered as two special spots of zero radius. Then you need to implement the following primitives:

    1. Find four common tangent lines for two specified spots.
    2. Check if a direct line from one point to another intersects a given spot.
    3. Sort all critical points on the boundary of a given spot by polar angle.
    4. Check if an arc on the spot boundary intersects a given other spot.

    A lot of problems on sphere become easier if you consider three-dimensional objects instead. Imagine that a spot is a cone with vertex at origin, and every unbounded direct line is a plane passing through origin. The problem 1 (being perhaps the hardest one) then is equivalent to finding a plane passing through origin, which is tangent to two given cones with vertex at origin. A plane is determined by normal vector N, so it can be determined from:

    Here Ci and di are parameters of the ith cone. Three components of N are unknowns here, so this equation can be solved. In fact, it can be thought of as an intersection of two planes and a unit sphere (if vector N is considered a point in space).

    To solve the problem 3, you can define a local coordinate system with Z axis being the center axis of the cone, then sort points by atan2 of their local X,Y coordinates. Problems 2 and 4 can be solved like this: check if endpoints of the path are inside the cone, then find a critical point on the path by projecting something onto it, and check also if this critical point is inside the cone.

    Trying to solve this problem during the contest is indeed a bad idea, but it should be fun to write after the contest, given that you like geometric problems =)

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Thank you for your notes. It was interesting to see how imagining the problem in terms of cone and plane can ease lot of works. Can you please elaborate a bit on "it can be thought of as an intersection of two planes and a unit sphere".

      → Reply
      • »
        »
        »
        »
        5 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Only normal N is unknown in the equation system, which has three components (x, y, z). Now imagine the 3D space of all possible normals: each value of x, y, z corresponds to a point in such space.

        The first two equations are linear/affine with respect to N, so each of them defines a plane in the space. These planes do not pass through origin, because the right side is usually non-zero. The last equation says x2 + y2 + z2 = 1, which is the equation of unit sphere centered at origin.

        So in order to solve the equation you can first intersect the planes (C1, d1) and (C2, d2) in this 3D space, getting a line as a result. Direction of this line would be D = [C1 × C2], but offset is much harder to get. I represented offset as , where 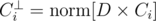is a normal vector to Ci in the L(C1, C2) plane, and α and β being unknown parameters. Then put this offset into the linear equations replacing N, which allows to obtain unknown parameters easily. Not very straightforward way, but allows to avoid special cases =)

        When you have the line equation in parametric form, just perform a line-sphere intersection (reduced to quadratic equation as usual), and you'll get two values of N which satisfy the equation system.

        → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    For 3, you don't really need to play minesweeper. There are less than 10000 possible seeds S, so you can generate the field for all of them.

    At each point, you choose a square that is least likely to contain a mine (based on the possible fields) and then remove all fields that don't match the response you get. (Just checking whether you get 'Empty' or 'Boom' was sufficient to get OK, but that fails occasionally on cases with 200 mines.)

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there anyone who got problem 7 AC using sqrt-decomposition over queries with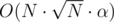 complexity which seems to have running time close to 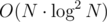solution under these constraints?

We had an idea to decompose all queries into blocks each block having at least one query and total amount of different weapon cells in single block is not greater than . But we failed to implement this properly in contest time.

→ Reply