W--o_o--W's blog

Tree Path problem
By W--o_o--W, history, 5 years ago, In English

Hello,

I came up with the following problem but I'm not sure if it is possible to solve it in less than O(n2), any ideas?

You are given a weighted tree with n nodes and you are allowed to swap the costs (1 ≤ cost ≤ n) of two edges at most once such that the sum of all paths in the tree is maximum.

  • Vote: I like it
  • +52
  • Vote: I do not like it

»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

you can preprocess for each edge the number of paths that it belongs to ( with simple dfs ) and then for each edge swap it with another edge and see how the total sum changes : sum = max(sum ,original_sum + (cost[edge1] — cost[edge2)] * (paths[edge2] -paths[edges1] ) )

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

does bruteforcian ternary count ?

→ Reply
»
5 years ago, # |
  Vote: I like it +51 Vote: I do not like it

I'm not sure this is correct and can't even implement this solution, but I'll write it here anyway.

Suppose that for each edge x, we have its cost px and the number of paths containing it cx.

For each edge a, we must find an optimal edge b to swap. The current contribution of both edges is pa * ca + pb * cb and after the swap, they will contribute with pa * cb + pb * ca.

Therefore, if we swap a and b, we will add pa * cb + pb * ca - pa * ca - pb * cb to the sum of paths and minimizing this sum will give us the answer.

So, for a fixed a, we can remove pa * ca from what we are trying to minimize, since this is constant.

Now, for each edge b, create a 3D point with coordinates (cb, pb,  - pb * cb). Let's call this set of points S.

Now, for each edge a, consider the 3D point (pa, ca, 1). The contribution of swapping a and b is exactly  - pa * ca + the dot product between this 3D point and the one corresponding to b in S.

Now, the best b for each a must lie on the convex hull of S. More specifically, since the geometric figure of the points with the same dot product is a plane, the exact point can be found with a query of closest point from some infinitely far point (sphere approximates plane). You can have a KD-tree for this.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    Thanks for you , it is tricky solution and I can't implement it , but I think it's always get the right answer .

    → Reply
  • »
    »
    5 years ago, # ^ |
    ← Rev. 5   Vote: I like it +11 Vote: I do not like it

    other idea:

    Let the point be of the form (ca, -pa). You need the maximum-area square ABCD formed with B and C from the original set of points

    A -- B

    |.......|

    C -- D

    this is not-exact solution:

    traverse the set of points with usual cmp, Let the last point checked (a,b) and the current point traversed (x,y).You need to update all points in the X component: for each x set it to x_i+x-a. In addition, change temporarily all points in the Y component from y to y_i+y-b. You finally notice that the solution is max(x_j*y_j) for all y_j in <-oo,y_i]. For a better performance, you can use max(exp(log(x_j*y_j))), so, you need to compute log(x_i) + log(y_i) efficiently. You can compute this using taylor series with ~ 50 terms and a fenwick tree.

    O(nlogn*50)

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      a = max(x_i), b = max(y_i)

      → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      As skywalkert mentioned above, this reduction is exactly World Finals 2017 D and it can be solved in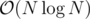 with divide and conquer.

      → Reply