Tutorial is loading...
Author, preparation: KAN.
Tutorial is loading...
Author, preparation: cdkrot.
Tutorial is loading...
Author, preparation: KAN.
Tutorial is loading...
Author, preparation: KAN.
Tutorial is loading...
Authors: MikeMirzayanov, cdkrot, preparation: cdkrot.
Tutorial is loading...
Author, preparation: Neon.
Tutorial is loading...
Author, preparation: KAN.
Tutorial is loading...
Author KAN, preparation: KAN, 300iq.
Huge thanks to cdkrot and 300iq for discussing the problems and general invaluable help in preparation!











Isn't the statement of C clear? "the other team must choose the other one on its turn", I didn't think "the other must choose immediately".
I found that confusing too & I discovered that I was misunderstanding the problem until I read the tutorial! :(
E) Haha — very funny...
There is a better solution for B — with O(m) time :)
I have it :) 46223705
Bro can u explain how are you able to calculate no i*i % m = k for a particular val
In addition to provided solution:
Instead of looping for every pair, you can loop through one dimension (loop through i^2) and calculate a vector which stores how many values mod m are equal to the index ( for i = 1 to m: vector_i[i^i mod m] ++ ). After this, do it for the other dimension (vector_j), and then sum all the products where indices give m when summed (for i = 1 to m: sum += vector_i[i] * vector_j[m-i]). Another note, since we are working with a square, vector_i and vector_j are in fact the same, so you need just one array.
O(m) solution for B https://codeforces.com/contest/1056/submission/46435129
Very fast edutorial, thanks a lot for a contest !
Edutorial is much better word than editorial.
Why set intersection in A problem doesn’t work?
it should and it does :) 46211365
How does persistent treap solve G?
My solution uses a persistent randomized BBST which is rebuilt whenever the depth becomes too large. I don't actually know why it works though ...
46228890
Why this code got accept? Very strange.
I am dumb. Can anybody tell me in problem E how can we check for a particular length, say l, of r0 the corresponding string formed exactly matches string t in O(|s|) time.
For each digit in s, compute the hash of the corresponding segment in t. Then compare the hashes.
To achieve O(s) complexity you need to compute hashes in O(1). Check out the section "Fast hash calculation of substrings of given string" in String Hashing.
Do we have to pray to many hash god that collisions don't happen, that is if collisions happen could it lead to incorrect output?
If you know a little bit theory, it's possible to prove that hashes work correctly with some reasonable probability (which depends on the number of operations and modulo)
At first, I used unsigned long long value for base and nothing define for mod value. as we know, in unsigned operation it works on modulo by 2^64. By this hashing approach, I got wrong answer in test 17. After this, I used a int base and 10^9 + 7 for mod. but it passes. As per I know, unsigned hashing is more secure than other where less collision is occur. If I am worng, please describe my above two process. Thanks in Advance.
No, you are wrong. Hashing with 264 is pretty bad.
Delete this
It doesn't say that the interactive took 13. That last line is both your output and the input. The problem is you took 3 instead of 32. It even says that in the comment
has been removed
problem G, second approach is very weird. let C[i]=exit station's index when start index is i and start t is n-1. If we do i=C[i] and check visit[i]=true recursively, at some time, C[i] is already visited. Let this time = cyc[i]. I can find a simple rule of max(cyc[i]). It is updated only n=2^k , m=1 or n-1. And max(cyc[i]) is:
n=8192 : max(cyc[i])=141, n=16384 : max(cyc[i])=188, n=32768 : max(cyc[i])=342, n=65536 : max(cyc[i])=475.
Although start t!=n-1 and just repeat (go next station use following algorithm ,t--) n times, we can gain similar value. So this code can accept! (because time complexity is O(475n))
But I can't prove this rule. Why max(cyc[i]) is very small? It seem weird.
My intuition is as follows. Perhaps a more fitting term would be a mumbo-jumbo hunch.
Renumber the stations such that 0 is the last red station and consider the last k steps, where k ≤ min(N - M, M). The process does something like this:
Looks familiar? Yes, this is a greedy solution to 2-PARTITION. It is incorrect in the general case, but works quite well in practice if the item sizes are well behaved. In particular, it will return a value close to zero if the ratio of consecutive elements is not too large and there are enough elements. If M is not very close to either 0 or N, this will return a value close to zero, and it will cycle very fast (like in 2-3 steps when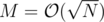 ).
).
What if, on the other hand, M is very small, say M = 1? Then I would be inclined to say that the amount by which you move counter-clockwise behaves like a random variable. If you move by the same amount twice, it means that You cycled. Due to birthday paradox, this occurs once in every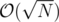 iterations. Your 475 looks quite close to
iterations. Your 475 looks quite close to 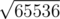 .
.
Don't be mad at me. Much smarter and more educated people than me have looked at Pollard-Rho for considerable amount of time and failed to produce anything substantially better than this bullshit.
Hi, I have a question, I still don't understand why you need to repeat the
t--algorithmntimes. Will you help me and clarify that part a bit? Thanks.Oh, is it because u want to restrict the time deduction to be a multiple of
n?Can you explain me please how to count the number of pairs in the problem B satisfying the condition (x^2 + y^2) mod m = 0 ?
The n*n matrix of (x^2+y^2) mod m is periodic & can be constructed from a matrix of size at most m*m, so 1000*1000 = 10^6 iterations at most.
It's due to the fact that for x,y <= m if (x^2+y^2) is divisible by m than ((x+m)^2+y^2) is also divisible by m because ((x+m)^2+y^2) = (x^2+y^2)+(2*m*x+m^2) = (x^2+y^2)+m*(2*x+m).
The first part is already divisible by m and the second is clearly divisible by m & the same thing goes for y so coordinates (x+m, y) & (x, y+m) are to be counted if they are in n*n.
Here is a picture that explains when n > m since n <= m is too easy. The total answer will be blue (n/m)^2 + green*2 + red.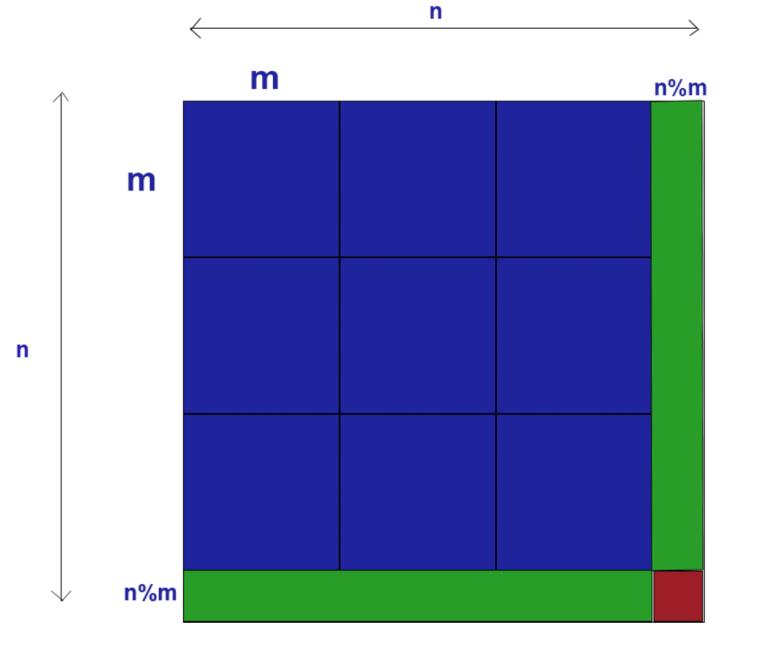
For problem F, is it possible to rigorously prove that it's always optimal to solve them from the hardest one to the easiest one? I see that it's intuitive for cases where the difficulties of the problems are spaced out enough (you only have to train once in that case).
This is the rearrangement inequality: https://artofproblemsolving.com/wiki/index.php?title=Rearrangement_Inequality
Let the difficulties of the problems be d1, d2, ..., dk in increasing order. We have factors of 1 / .9, 1 / .92, 1 / .93, ..., 1 / .9k and want to pair each di to a factor then add them up. You should put the highest di with the lowest 1 / .9i because you want to minimize its contribution to the total sum. Similarly, you should put the lowest di with the highest 1 / .9i because you want the small difficulty problems to count the most. So the smallest possible sum is d1 / .9k + d2 / .9k - 1 + ... + dk / .9.
Even though for fixed problems set it's optimal to solve in decreasing order, it doesn't help to find out how to fill dp x,k discussed in solution. 0 <= k <= 100 — number of tasks, 0 <= x <= 1000 — total score, total 10^5 "cells" and you need to fill them fast. also, nothing said about relationships in this dp and how to make sure that you don't pick any task twice. If you assume that "solve in same order" means that you should allow tasks one by one same as for knapsack problem, then it means that you should try to add current task for all known "solutions". This leads to for loop over n tasks, and then for loop over whole dp: 100*10^5.
I had other idea in my mind, but for some reason it fails on third test. I think I have proof of it, maybe I'm wrong. Anyway, I just say once again: provided solution doesn't help me.
This solution: tc*(n*n*(10*n)) works. Sad. I thought there should be something harder. My tc*n*(10*n) solution doesn't work. Looks like there is counterexample.
in B question i get the loop part but not able to understand how we are counting inside loop like the expression ((n-i)/m)*((n-j)/m) can someone expalin this to me
if x & y satisfy the condition then xdash = x + pm and ydash = y + qm will also satisfy the condition.
xdash <= n
x + pm <= n
pm <= n-x
p <= (n-x)/m
Same for q. Total number can be get by multiplication property of combinations.
For problem G, I'm so dumb that I can't understand how to compute "for each station the station you will end up after that large step" by treap or splay. Who can give me an example?
Does anyone know of a good resource for learning the "strong" approach to G with a persistent treap?
Yeah, same question. Someone please explain. ._.
Also to saketh.
I don't know what you mean by "learning", but here is my original solution to that problem: 55510205, if that helps.
in 1056E(check transcription) how we can check a pair(r0,r1) in |s| time , according to me it should be |t|, to check whether a particular pair of length (of string '0' and of string '1') is possible or not i need to cross through string t isn't it, please tell if you have done this
.
1056C-Pick Heroes https://codeforces.com/contest/1056/submission/83133126 please anyone help..why am i getting wrong answer