I can convert some simple recurrence relation to a mathematical formula.
Example: F(n) = n + F(n-1), if n > 0 and F(0) = 0; This recurrence relation can be converted into the formula: F(n) = (n*(n+1))/2
But for many other recurrence relations I am unable to do so.
Example: Lets consider the fibonacci sequence. F(n) = F(n-1) + F(n-2), if n > 1 and F(0) = 0, F(1) = 1; I tried hard to convert this recurrence relation to a formula, but failed.
So, my question is it actually possible to convert every recurrence relation to a O(1) formula? If not, then how do I determine that the recurrence relation does not have an implicit formula? If yes, then is there any rule of thumb for converting?











Click
Hahaha, it links back to the this page!
Ok, check this.
This is so dumb, why is it so hard for you to check your own lmgtfy before posting? It doesn't provide any clear immediate answer and this page is among google search results.
We got him
You may want to look up methods of solving recurrences in some book or on the net. Without going into the details, I'll just tell you that the fibonacci series indeed has a formula involving the golden ratio, it's called Binet's Formula. You may want to look at this page to get started.
Binet's formula is an approximation formula. It does not give precise values for large n
No Binet's formula is exact. In programming it's not, as doubles aren't arbitrary precision. But the formula itself is exact.
It can be done exact in modular arithmetics for modulos that have a square root for 5. Such as in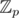 where p = 109 + 9.
where p = 109 + 9.
Yeah... that problem (DZY Loves Fibonacci) was kinda lame imo. Finding quadratic reciprocity isn't that easy of a task itself. There were a lot better solutions that didn't rely on that.
I'd say it's cool, but not a good idea for a problem in a rated contest. It requires much more than the problem itself, such as an already-implemented Tonelli-Shanks template on your personal computer :D
If recurrence is generated by linear composition of previous values, it can be rewritten in matrix form, and then matrix power has closed form granted by Jordan form. But it, of course, involves n-th powers of eigenvalues.
If you have f(n)=af(n-1)+bf(n-2)+cf(n-3)+df(n-4)+ef(n-5)+ff(n-6), then to solve for f(n) you need to find roots of f+ex+dx^2+cx^3+bx^4+ax^5=x^6. Then f(n) will be linear combination of these roots to the nth power. But it is really hard to solve nth degree polynomial.
This is simple consequence of eigenvalues of matrix
Yes, but it is not a closed form formula.
It is.
Please, provide exact definition of "simple recurrence relation". We can't speak about generic solutions before we make our terms consistent.
For linear recurrent relations solution is well known.
Binet's formula Fn=(((1+√5)/2)^n − ((1−√5)/2)^n)/√5
I don't know many things about it, but in that case there wouldn't be any DP!!!
You could just solve it O(1), am I wrong?? Or maybe that's because it's really hard to get the O(1) formula...
There exist two types of recurrences: ones that have closed forms and ones that don't.
For the first type of recurrences, with closed forms, still, one may not be able to calculate the nth term in O(1). Just like Fibonnaci sequence, one need to calculate it in at least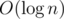 time.
time.
For the second type, there's no such formula exist, not to mention the complexity.