Someone Please Explain D,E solution(English)?It's in Japanese
→ Pay attention
Before contest
Codeforces Round 940 (Div. 2) and CodeCraft-23
23:07:54
Register now »
Codeforces Round 940 (Div. 2) and CodeCraft-23
23:07:54
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3648 |
| 2 | Benq | 3580 |
| 3 | orzdevinwang | 3570 |
| 4 | cnnfls_csy | 3569 |
| 5 | Geothermal | 3568 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3530 |
| 8 | Radewoosh | 3520 |
| 9 | Um_nik | 3481 |
| 10 | jiangly | 3467 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 163 |
| 4 | TheScrasse | 159 |
| 4 | nor | 159 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 150 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/20/2024 18:27:08 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










My solution for D: It can be observed that the whole game consists of two phases: In the first phase Takahashi will take the greatest numbers, which Aoki will take some numbers around x. In the second phase the two will alternately take the greatest number. One should binary search on the position such where the transition between two phases happen. To check it one may need another binary search to count the numbers taken. After that the sum can be computed in O(1) if precalculated the partial sums and partial sum on even indices. The solution takes time.
time.
Can u explain the two phase in above test case.Thanks
5 5
3 5 7 11 13
1
4
9
10
13
I'll explain the third query. I'll use T for Takahashi and A for Aoki. First T takes 13, A takes 7, and then T takes 11. Then A was supposed to take 11, but it is already taken by A. This is where the transition happens: the two players' territory(I don't know if this is clear enough) intersects. From now on, A and T will alternately take the greatest number remaining, which is: A takes 5 and T takes 3.
I had a similar idea: a suffix of A will be taken by Takashi, some part (same length or one less) before that by Aoki and the remaining prefix alternatingly. Then I processed the queries sorted decreasingly and kept pointers to the borders, so it's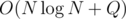 .
.
edit: It's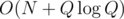
Oh yes, this can be done more efficiently if processed offline. But I think that's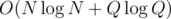 due to the sorting process :D
due to the sorting process :D
Yeah, I added the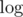 in the wrong place :D
in the wrong place :D
How to find the position of transition?
In fact, I binary searched on the suffix that was taken by Takahashi. which requires the length of the region of Takahashi to be at most one more than the length of the region of Aoki. This may be hard to explain, you may refer to my code. Code
why l=pos-1 in ur code?
and ll numl=mid-(lower_bound(a,a+n+1,2*x-a[mid])-a) what it does?
The first one is because I choose r as the final answer, and pos is an valid answer. The second one implies the amount of numbers in Aoki's region.
My solution for E: Let dpv, j, 0 denote the minimum sum of Ai in the connected component of v if we cut j edges in the subtree of v, and the connected component of v only consists of batteries. And dpv, j, 1 denote pretty much the same thing, but allows the connected component of v consists of computers. The DP should be calculated in an ordinary manner, which may seem to have a complexity of O(N3), but is actually O(N2). There are many proofs given on this kind of problems, e.g., Barricades in Algorithmic Engagements 2007, which can be found in the book looking for a challenge