Hi all,
The second contest of the 2018-2019 USACO season will be running from January 18th to January 21st. Good luck to everyone! Please wait until the contest is over for everyone before discussing problems here.
EDIT: As a reminder, do not post any spoilers until the contest is over, which will be at 4 AM UTC-12 on January 22nd. If you have any issues with the problem statements, please consult the rules on how to contact the contest administrators. The administrators do not monitor social media.











Does anyone know how to solve Gold #2?
bro
Totally The Real Solution
The USACO Discord sends its love!
This comment is almost as geniosity as summitwei.
How is summit such a god and frodakcin such a prodakcin
EDIT EDIT: Okay it's actually over now
I ACed gold P1 and gold P2, but unfortunately didn't have time to implement and debug P3 in one hour. It didn't seem very hard at all but my idea could have been wrong.
In some cases this has been enough for plat but I haven't got my hopes up.
Contestants cannot start anymore, but some may still be working. Please wait for discussion.
It is now 4 AM UTC-12 on January 22nd.
Thanks to pacu for being a stellar problem writer (all three in Platinum)!
I can't wait for results to be released :D
How to solve platinum P3?
Since the contest is over now, does anyone know how to solve Gold #1?
Write out a formula and use modular exponentation for an solution (mine ACed)
solution (mine ACed)
Solutions to plat problems:
Convert each 'G' to +1 and each 'H' to -1. Now the problem asks to split the array into segments such that we have minimal number of segments with positive sum and the length of each segment is ≤ K.
We will solve this with DP. The state is dp[position] = answer for the prefix [1;position]. It can be easily solved in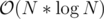 by doing a sliding window with a segment tree.
by doing a sliding window with a segment tree.
Code
Main observation is that we need to find the number of pairs of cycles that are edge-intersecting. Now if we root the tree and for each cycle find the LCA of its two vertices, then for each pair of intersecting cycles the LCA of one of them w will be above (or they will have the same LCA). We will consider the case of same LCA separately. The other case can be done with a DFS + segment tree/Fenwick on DFS order. Look at the code for details. The complexity is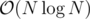 .
.
Code
My solution's time complexity is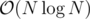 , but it can be easily improved to
, but it can be easily improved to 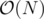 .
.
Lets solve the problem for the interval (X, Y) of the K-minimums. Now find the minimum value in it. We will denote it as a[P]. Also we will extend [P;P] to the left and right while the value of a[P - 1] is the same as the value of a[P]. Now we have an interval [L;R] such that everything in it is equal to the minimum value.
Obviously if L > X, a[L] < a[L - 1] and if R < Y, a[R] < a[R + 1]. From here we can notice that if L > X, Value[L + K - 1] should be exactly equal to MIN and all values in the interval [L - 1, L + K - 2] should be > MIN. This means that the values in [X;L + K - 2] and [L + K - 1;Y] are independent.
Similarly, but for R, we have that Value[R] should be exactly MIN and everything in the interval [R + 1, R + K] will be > MIN. And we get that interval [R + 1, Y] is independent.
So from the above two we can do the following D&C algorithm:
1) Define solve(X, Y) being the answer for [X;Y]. The answer to the problem is solve(1, N - K + 1).
2) Find L and R as described above. This can be done in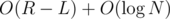 time with segment tree.
time with segment tree.
3) If X < L multiply the return value of the current solve() by solve(X, L - 1).
4) If R < Y multiply the return value of the current solve() by solve(R + 1, Y).
5) Now multiply the return value of the current solve() by the number of ways to fix the values corresponding to the K-minimums in the interval [L;R]. This can be done in O(R - L) with a simple dp.
6) Return the value.
The complexity will be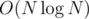 because of the segment tree. To reduce it to linear time, we can just find the intervals with equal values with one linear pass.
because of the segment tree. To reduce it to linear time, we can just find the intervals with equal values with one linear pass.
Code
You can solve redistricting in O(N) using DP + deque.
Would you like to explain for exercise, in the solution, " If the two non-standard trails we are considering have edge-disjoint paths, then it is not possible to create a simple cycle with them. However, if their paths do overlap, then we can create exactly one simple cycle." why we can only create one simple cycle? wouldnt the sample case be the counterexample?
Was #2 Gold supposed to be solved with policy based data structures?
It can be solved with BIT too.
Can you elaborate a little bit on how to solve? I tried using binary search and naive shuffling to no avail.
take the longest descending subarray from the back (i.e a[x] < a[x+1] < .. < a[n]) now insert the elements a[1] to a[x-1] at the right positions in this subarray using PBDS/BIT etc
How does using a BIT or PBDS make the runtime any different from using binary search and inserting the elements at their respective spots? Sorry if this is a dumb question lol
Could it be due to the complexity of inserting in the vector which you are binary searching in? I think that's linear, while point update in a BIT is logarithmic. I wonder if using a set would allow binary search to pass...
(I didn't solve the problem either, by the way)
It doesn't. One of my friends solved it using binary search and the insert function.
Could you explain how this TLE's then? I'm absolutely stumped.
Code: https://pastebin.com/kkZVd5u7
Yeah, like I said, it's probably because you are using ArrayList (which has linear complexity for insertion) and not a TreeSet.
Can someone tell me if I was at least on the right track for Gold #3, and if so, where I went wrong?
Code: https://pastebin.com/2NEWWT9P
Using Djikstras to store the parent for every node then backtracking is the correct approach. I believe where you went wrong is when you tried to make sure every cow moved on the lexicographically shortest path. You seem to check for that in the compareTo of the Pair (which are your Edges), but you actually should be checking the vertex id's inside the for loop at line 46. You need to compare to parent of the node at the other end of the edge and current node. The if statement that you are missing is
Gold P1 was mine. Solution sketch:
Start by computing the number of possible lines ending in each rhyme class. This can be done using a fairly standard coin DP. Essentially, we have N+K states--one for each of the N possible incomplete line states and for the K possible rhyme classes for completed lines. The N words are our transitions, so in total this has efficiency O(N(N+K)). Note that doing a separate DP for every single rhyme class will be too slow, as this has runtime efficiency O(N^2K), so the key observation is that we can reuse all of potential incomplete lines no matter which rhyme class we're ending with.
Now, for each number of lines X such that some letter appears X times in the rhyme scheme, we want to know how many ways there are to create a set of X rhyming lines. This is fairly easy as well--if dp(i) is the number of lines ending in rhyme scheme i, the number of sets of rhyming lines is the sum of dp(i)^X over all i, since there are dp(i) ways to pick the first line, dp(i) ways to choose the second, and so on. Note that because X can be up to 10^5 and we could have up to N rhyme classes, we'll need to use an efficient exponentiation algorithm. Here's some pseudocode:
This algorithm runs in O(log X). (You have to be careful while implementing to frequently take the value mod 1,000,000,007 to prevent overflow.)
Finally, to compute the answer, we multiply the above values for each letter appearing in the rhyme scheme together.
Results and editorials are up at http://usaco.org/index.php?page=jan19results!