After applying Gaussian algorithm on a array how could I restore those numbers of which XOR is maximum?
Let a[3] = {11, 5, 9} If I apply Gaussian algorithm we will find maximum xor is 14.And used numbers are 11, 5.How to restore this 11, 5?
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
After applying Gaussian algorithm on a array how could I restore those numbers of which XOR is maximum?
Let a[3] = {11, 5, 9} If I apply Gaussian algorithm we will find maximum xor is 14.And used numbers are 11, 5.How to restore this 11, 5?
| Name |
|---|



if you have additional time (where c is the max value) it is easy to restore. Here is a slow implementation, which can be improved to
time (where c is the max value) it is easy to restore. Here is a slow implementation, which can be improved to 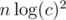 if you replace the bitset and just store by wich indices the value is composed (there are always atmost
if you replace the bitset and just store by wich indices the value is composed (there are always atmost  bits set).
bits set).
Thanks man. I got. :)
I did a python 2 implementation to show one way of doing it, in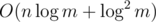 , where m is the number of linear independent binary vectors in A. Note that
, where m is the number of linear independent binary vectors in A. Note that  so it runs really quick, also note that nothing in my implementation is python specific I just really like how pseudo code like python is. The essential stuff lies in the two functions, the rest just shows how to use the functions.
so it runs really quick, also note that nothing in my implementation is python specific I just really like how pseudo code like python is. The essential stuff lies in the two functions, the rest just shows how to use the functions.
The output is
I didn't get anything. I have a little knowledge of python. But thanks.You tried to help me.