Hello i am just trying to solve this series 1/12 + 11/12^2 + (11*11)/12^3+...... first i need to tell you what my approach to solve which prove me wrong what i got is this is a gp so sum of finite term of gp is :Sn=a(1-r^n)/(1-r) for this series we know 0<r<1 as r comes out to be r=11/12 so consideration of this series — values come out to be a=1/12 , r=11/12 Sn=((1/12)(1-(11/12)^n)) / (1-11/12)
to compute 11^n and 12^n it take so much time with brute force so i optimize and take time log(n) now after some solving what i get is Sn=(12^n-11^n)/12^n. now n could be very large so 12^n or 11^n could be very large and we out of bounds so we need to modulo him to to get 12^n and 11^n with in the range .
lets take an example where i take n=36 my fastpower function which take less time
mod=1e9+7;
ll power(ll x,ll y){
ll te=1; if(y==0)return 1; te=power(x,y/2); if(y%2==0)return (te*te)%mod; return (te*te*x)%mod;
} int main(){
long long a=(power(12,36) - power(11,36)) / power(12,36);
} i need to find a as this is sum of finite series bu it comes out to be negative....
when i solve this i get 12^36 <11^36 and gives me finite sum of this series negative ans
Sn=(12^n-11^n)/12^n as 12^n<11^n Sn =-ve i have got i really didnt know how to solve after that i just need this series in p/q form and i need to take multiplicaive inverse of q which is later thing but first i need to solve this series and get the p/q form
someone help me out..... thankyou....










I believe "(te*te*x)%mod" might overflow before you take the modulo. I also believe that you need to use modular inverse to calculate this.
The reason for 12^36 < 11^36 is the modulo. However, this isn't a problem. For example: 2*3 < 2*2 (mod 5), even though 6 > 4.
Please, stop down voting this comment or explain your position. TS is trying to make modular division in very strange way. Kallaseldor suggest modular inverse, because modular division is defined when modular inverse of the divisor exists. If you think its wrong — post why.
thankyou for look into it but still i am not get it.Suppose i take n=36 as i described above now how you compute this value 1-(11^n/12^n) and u need to take the multiplicative inverse of denominator with 1e9+7.
(12^n-11^n)/12^n = ?? i am stuck at this place if you explain this then surely i will got that. thankyou..
Which answer do you expect for n = 1?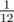 or 83333334? What is the maximum value for n?
or 83333334? What is the maximum value for n?
for n=1 ans=83333334 as we take multiplicative inverse of den with 1e9+7. so i want ans for value n= >=36.
Oh, ok. Here is C code for calculating the answers for n = 1... 36. Hope it helps.
Sorry I understand nothing. "i am just trying to solve this series"... What does it mean? Yes, you are right that But what's next?
But what's next?
Do you want to represent S(n) as a fraction for some value n? Then you need long arithmetic, because 11n and 12n become very large for large n. Or do you like to find the value S(n) when n → ∞? It's 1.
for some value n? Then you need long arithmetic, because 11n and 12n become very large for large n. Or do you like to find the value S(n) when n → ∞? It's 1.
How can we apply here the modular arithmetic? As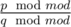 ? It's nonsense. Sorry, I do not understand.
? It's nonsense. Sorry, I do not understand.
1 / X = X ^ -1 = X ^ (M — 2) (mod M) for any prime M.
Therefore, P / Q = P * Q ^ -1 = P * Q ^ (M — 2) (mod M).