Hi everyone. Today I encountered a data structures problem, which is a slight swist on standart segment tree problem.
You are given an array A of size N. N ≤ 10^5, A[i] ≤ 10^6, You need to process 3 types of queries
Print the sum of all integers ai where L ≤ i ≤ R.
Add x to each integer ai where L ≤ i ≤ R.
For each integer A[i] where L ≤ i ≤ R, replace it with floor(sqrt(A[i])). Where sqrt(a) is the square root of a, and floor(b) is the integer value of b after removing everything on the right of the decimal point.
There can be Q≤20000 queries.
If we didn't have type 3 query, then we are left with standard lazy segment tree problem.
How to handle 3rd type queries?











I think the problem you are talking about was in ACPC 2016, this problem to be exact.
I didn't solve it, however, I was told by one of the judges during the contest that it can be solved by holding the maximum and minimum in the range of the segment tree and using lazy propagation in the form of vectors and since any range will become equal after not that much operations when the maximum becomes equal to minimum it's easy to note that lazy propagation becomes easier to do in O(1).
I don't know exact time complexity of this solution. Firstly we store maximum and minimum in our segment tree. We will have three options.
Can you please explain the 2nd option?
How can we obtain it(the new version of the segment, after applying sqrt) by adding (sqrt(minimum) — minimum) to this segment elements?
It can be done using segment tree with lazy propagation which supports adding and assigning. We can support it just only using one segment tree.
I mean the following:
Suppose the segment is [11,5,7,10,6]
After applying sqrt we should get [3,2,2,3,2] right?
But if we do it your way i.e. by adding (sqrt(minimum) — minimum) to this segment — we get
sqrt(minimum) — minimum = sqrt(5) — 5 = -3
So we add -3 to the range and get [8,2,4,7,3]. Which is different than [3,2,2,3,2].
We will have an array [11, 5, 7, 10, 6]. No condition meets. (11 — 5 != 1)
So, we will divide it into two [11, 5], [7, 10, 6]. Also no condition meets.
[11], [5], [7], [10, 6]
[11], [5], [7], [10], [6] => [3,2,2,3,2]
Thanks Zharaskhan got your point. Can you provide intuition why this works fast? In this query example we saw that it is linear.
I think the idea is if max - min ≥ 2, then it will decrease proportional to sqrt(N). So 2nd type queries won't ruin everything because the difference will still decrease quickly.
But it's possible that max - min = 1 and still will be after taking square roots for each element. For example [3, 4] to [1, 2]. So if we're able to do such updates without solving recursively, we can solve the problem.
If we know min = max - 1 then we can, for example, use counts for min or max and update the interval without the need of recursive.
That's nice solution.
What is the complexity of this solution?
Thank you!
Would the solution be considerably worse if we solve option 2 recursively?
EDIT: Nevermind, I finally understood the corner case.
For query type 3:
when we get the range modification entry, we can modify each element in the range one by one, and hence perform (R — L + 1) single element update queries. This approach would be to slow, as it makes the complexity of range update query to O ((R — L + 1) lg N). But many of these single element update queries can be ignored, and the number of actual performed queries is much lower.
Note that, if the value of an element A[x] is 1, then update query on A[x] does not have any effect on the segment tree.Let call such queries as degenerate queries, and We can discard them. Now think A[x]>1, then how many update operation is required on that position to make the A[x] is 1. It will require less than lg(A[x]) operation approximately.So,every node of segment tree gets updated at most lg(10^6) time . However, now the problem is how to find the non-degenerate single element update queries for the range [L, R]. For this purpose, we maintain another information in the segment tree node, which is the number of elements in the range which are larger than one.
Similar problem You can see editorial for better explanation .
What if we have lots of 2nd type queries, such that A[i] is never becoming 1? This way the complexity may be upto O(n) for each query.
My guess is that you can do it with a small modification to the lazy segment tree. For each node in the tree keep track of whether or not its corresponding interval is constant. Then when you get a query of type 3, you can lazily take care of it if the interval is constant, otherwise let the children nodes handle the query.
The reason why I think that this works is that floor(sqrt( )) is really destructive. Suppose you start out with A[i] ≥ 1, then after you apply query 3 enough times to it, the new value is independent of its original value. You would have gotten the exact same result had A[i] = 1 in the beginning. This in turn makes intervals become constant, which allows queries of type 3 to be taken care of lazily.
It seems like a good idea. Btw do you have an intuitive reasoning why should the invervals become constant quickly? We have 2nd type queries which may ruin everything.
Also do you have an estimate of time complexity? In the worst case it may be linear per query, this can happen if all internal(non-leaf) segments aren't constant.
(Note there is a small error in my approach, so just use Zharaskhan approach, still here is the analysis for the running time)
Assuming that x > y ≥ 1, from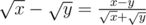 .
.
one can show that
This describes how quickly the difference between two values x, y decreases when you apply a floor(sqrt( )) on the pair. It will pretty much decrease with a factor of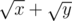 , so it decreases very quickly.
, so it decreases very quickly.
I did some calculations given the second inequality and from that I concluded that it takes at most 5 iterations for the difference to become ≤ 1.
Finally, about the running time. For each node in the tree you need to apply type3 queries 5 times to reach max - min ≤ 1. Also whenever you do a type2 or type3 query you will update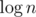 nodes, which after 5 type3 updates will go back to have max - min ≤ 1. So from this I conclude that the running time should be something like
nodes, which after 5 type3 updates will go back to have max - min ≤ 1. So from this I conclude that the running time should be something like 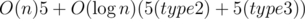 .
.
If you have 3s and 4s and alternate sqrts and +=2 I think you'll never get constant and you will have linear sqrt updates
Thanks for pointing that out, that is a problem.
I think it is possible to fix it by keeping track of whether or not the interval only contains at most two different values (and keep a count for both). But if you do that, then you might as well just do the min/max approach that Zharaskhan mentioned.
Can I submit this problem somewhere? It seems the ICPC Live Archive doesn't have any input (my assertion
assert(ntest > 0)failed).I can't think of an Segment Tree solution so here goes my shitty sqrt one:
Let's process one block of T queries at a time (we will choose T later). We divide the N numbers into intervals, with starting points being L[1], L[2], ..., L[T], R[1] + 1, R[2] + 1, ..., R[T] + 1. This way we have at most 2T intervals, and each query cover some intervals completely. For each interval, we store those values: min, max, sum, offset, count of elements equal to min/max.
For the "add X" queries, we simply increase the offset of the affected intervals by X.
For the "take sqrt" queries, we notice that after at most 6 "sqrt" queries, max[b] - min[b] ≤ 1 will hold, because the value of A[i] won't exceed 226 and the "add" queries won't change max[b] - min[b]. Thus, if max[b] - min[b] > 1 holds at the moment, we just recompute all elements of block b, knowing we won't do that more than 6 times per block, and update the min, max, and sum accordingly. Otherwise, we can set
min[b] = sqrt(min[b] + offset[b]), max[b] = sqrt(max[b] + offset[b]);and ignore valuesumbecause it can be deduced (see below).For the "compute sum" queries, we compute the sum of each block. For block b:
If min[b] = max[b] then sum[b] = min[b] * cntmin[b] + offset[b] * length[b].
If min[b] + 1 = max[b] then sum[b] = min[b] * cntmin[b] + max[b] * cntmax[b] + offset[b] * length[b].
Otherwise, we just return sum[b].
After processing T queries, we need to retrieve the new array A (I did that in O(N * log(N)), not sure if it can be done faster).
The time complexity is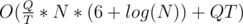 , where 6 = log2(log2(maxA)).
, where 6 = log2(log2(maxA)).
Code with T = 500 that produces the same answer as my brute force solution
Probably you can download here: http://acmacpc.org/archive/y2017/
I tried but it says "404 page not found"...
I think you can submit the problem from here :
https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=804&page=show_problem&problem=6491
Already did but my assertion
assert(ntest > 0);fails, which likely means the judge has no input.