Hello $$$\mathfrak{Code}\color{blue}{\mathfrak{Forces}}$$$,
This blog assumes that you are already familiar with the basic concepts of Graph Theory.
First of all I'd like to thank my coach fegla who taught me those tricks and I'll try to share some of them with you. I think that there is no tutorial for this graph representation (at least no English tutorial, I've seen some Chinese coders using this representation). So, here we go!
I'd like to introduce this uncommon graph representation (I'm not sure if it has a proper name or not, but we used to call it adjacency edge list).
Let's say we have this directed graph: note that the numbers on edges are just the order of adding edges:
0 1
0 3
1 2
2 3
0 2
2 4
3 4
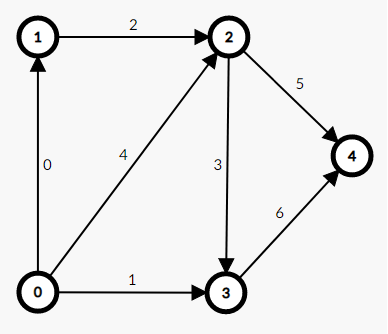
We will represent this graph using only two arrays/vectors:
int head[MAX_NODES]; the size of this array will be the maximum number of nodes, and the value for each node will represent the index of the latest added outgoing edge in the edges array.
edgeData edges[MAX_EDGES]; the size of this array will be the maximum number of edges, it contains all the needed data from the edge. and the edgeData must contain nxt which will point to the index of the next edge.
Let's see all the outgoing edges from node $$$0$$$, the indices of the edges in order are $$$[0, 1, 4]$$$. initially head[0] = -1 which means that there is no outgoing edges from node $$$0$$$.
Let's add the edge with index $$$0$$$ 0 1 we will update edges[0].to = 1, edges[0].nxt = head[0], which means that edges[0].nxt = -1. after that update the head to the index of this edge head[0] = 0.
Let's add the edge with index $$$1$$$ 0 3 we will update edges[1].to = 3, edges[1].nxt = head[0], which means that edges[1].nxt = 0. after that update the head to the index of this edge head[0] = 1.
Let's add the edge with index $$$4$$$ 0 2 we will update edges[4].to = 2, edges[4].nxt = head[0], which means that edges[0].nxt = 1. after that update the head to the index of this edge head[0] = 4.
Now, Can you guess how to traverse the next neighbor nodes from node $$$0$$$?
So, it's more like we push_front the edges, the new edge will point to the last edge added which is head[node], then we can update head[node] to point to the new added edge.
Next tables show the updates after adding the edges mentioned before in order.
| Updates for head array | Updates for nxt in edges array | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
..
$$$ $$$
Undirected graph trick
It's obvious how to create undirected graph (just add two opposite edges).
The trick is when we add the first directed edge, we must add the opposite one directly after it, so their indices are next to each other.
So the first edge will have two directed edges with indices $$${0, 1}$$$, and the second edge with indices $$${2, 3}$$$, and so on.
This trick is very useful when we have an edge and we want to get the opposite edge in min cost max flow algorithms.
Can you guess how to do this quickly in $$$\mathcal{O}(1)$$$?
Why this is useful?
If you know the maximum number of edges from the start, then you can allocate the exact needed memory to the arrays on the stack or data segment, this is useful when you work on embedded systems where you cannot allocate memory on the heap.
Sometimes we need to visit edges in a graph, so I think this representation is more convenient, because each edge has its own index.
Maintainable, sometimes when you need to add extra information to the edges, all you need to do is add the info to edgeData struct, and you will not change a lot in the old code.
That's it, Thanks for reading and I hope it was useful. Any suggestions or improvements are welcome.











Really good post on this presentation. Well yes, I also did not see any tutorial or post about this presentation online or anywhere. Though I did find this post some years ago about implementing multiple stacks with efficiency memory. The idea in the post is similar to yours. I think it is nice to point this out because it is more general data structure and also have another application beside representing a graph.
Thanks for sharing this, it's my first time seeing this, and yeah it's the same idea, that's really cool :)
That's very cool, thank you :)
I wonder where this could be useful. Aside of allocating the memory beforehand, I feel like this actual cause massive overhead for any graph algorithm, as the jumps introduced when traversing all edges might cause a lot of cache misses. Maybe if the graph change a-lot, we might gain something from the pre-allocation.
I know of another data structure which is used in Galios and other graphs library which is similar in a sense to this, but is more efficient cache-wise.
The edges should be given beforehand, so this time it's for static graphs. The "Edges" array hold all the edges, order such that first there's all the edges from node 0, then 1, and so on. The "Head" array hold index of the first edge index of the node. So traversing the edges become going over an array from one index to the other, and because all edges are on a single array continues in memory, you get a very good cache-miss overhead.
I agree, but comparing to the normal adjacency list, I think this method is more efficient, I've tried this in some problems on different online judges specially problems with flows, and it was better than the normal adjacency list. I guess I've to do some comparisons on different graph algorithms and see the results.
Very lovely explanation! I was happy to finally see a written explanation of this method after learning it from fegla! There is an interesting thing about this method, with a very tiny edit, we can implement a sort-of visited flag over the edges we traverse in a dfs, if we set 'e' to be a reference variable and update it before we recurse, we guarantee that an edge is not visited twice (because it is "removed" from the adj list). Because e is a reference, each iteration overrides the current edge with the next edge, this eventually leads to all edges being removed, hence "visited". This can be a fun way to implement an Euler path.
Unfortunately, this only works for the forward edge, in an undirected graph, this does not automatically remove the back edge. We can fix this by including a visited array over the edges as normal. While this does not make the trick as elegant, it is more efficient (because under no circumstances an edge is ever visited more than twice)
How is this uncommon? It's on the Wikipedia page of Adjacency list , which cites Introduction to Algorithms for the idea.
I'm not sure if you read the blog carefully, This is different from the normal adjacency list. The method I mentioned here has two arrays (head, edges), on the other hand, the adjacency list has maybe vector<vector> or whatever representation.
I'm not sure if you read the Wikipedia page carefully, so I copy it here for you.
Cormen et al. suggest an implementation in which the vertices are represented by index numbers.[2] Their representation uses an array indexed by vertex number, in which the array cell for each vertex points to a singly linked list of the neighboring vertices of that vertex. In this representation, the nodes of the singly linked list may be interpreted as edge objects; however, they do not store the full information about each edge (they only store one of the two endpoints of the edge) and in undirected graphs there will be two different linked list nodes for each edge (one within the lists for each of the two endpoints of the edge).
Well, I've read this paragraph multiple times, and what I understood is it describes the normal adjacency list, correct me If I'm missing something!
It means that each vertex has its own linked list, but this is different from what I described in the blog.
What is described here is: each edge has its own index in array, and each edge is pointing to next edge, and we have another array where each vertex is pointing to the index of last added edge.
Can you show me any equivalent sentences in the article you mentioned? as I cannot see how it's the same thing?
It's just the matter of how linked list is implemented.
Your method is just the normal adjacency list described on Wikipedia with linked list implemented with "pre-allocated array and index".
Most of the properties remain even if you implement it with "dynamically allocated memory and pointer". Each edge has its own address in memory, and each edge is pointing to next edge, and we have another array where each vertex is pointing to the address of last added edge.
Does anybody have problems that can be solved efficiently using this representation and is much better than other representations?