[This article is also available in English]

Привет, CodeForces.

Я думаю, что матроиды — это прекрасные и очень мощные структуры, однако, не настолько хорошо известные в спортивном программировании.

Я познакомился с матроидами на Зимних Петрозаводских Сборах 2019. Там была задача, которая очевидно не решалась обычными способами, известными мне тогда. Разбор этой задачи состоял буквально из трех слов “just matroid intersection”. Тогда мне потребовалось больше двух дней дорешивания чтоб найти всю необходимую информацию и детали и написать решение, которое получает Accepted. И намного больше времени мне потребовалось чтобы понять почему это действительно работает и как именно это работает. (Я до сих пор сомневаюсь в некоторых деталях.)

Конечно, совершенно не трудно нагуглить все необходимые определения и статьи, связанные с этой темой, но мне кажется, что все они больше сконцентрированы на математической теории, строгих и коротких доказательствах какими-то не особо очевидными путями и рассматривают только ключевые положения всей теории пропуская множество логических шагов, промежуточных результатов и примеров. Я встретил такое загруженное формулами доказательство в одной из статей:

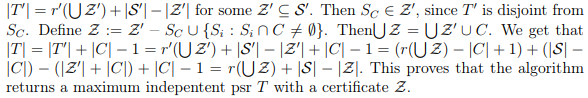
Это было даже не близко к тому, чтобы быть понятным для меня тогда. (Возможно я просто недостаточно математик для этого, пока что.) Но все же, я уверен что существует способ сделать его более понятным, очевидным и детализированным.

Я уверен, в спортивном программировании есть много людей, которые бы тоже хотели познакомиться с матроидами. И поэтому я решил рассмотреть эту тему с самого начала фокусируясь больше на объяснениях, логических шагах и предоставлении большего числа примеров. Это и есть цель этой статьи и вам не обязательно знать что-либо о матроидах для прочтения. .

Необходимые знания. Не требуется хорошо знать все перечисленное тут, но хорошо быть знакомым с частью этого списка, для более быстрого и лучшего понимания:

1. Основы теории множеств, операции над множествами
2. Остовные деревья в графах
3. Паросочетания в двудольных графах
4. Линейная независимость в векторных пространствах
5. Ранк и базис множества векторов
6. Метод Гаусса
7. Алгоритм Краскала для поиска минимального остовного дерева
8. Алгоритм Куна для поиска максимального паросочетания в двудольном графе
9. Удовольствие от дискретной математики

Вся информация в этой статье — это мое понимание этой темы, которое основывается на изучении других статей из интернета. Как известно, доказательство с помощью прохождения тестов доказательством не является. Поэтому если вы нашли что-то нелогичное или неверное, это значит, что я совершил ошибку или что-то понял не так, пожалуйста напишите об этом.

Что такое матроид?

Матроид — это структура, которая обобщает понятие линейной независимости в векторных пространствах.

Вот формальные определение. Матроид — это пара $$$\left\langle X, I \right\rangle$$$ где $$$X$$$ называется носителем матроида (ground set), а $$$I$$$ — это множество всех независимых подмножеств $$$X$$$. Другими словами матроид $$$\left\langle X, I \right\rangle$$$ дает классификацию каждому подмножеству $$$X$$$: или оно независимо, или зависимо (включено в $$$I$$$ или не включено в $$$I$$$).

Конечно, мы не рассматриваем произвольные классификации. Эти $$$3$$$ свойства должны выполняться для каждого матроида:

1. Пустое множество независимо.
2. Любое подмножество независимого множества также независимо.
3. Если независимое множество $$$A$$$ имеет меньший размер, чем независимое множество $$$B$$$, существует как минимум один элемент из $$$B$$$, который может быть добавлен в $$$A$$$ без потери независимости.

Это аксиоматические свойства матроида. Для доказательства, что мы имеем дело с матроидом, нам в общем случае нужно доказать эти три свойства.

Для примера, явное представление матроида на носителе $$$\{x, y, z\}$$$, который считает $$$\{y, z\}$$$ и $$$\{x, y, z\}$$$ зависимыми, они отмечены красным. Остальные множества независимы и отмечены зеленым.

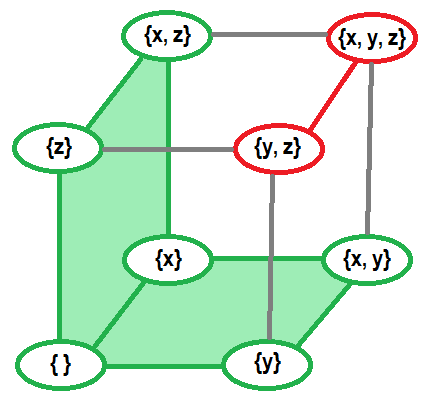
Из этого определения мы можем вывести другие важные понятия (примеры всех этих понятий будут приведены ниже, вместе с примерами матроидов):

Базисы. (bases) Каждое независимое множество максимального размера считается базисом своего матроида. Другими словами, не существует элемента, который может быть добавлен к базису без потери независимости. Все базисы имеют одинаковый размер (иначе мы могли бы добавить что-нибудь из меньшего базиса в больший по третьему аксиоматическому свойству). Прямо из предыдущего, никакой базис не является подмножеством другого базиса. Любое независимое множество — это подмножество какого-то базиса (мы можем добавлять элементы в независимое множество по третьему свойству до тех пор, пока не достигнем какого-нибудь базиса), так достаточно только иметь информацию о всех базисах матроида для того, чтобы полностью его описать.

Циклы. (circuits) Зависимое множество называется циклом в случае, если все его подмножества (не включая все множество) независимы. Другими словами, цикл — это зависимое множество, из которого нельзя ничего исключить сохранив при этом зависимость. Никакой цикл не является подмножеством другого цикла (иначе мы могли бы исключить из большего цикла что-нибудь получив при этом зависимое множество в виде другого цикла). Любое зависимое множество содержит в себе хотя бы один цикл как подмножество. Аналогично базисам, достаточно иметь информацию о всех циклах матроида, для того, чтоб полностью его описать.

Еще одно важное свойство циклов матроида: из объединения двух циклов можно исключить любой элемент и в нем все равно будет содержаться какой-нибудь цикл. Для определенных видов матроидов можно сформулировать более строгое свойство: симметрическая разность двух циклов всегда содержит цикл. Симметрическая разность двух множеств содержит все элементы, которые включены только в одно из этих множеств (формально, $$$A \Delta B = (A \setminus B) \cup (B \setminus A)$$$). Например, это свойство относится к пространствам циклов в графах.

Ранги. Ранговые функции. (rank) Ранг матроида — это размер его базиса. Но ведь можно так и говорить об этом — размер базиса матроида, зачем для этого особое определение? Да, это не очень гибкое определение. Чтобы придать ему больше гибкости можно определить ранговую функцию $$$r(S)$$$, которая будет говорить размер максимального независимого подмножества $$$S$$$, где $$$S$$$ — это подмножество носителя $$$X$$$. Ранг подмножества в матроиде — это значение ранговой функции на этом подмножестве. Эта информация о подмножествах может быть очень полезной во многих ситуациях. Некоторые свойства ранговых функций:

1. Ранг подмножества не может быть больше, чем размер этого подмножества.
2. Ранг независимого множества — это его размер.
3. Ранг всего носителя матроида равен рангу матроида. Ранг пустого множества равен $$$0$$$.
4. Ранг подмножества $$$S$$$ не может быть больше, чем ранг всего множества $$$S$$$.
5. Добавление $$$1$$$ элемента к множеству может только увеличить его ранг на $$$1$$$ или оставить ранг неизменным. (формально, для множества $$$S$$$ и элемента $$$x \notin S$$$ мы имеем $$$r(S) \leq r(S \cup \{x\}) \leq r(S)+1$$$)
6. Ранговая функция матроида полумодулярна (submodular). Если у нас есть два множества $$$A$$$ и $$$B$$$, перемещение всех элементов, которые есть в $$$B$$$, но не в $$$A$$$, из $$$B$$$ в $$$A$$$ не может увеличить сумму рангов этих множеств. Формально, $$$r(A) + r(B) \geq r(A \cup B) + r(A \cap B)$$$. В общем элемент не будет оказывать больший вклад в ранг, если его переместить во множество с дополнительными элементам. Это может стать более понятным, если явно разделить $$$A$$$ и $$$B$$$ на $$$A’ = A \setminus B$$$, $$$C’ = A \cap B$$$ и $$$B’ = B \setminus A$$$ и записать все это в форме $$$r(A’ \cup C’) + r(B’ \cup C’) \geq r(A’ \cup B’ \cup C’) + r(C’)$$$. Пример изображен на картинках ниже:

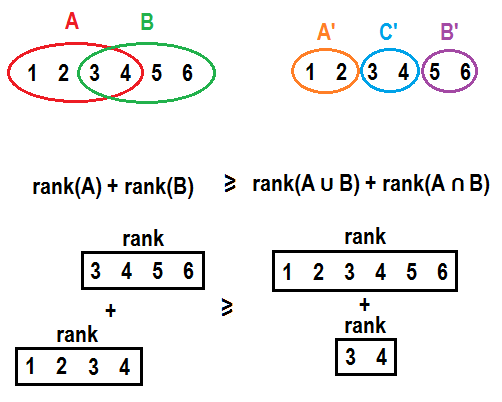
Если говорить совсем просто, принцип “не класть все яйца в одну корзину” работает тут.

Оракул независимости. Говоря о классификации подмножеств, мы обычно не можем позволить себе явно хранить информацию о каждом подмножестве (это потребует экспоненциального размера памяти). Поэтому нам нужны какие-то другие инструменты для проверки отдельных подмножеств на независимость. Если матроид определяется на основании взаимодействия элементов внутри каких-то других структур, то мы обычно (возможно, всегда?) можем найти алгоритм с полиномиальным временем работы, позволяющий проверить какое-либо конкретное подмножество на независимость. Было бы очень удобно обобщить концепцию матроидов и использовать их, не привязываясь при этом к механизмам независимости внутри них. Мы можем определить оракула независимости (independence oracle) как функцию, которая проверяет подмножество на независимость. И теперь мы можем измерять время работы алгоритмов в вызовах оракула (oracle calls). (Однако на практике мы не можем полностью использовать такую абстракцию, потому что тогда мы упустим отличные возможности для оптимизации связанных с этим алгоритмов.)

Примеры

Существуют матроиды различных типов. Вот несколько примеров:

Универсальный матроид. Матроид, который считает подмножество $$$S$$$ независимым, если размер $$$S$$$ не превосходит некоторую константу $$$k$$$ ($$$|S| \leq k$$$). Самый простой, этот матроид никак не различает элементы носителя, ему важно только количество взятых элементов. Все подмножества размера $$$k$$$ являются базисами этого матроида, все подмножества размера $$$(k+1)$$$ являются циклами этого матроида. Можно также определить некоторые специальные случаи универсального матроида:

1. Тривиальный матроид. $$$k = 0$$$. Только пустое множество является независимым, любой элемент носителя является зависимым (и как следствие, любая их комбинация тоже является зависимой).
2. Полный матроид. $$$k = |X|$$$. Все подмножества являются независимыми, включая все множество носитель $$$X$$$.

Линейный матроид (матроид линейной алгебры). Носитель матроида состоит из векторов некоторого векторного пространства. Множество векторов независимо, если оно линейно независимо (никакой из векторов не может быть выражен как линейная комбинация других векторов этого множества). Это тот матроид, с которого началась вся теория матроидов. Линейные базисы множества векторов являются базисами матроида. Любой цикл этого матроида — это множество векторов, где каждый вектор может быть представлен как линейная комбинация остальных векторов, но эта комбинация включает в себя все остальные вектора в цикле. Оракул независимости для этого матроида может быть основан на методе Гаусса.

Цветной матроид. Носитель этого матроида состоит из раскрашенных элементов. Каждый элемент окрашен ровно в один цвет. Множество элементов независимо, если все его элементы имеют различные цвета. Ранг множества в этом матроиде — это количество различных цветов среди его элементов. Базисы этого матроида — это множества, которые содержат ровно один элемент каждого цвета, известного матроиду. Циклы этого матроида — это все возможные пары элементов одинакового цвета. Цвета можно занумеровать целыми числами для практического применения.

Графовый матроид. Этот матроид определен на ребрах неориентированного графа. Множество ребер независимо, если оно не содержит цикл. Это наилучший тип матроидов для демонстрации визуальных примеров потому, что позволяет включать зависимые множества большого размера и в то же время может быть изображен на картинке. Если граф связный, то любой базис этого матроида будет остовным деревом графа. Если граф не связный, то базис будет лесом остовных деревьев, который включает остовное дерево каждой компоненты связности. Циклы такого матроида — это все простые циклы в этом графе. Оракул независимости для этого матроида может быть реализован с помощью DFS, BFS (начать с каждой вершины и проверить что не существует ребра, которое бы вело в уже посещенную вершину) или DSU (объединять соединенные компоненты в графе, начать с отдельных вершин, добавлять все ребра по порядку и проверять, что все ребра на момент добавления соединяют различные компоненты связности). Вот пример свойства комбинации циклов в графовом матроиде:

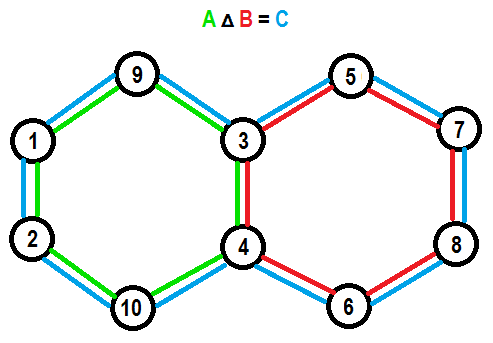
Усеченный матроид. Можно ограничить ранг любого матроида каким-нибудь числом $$$k$$$ без нарушения свойств матроида. Например, базис усеченного цветного матроида — это множество, содержащее не более $$$k$$$ различных цветов и все цвета в нем различны. Базис усеченного графового матроида — это ацикличное множество ребер, которое оставляет в графе не менее $$$(n-k)$$$ компонент связности (где $$$n$$$ — это количество вершин в графе). Это возможно потому, что третье свойство матроидов относится не только к базисам матроидов, но и ко всем независимым подмножествам. И когда все независимые множества размерами больше чем $$$k$$$ одновременно убираются, независимые множества размера ровно $$$k$$$ становятся новыми базисами и для любого меньшего независимого множества мы все еще можем найти элементы из каждого базиса, которые могут быть в него добавлены.

Матроид на подмножестве носителя. Мы можем ограничить носитель матроида до какого-либо его подмножества не ломая свойства матроида. Это возможно потому, что свойства независимости не опираются на отдельные элементы носителя матроида. Так, если удалить ребро из графа, мы все равно получим корректный граф. Если мы удалим один элемент из множества (векторов или цветных элементов), мы все равно получим корректное множество элементов определенного типа и правила независимости сохранятся. Можно также определить ранг подмножества как ранг матроида с носителем усеченным до этого подмножества.

Расширенный матроид. Прямая сумма матроидов. Мы можем рассматривать два отдельных матроида, как один большой матроид без всяких проблем, если элементы носителя первого матроида не оказывают никакого влияния на независимость и не пересекаются с элементами второго матроида и наоборот. Предположим у нас есть два графовых матроида на двух связных графах. Мы можем объединить графы вместе и получить один граф с двумя компонентами связности, но ясно, что включение ребер из одной компоненты связности никак не влияет на наличие или отсутствие цикла в другой компоненте связности. Это называется прямая сумма матроидов (direct matroid sum). Формально, $$$M_1 = \left\langle X_1, I_1 \right\rangle$$$, $$$M_2 = \left\langle X_2, I_2 \right\rangle$$$, $$$M_1 + M_2 = \left\langle X_1 \cup X_2, I_1 \times I_2 \right\rangle$$$, где $$$\times$$$ обозначает декартово произведение двух множеств. Вы можете объединять сколько угодно матроидов каких угодно типов без всяких ограничений. (конечно, если найдете применение для результата).

Это не единственные типы матроидов. Вы можете найти информацию о других типах матроидов или даже создать свои собственные.

Алгоритм Радо-Эдмондса

Теперь поговорим о практических применениях матроидов. У нас есть следующая задача: нужно найти базис матроида $$$M = \left\langle X, I \right\rangle$$$. Как решить ее эффективно?

Согласно третьему свойству матроидов, если у нас есть какое-то независимое множество $$$S$$$ меньшего размера чем базис, мы можем найти какой-то элемент $$$x$$$, который может быть добавлен в $$$S$$$ без потери независимости. Так, мы можем начать с пустого множества, которое точно независимо, и добавлять элементы один за одним, выполняя линейный поиск, чтобы найти следующий элемент, который может быть добавлен. Если обозначить за $$$n$$$ размер носителя $$$X$$$, а за $$$r$$$ обозначить ранг $$$M$$$, то мы получим алгоритм с временем работы $$$\mathcal{O}(r \cdot n)$$$ вызовов оракула.

Мы можем делать это эффективнее, если заметить следующий факт: если какой-то элемент $$$x$$$ не был добавлен в $$$S$$$ на каком-то шагу, то мы ни на одном из следующих шагов не сможем добавить его в $$$S$$$ потому, что если $$$S \cup \{x\}$$$ был классифицирован как зависимый на одном из шагов, то он содержит какой-то цикл $$$C$$$ и так как мы никогда не исключаем элементы из множества $$$S$$$, то на любом следующем шаге $$$S$$$ будет только расширяться и $$$S \cup \{x\}$$$ все так же будет содержать цикл $$$C$$$ и будет зависимым. Так мы можем найти базис матроида за один проход по элементам носителя, если будем брать элементы жадно (включать элемент в $$$S$$$ если это не приводит к потере независимости $$$S$$$ на текущем шагу). Так мы улучшили время работы до $$$\mathcal{O}(n)$$$ вызовов оракула.

А что насчет взвешенного случая? Пусть у каждого элемента носителя $$$x$$$ есть некоторый вес $$$w(x)$$$. Мы хотим найти базис нашего матроида с минимальным суммарным весом его элементов.

Вы возможно знаете про алгоритм Краскала для построения минимального остовного дерева, но как доказать его корректность без привлечения теории матроидов?

Смотря в сторону жадных идей, мы можем попытаться найти какую-нибудь связь между результатами $$$k$$$-й и $$$(k+1)$$$-й стадии алгоритма. Обозначим за $$$A$$$ независимое множество размера $$$k$$$ с минимальным весом и за $$$B$$$ независимое множество размера $$$(k+1)$$$ с минимальным весом. По третьему свойству матроидов, существует хотя бы один элемент $$$y$$$ в $$$B$$$ который может быть добавлен в $$$A$$$ без потери независимости. Так, у нас еще есть $$$2$$$ множества $$$B \setminus \{y\}$$$ размера $$$k$$$ и $$$A \cup \{y\}$$$ размера $$$(k+1)$$$. Так как мы знаем какие из них минимальные, то мы можем записать:

$$$A \leq B \setminus \{y\}$$$

$$$B \leq A \cup \{y\}$$$

добавим $$$y$$$ к двум множествам в первом неравенстве и получим:

$$$A \cup \{y\} \leq (B \setminus \{y\}) \cup \{y\}$$$

$$$A \cup \{y\} \leq B$$$

можно видеть, что

$$$B \leq A \cup \{y\} \leq B$$$

что на самом деле обозначает

$$$B = A \cup \{y\}$$$

Другими словами, мы можем получить независимое множество минимального веса размера $$$(k+1)$$$ из независимого множества минимального веса размера $$$k$$$ добавив в него какой-нибудь элемент $$$y$$$, который не нарушает его независимость. Что если таких элементов $$$y$$$ несколько? Жадный ответ, $$$y$$$ минимального веса.

Объединяя это с предыдущими результатами мы получаем такой алгоритм поиска базиса минимального суммарного веса:

1. Отсортируем элементы носителя матроида по увеличению веса
2. Начнем с пустого множества $$$S$$$
3. Итерируемся по элементам носителя в отсортированном порядке, включая текущий элемент в $$$S$$$, если он не делает $$$S$$$ зависимым

Время работы: $$$\mathcal{O}(n \cdot log(n))$$$ единичных операций для сортировки плюс $$$\mathcal{O}(n)$$$ вызовов оракула.

Это алгоритм Радо-Эдмондса. Как пример для конкретного типа матроидов у нас есть алгоритм Краскала для построения минимального остовного дерева.

Если поиск базиса в любом матроиде осуществляется жадно и матроиды в целом про обобщение вещей, возможно мы можем показать, что все жадные решения сводятся к поиску базиса в каком-нибудь матроиде? Чтож, нет.

В жадных решениях мы можем не только сортировать элементы и рассматривать их по порядку, но и создавать новые элементы на ходу или использовать особые компараторы или условия для взятия или пропуска элементов. Даже если забыть про веса и наложить дополнительные ограничения, мы можем использовать матроиды только в особых случаях. В общем, если мы хотим доказать, что имеем дело с матроидами стоит сфокусироваться на доказательстве их аксиоматических свойств.

Пересечение матроидов

И тут может возникнуть вопрос “Зачем вообще нужны все эти обобщения, если это не привносит ничего нового, ничего такого, что не было бы покрыто более ситуативными и специфичными для своих задач алгоритмами?” Однако, существуют задачи, которые крайне тяжело (на мой взгляд) решить без этих обобщений. Одна из таких задач — это задача о пересечении матроидов.

Более детально, эту задачу стоит называть “поиск наибольшего независимого множества в пересечении двух матроидов”. Формально, дано два матроида $$$M_1 = \left\langle X, I_1 \right\rangle$$$ и $$$M_2 = \left\langle X, I_2 \right\rangle$$$ и мы хотим найти любое множество $$$S$$$ такое, что $$$\max\limits_{S \in I_1 \cap I_2} |S|$$$. Другими словами, наибольшее возможное $$$S$$$, которое признается независимым обоими матроидами.

Можно привести множество примеров таких задач. Мне больше всего нравятся эти:

Цветное остовное дерево. Вам дан граф и для каждого ребра в этом графе задан цвет. Нужно найти остовное дерево в этом графе, в котором нет двух ребер одинакового цвета. Очевидно, матроидные классификации тут “множество ребер содержит не более одного ребра каждого цвета” и “множество ребер не содержит циклов”.

Цветной линейный базис. Задано множество векторов в некотором векторном пространстве и цвет каждого вектора. Нужно найти базис заданного множества векторов, содержащий не более одного вектора каждого цвета. Тут классификациями будут линейная независимость для одного и уникальные цвета для другого матроида.

Максимальное паросочетание в двудольном графе. Хорошо известная задача, задан двудольный граф и необходимо найти такое подмножество ребер максимального размера, что ни одна пара ребер в нем не имеет общей вершины. Возможно тут не очевидно, что мы должны сделать тут, но подумайте в сторону такой более простой версии задачи: заменим “ни одна пара ребер в нем не имеет общей вершины” на “ни одна пара ребер в нем не имеет общей вершины в левой доле”. Теперь мы легко можем решить эту задачу включая в наше множество по одному ребру на каждую вершину ненулевой степени в левой доле, также мы можем показать, что это можно делать жадно и что она образует корректный матроид. И так как у нас есть две части в графе, мы можем сделать еще один матроид для правой части симметрично и решать задачу об их пересечении.

Но подождите, почему обязательно два матроида? Что насчет пересечения большего числа? Чтож, это существенно расширяет ряд задач, которые могут быть сведены к пересечению нескольких матроидов. На самом деле это становится настолько общим, что может предложить решение для задачи о Гамильтоновом пути. Задан ориентированный граф, пересечем эти три матроида на множестве ребер этого графа:

1. Из каждой вершины исходит не более одного ребра (может быть представлен как цветной матроид, покрасим ребра исходящие из одной вершины в один и тот же цвет)
2. В каждую вершину входит не более одного ребра (так же как и предыдущий)
3. Множество ребер не содержит циклов (забудем про ориентацию ребер и проверим, что множество формирует лес остовных деревьев)

И... это NP-полная задача. Что означает у нас нет представления о том, как ее решать за полиномиальное время.

Так, возвращаясь к двум матроидам. Как нам подходить к этой задача? Наивное экспоненциальное решение очевидно (проверим все подмножества из $$$I_1$$$ или $$$I_2$$$). Трудности начинаются из-за того, что $$$\left\langle X, I_1 \cap I_2 \right\rangle$$$ не всегда является корректным матроидом. Как нам известно, базис любого матроида может быть найден жадно, ну а случайно собирать ребра в максимальное паросочетание не очень хорошая идея.

Возможно, вы знаете про алгоритм Куна для построения максимального паросочетания двудольного графа и используя тот факт, что эти задачи похожи, вы возможно как-нибудь сможете прийти к общему решению.

Нам нужны некоторые наблюдения тут. Рассмотрим один матроид $$$M = \left\langle X, I \right\rangle$$$ и какой-нибудь его базис $$$B$$$ (и этот базис не уникален, иначе это будет довольно тривиальный случай). Мы всегда можем найти какой-то элемент $$$p$$$, который можно исключить из $$$B$$$, и какой-то другой элемент $$$q$$$, который может быть добавлен в $$$B$$$ взамен, так что это не нарушит независимость (формально, $$$B \setminus \{p\} \cup \{q\} \in I$$$).

Для примера, рассмотрим графовый матроид $$$M$$$ показанного ниже графа, красные и желтые ребра формируют остовное дерево, которое является базисом в $$$M$$$.

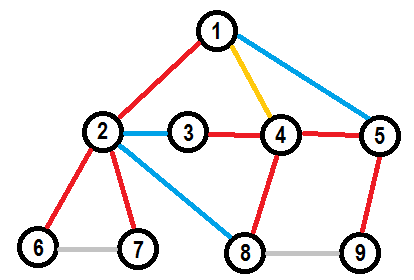
Мы можем заменить желтое ребро на одно из синих ребер чтобы получить остовное дерево отличное одним ребром. Давайте называть эту операцию заменой. Давайте посмотрим, можно ли найти последовательность замен, которые позволят нам заменить базис $$$B$$$ на какой-нибудь другой корректный базис матроида $$$M$$$.

Для примера, вот два различных остовных дерева в том же графе:

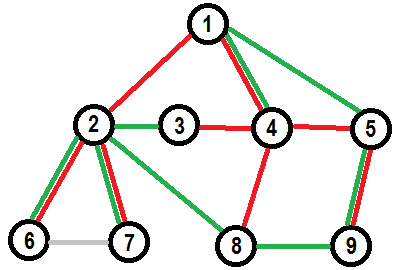
Мы можем получить зеленое дерево из красного такой последовательностью операций замены:

1. Заменить $$$(4,5)$$$ на $$$(1,5)$$$
2. Заменить $$$(4,8)$$$ на $$$(8,9)$$$
3. Заменить $$$(1,2)$$$ на $$$(2,3)$$$
4. Заменить $$$(3,4)$$$ на $$$(2,8)$$$

Стоит заметить, что сами замененные пары, а также их последовательность важны. Мы не можем заменить $$$(3,4)$$$ на $$$(2,8)$$$ раньше чем заменим $$$(1,2)$$$ на $$$(2,3)$$$ так как это приведет к изолированию вершины $$$3$$$ и созданию цикла в другой части графа. Также, мы не можем начать с замены $$$(4, 5)$$$ на $$$(2, 8)$$$.

Оказывается мы всегда можем найти последовательность операций замены, которая позволит нам заменить наш базис $$$B$$$ на любой другой корректный базис матроида $$$M$$$ вне зависимости от его типа. Это свойство называется сильная лемма о замене базиса (“strong basis exchange” lemma) и она может быть строго доказана в общем виде. Можно обобщить эту лемму на замену любых независимых подмножеств равного размера, используя тот факт, что они являются корректными базисами усеченной версии матроида $$$M$$$.

Зная это, было бы неплохо найти какое-нибудь хорошее представление для всех возможных операций замены элементов носителя матроида для конкретного независимого множества $$$S$$$. Возможная операция замены — это взаимосвязь между двумя элементами: $$$x$$$ из $$$S$$$ и $$$y$$$ не из $$$S$$$. Известный факт, графы — это отличный способ представления взаимосвязей между парами элементов. Мы можем определить граф замен $$$D_M (S)$$$ независимого множества $$$S$$$ в матроиде $$$M$$$ как двудольный граф, в котором есть ребро $$$(x, y)$$$ если мы можем заменить $$$x$$$ на $$$y$$$ в $$$S$$$ без потери независимости (формально, $$$D_M (S)$$$ содержит ребро $$$(x, y)$$$ если $$$x \in S, y \in X \setminus S, S \setminus \{x\} \cup \{y\} \in I$$$).

Дальше по тексту я буду называть часть, которая содержит элементы из $$$S$$$, “левой” частью и часть, которая содержит элементы не из $$$S$$$, “правой” (так же будет и на картинках графов замен).

Для примера, вот небольшой граф $$$G$$$, его красное остовное дерево $$$S$$$ и граф замен $$$D_M (S)$$$ в графовом матроиде $$$M$$$ на $$$G$$$:

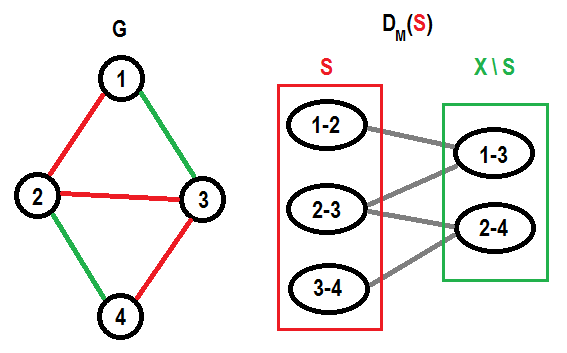
Что граф замен может нам предложить? Во-первых, рассмотрим другое независимое множество $$$T$$$ с таким же размером ($$$|S| = |T|$$$). В $$$D_M (S)$$$ существует идеальное паросочетание между $$$S \setminus T$$$ и $$$T \setminus S$$$ (между элементами, входящими в одно множество, но не входящими в другое и их симметрией). По обобщению леммы о сильной замене базисов мы можем один за одним заменять элементы формируя это идеальное паросочетание по одному ребру.

Однако, обратное утверждение не верно. Мы не можем гарантировать что мы получим независимое множество, если возьмем любое паросочетание в графе замен и выполним замены, связанные с выбранными ребрами. Это очень легко показать для цветного матроида, мы можем заменить любой элемент на элемент не использованного цвета $$$c$$$, но мы не можем заменить два элемента (не цвета $$$c$$$) на два элемента цвета $$$c$$$ одновременно. Для графового матроида есть следующий пример. У нас есть ациклическое множество красных ребер заданного графа:

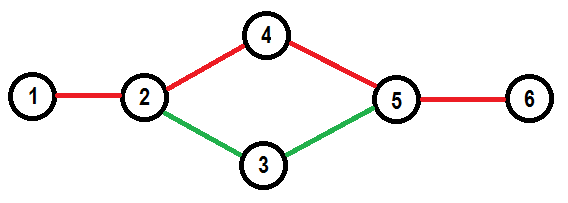
Можно заменить $$$(1, 2)$$$ на $$$(2, 3)$$$, симметрично можно заменить $$$(5, 6)$$$ на $$$(3, 5)$$$. Однако нельзя сделать эти замены одновременно.

Так, как мы можем понять приведут ли какие-то изменения к потере независимости или нет? Можно заметить, что существует несколько способов включить некоторый цикл $$$C$$$ в наше независимое множество $$$S$$$ следуя ребрам замен в $$$D_M (S)$$$. В примере выше мы также можем получить тот же цикл $$$(2-3-5-4)$$$ заменив $$$(5, 6)$$$ на $$$(2, 3)$$$ и $$$(1, 2)$$$ на $$$(3, 5)$$$. Всегда ли это так?

Давайте попробуем построить случай, когда есть ровно один способ получить какое-то зависимое множество следуя ребрам в $$$D_M (S)$$$. Так, нам нужен какой-то цикл $$$C$$$, который бы сформировался в результате замен. Нас не интересуют ребра замен, соединяющие два элемента из $$$C$$$, так как включение любого из них в паросочетание приведет к разрушению $$$C$$$ (у нас нет способа вернуть извлеченный элемент назад). Этот цикл $$$C$$$ должен содержать как минимум $$$2$$$ “вакантных места” в виде элементов, на которые будет происходит замена (для элемента из $$$C$$$ не должны быть в $$$S$$$, $$$|C \setminus S| \geq 2$$$). Если существует только одно “вакантное место”, то в графе замен не будет ребра к этому элементу из любого элемента не из $$$C$$$, так как включение этого элемента приведет к моментальному завершению цикла $$$C$$$ и потере независимости, а это не допускается при построении графа $$$C$$$. Так, мы в целом хотим сделать какую-то структуру такого рода:

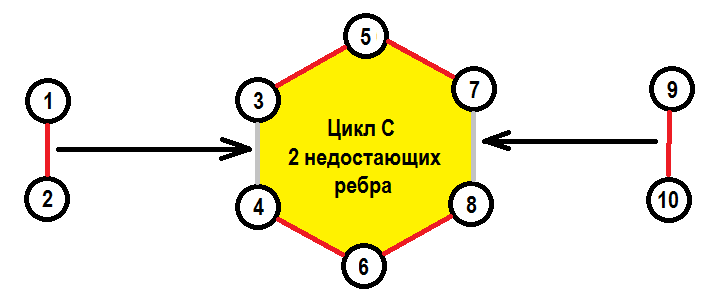
Тут ребра независимого множества $$$S$$$ отмечены красным, а не включенные в $$$S$$$ ребра отмечены серым, запланированные замены ребер показаны черными стрелками. Цикл $$$C$$$ содержит все ребра, образующие границу желтой области ($$$C$$$ — это $$$(3-5-7-8-6-4)$$$). Теперь, существует два способа замены ребер для завершения цикла $$$C$$$. Нам нужно найти способ запретить менять $$$(9, 10)$$$ на $$$(3, 4)$$$ и $$$(1, 2)$$$ на $$$(7, 8)$$$. Единственный способ сделать это в терминах графа замен — это построить дополнительный цикл $$$L$$$ вокруг $$$(3, 4)$$$, который бы содержал $$$(1, 2)$$$ и не содержал $$$(9, 10)$$$, и добавить все ребра $$$L$$$ в $$$S$$$ кроме $$$(3, 4)$$$. Таким образом замена $$$(9, 10)$$$ на $$$(3, 4)$$$ приведет к завершению цикла $$$L$$$, но замена $$$(1, 2)$$$ на $$$(3, 4)$$$ все равно будет возможна. Симметрично, мы можем построить цикл $$$R$$$ вокруг $$$(7, 8)$$$.

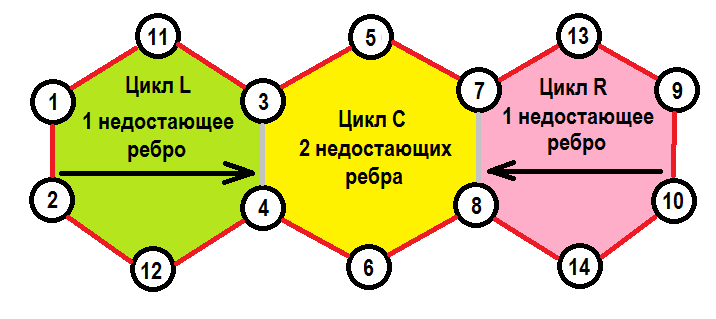
Это оно? Хм, что-то тут пошло не так, так как эти построения привели нас к включению большого цикла из всех красных ребер в $$$S$$$. Но $$$S$$$ должно быть независимым. Это случилось потому, что в терминах линейных комбинаций элемент $$$x$$$ играет такую же роль, как и цикл $$$L$$$, который включает этот элемент $$$x$$$, без этого самого элемента $$$x$$$ ($$$L \setminus \{x\}$$$). Поэтому он и называется циклом. Вершины $$$3$$$ и $$$4$$$ могут быть соединены прямым ребром $$$(3,4)$$$, но также и с помощью другой части цикла $$$L$$$ — $$$(3-11-1-2-12-4)$$$. Увеличение числа элементов из $$$C$$$ не включенных в $$$S$$$ не поможет потому, что нам все равно придется сделать вокруг каждого такого ребра цикл, соединяющий его концы. Изменение типа матроида тоже не поможет, свойства линейных комбинаций сохранятся.

Так, не существует способа ограничить число способов включить цикл $$$C$$$ до одного с помощью ребер графа замен. Это значит, что всегда существует как минимум $$$2$$$ способа включить любой цикл в наше независимое множество используя граф замен. Это также значит, что если существует только один способ получить какое-нибудь другое множество $$$T$$$ из $$$S$$$ используя $$$D_M (S)$$$, то мы можем гарантировать независимость $$$T$$$. Другими словами, мы можем сказать, что $$$T$$$ будет независимым если паросочетание между $$$S \setminus T$$$ и $$$T \setminus S$$$ в $$$D_M (S)$$$ уникально.

Все статьи, которые я видел, доказывают этот факт другим способом, который кажется менее очевидным для меня, но это может быть не так для вас.

Теперь ясно как мы можем стабильно получить другие независимые множества такого же размера. Но нам ведь надо это делать для двух матроидов одновременно, и еще было бы хорошо как-то получить множество максимального размера, а не только того же самого.

Рассмотрим два матроида $$$M_1 = \left\langle X, I_1 \right\rangle$$$ и $$$M_2 = \left\langle X, I_2 \right\rangle$$$ и какое-нибудь множество $$$S$$$ независимое для обоих ($$$S \in I_1 \cap I_2$$$), можно видеть, что графы замен $$$D_{M_1} (S)$$$ и $$$D_{M_2} (S)$$$ имеют те же самые вершины и разбиение на две доли. Это хорошо, эти графы отличаются только ребрами, так мы можем склеить эти графы вместе получив один граф с ребрами двух типов. Будем называть этот граф $$$D_{(M_1, M_2)} (S)$$$. Теперь мы можем сказать, что какое-нибудь множество $$$T$$$ также независимо для обоих матроидов, если существует идеальное паросочетание между $$$S \setminus T$$$ и $$$T \setminus S$$$ для обоих типов ребер в $$$D_{(M_1, M_2)} (S)$$$.

Для примера, рассмотрим задачу о цветном остовном дереве на этом маленьком цветном графе $$$G$$$ и множество графов замен, построенных для цветного остовного дерева $$$S$$$ (его ребра отмечены красным). $$$M_1$$$ обозначает графовый матроид, $$$M_2$$$ обозначает цветной матроид.

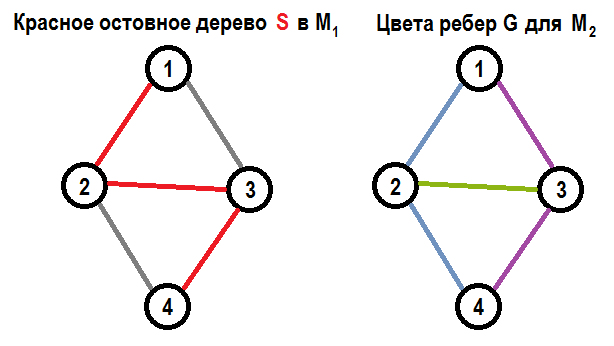
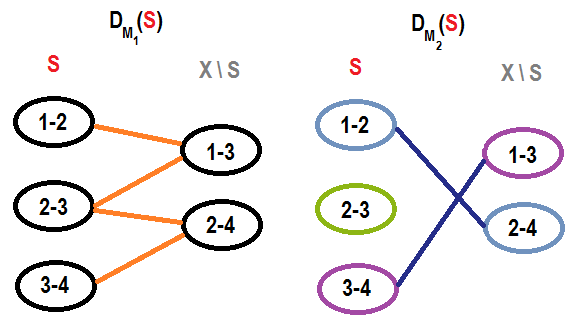
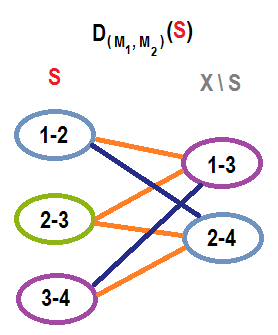
Существует только для цветных остовных дерева в этом графе ($$$S = \{(1, 2), (2, 3), (3, 4)\}$$$ и $$$T = \{(1, 3), (2, 3), (2, 4)\}$$$) и существует идеальное паросочетание между $$$S \setminus T = \{(1, 2), (3,4)\}$$$ и $$$T \setminus S = \{(1, 3), (2, 4)\}$$$ в обоих типах ребер $$$D_{(M_1, M_2)} (S)$$$.

Существует отличный способ найти идеальное паросочетание в двух множествах ребер в двудольном графе. Ориентируем один тип ребер от левой части к правой, а другой тип ребер от правой части части к левой и найдем цикл, содержащий все необходимые вершины. Взгляните на пример:

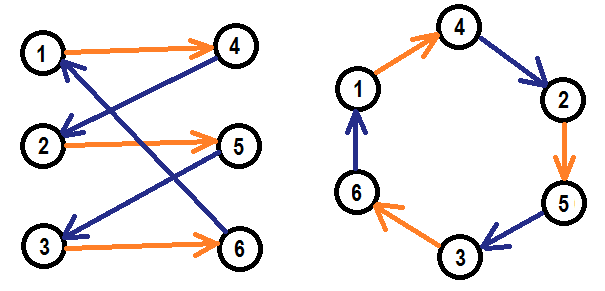
Каждая вершина в цикле касается ровно одного четного ребра и ровно одного нечетного ребра. Ребра в цикле будут иметь их тип в зависимости от их четности. Цикл всегда будет иметь четную длину, так его разложение в два идеальных паросочетания в ребрах разного типа очевидно.

Теперь надо подумать об увеличении размера нашего независимого множества $$$S$$$. В одном матроиде, если независимое множество $$$S$$$ не является базисом, то мы всегда можем найти как минимум один элемент, который можно добавить в $$$S$$$ без потери независимости (по третьему аксиоматическому свойству матроидов). Теперь давайте сгруппируем все элементы, которые могут быть добавлены в него без потери независимости в $$$M_1$$$ в множество $$$Y_1$$$ (формально, $$$x \in Y_1$$$ если $$$x \notin S, S \cup \{x\} \in I_1$$$). Также сгруппируем $$$Y_2$$$ для $$$M_2$$$.

Теперь посмотрим, что можно с этой информацией сделать. Во-первых, если существует элемент $$$x$$$, который входит в оба множества $$$Y_1$$$ и $$$Y_2$$$, то это просто джекпот, идеальный вариант для незамедлительного добавления в $$$S$$$! Во-вторых, если $$$Y_1$$$ пустое или $$$Y_2$$$ пустое, то мы можем сделать вывод, что мы достигли базиса в одном из матроидов и дальнейший рост $$$S$$$ невозможен.

Но это частные случаи, а что делать в общем случае? Ориентируем ребра в $$$D_{(M_1, M_2)} (S)$$$. Ребра из $$$D_{M_1} (S)$$$ направим слева направо, а ребра из $$$D_{M_2} (S)$$$ направим справа налево и найдем... цикл? Нет. Путь из любой вершины $$$Y_1$$$ до любой вершины $$$Y_2$$$. Это послужит сразу двум нашим целям. Но почему и как вообще это должно работать?

Во-первых, выбор пути без возможных сокращений (shortcut) гарантирует нам уникальность паросочетания вдоль пути. До тех пор пока путь можно сократить — используем эту возможность, и в конце у нас окажется путь, где $$$i$$$-ая вершина на пути соединена только с $$$(i+1)$$$-ой и еще возможно с каким-либо подмножеством предыдущих вершин, но это не представляет возможностей для сокращения пути, так как граф ориентирован. Будем называть путь из любой вершины в $$$Y_1$$$ до любой вершины в $$$Y_2$$$ без возможных сокращений аугментирующим путем (augmenting path). Но элементы $$$Y_1$$$ и $$$Y_2$$$ оба находятся в правой доли графа, так длина пути будет нечетной, паросочетание не будет включать все вершины правой доли. Да, это так, но оно будет включать все вершины из левой доли и не будет включать только одну вершину правой доли. Для ребер из $$$D_{M_1} (S)$$$ паросочетание не будет включать первую вершину аугментирущего пути, для ребер из $$$D_{M_2} (S)$$$ последняя вершина пути не будет включена в паросочетание.

И тут в дело вступает наша вторая цель, которой является увеличение размера $$$S$$$. Давайте расширим носитель $$$X$$$ обоих наших матроидов одним элементом $$$t$$$, который будет полностью независим от других элементов для обоих матроидов, и добавим его в $$$S$$$. В $$$D_{M_1} (S)$$$ будут существовать ребра между $$$t$$$ и всеми элементами из $$$Y_1$$$, и аналогично в $$$D_{M_2} (S)$$$ будут существовать ребра между $$$t$$$ всеми элементами из $$$Y_2$$$. Так, мы можем достроить наш аугментирующий путь до цикла, соединив последнюю вершину с $$$t$$$ и $$$t$$$ с первой вершиной. Так, полная картина будет выглядеть примерно так (для ясности, изображены только ребра, включенные в цикл)

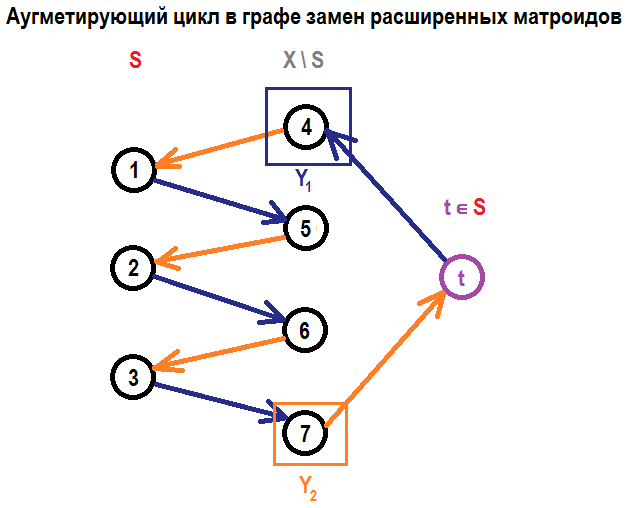
В этом цикле будет уникальное паросочетание, как следствие уникальности паросочетания в выбранном пути, так мы можем совершить ряд замен, ассоциированных с выбранными в цикл ребрами (по сути с выбранными в цикл вершинами). Но мы также включили в наше множество $$$S$$$ временную вершину $$$t$$$, которая будет удалена оттуда после применения всех выбранных замен. Так, мы получили независимое множество $$$S$$$ на расширенных матроидах на без использования временной вершины $$$t$$$, что означает мы можем забыть про $$$t$$$ и сказать, что мы увеличили размер $$$S$$$ на $$$1$$$, выполнив эти операции на исходных матроидах.

Теперь мы установили способ увеличения размера $$$S$$$ на один. Так, мы можем начать с пустого множества $$$S$$$ и выполнять эту операцию до тех пор, пока у нас находится аугметирующий путь.

Хорошо, но что насчет достаточности? Как нам показать, что выполнение этой операции не остановится раньше, чем мы достигнем максимально возможного размера независимого множества? Если одно из множеств $$$Y_1$$$ или $$$Y_2$$$ оказалось пустым, то это значит, что мы достигли базиса в одном из матроидов и это, очевидно, максимум для пересечения матроидов (по третьему аксиоматическому свойству матроидов, мы всегда сможем найти элемент, котрый может быть добавлен в независимое множество, если его размер меньше размера базиса).

Но что насчет случая, когда ни один из базисов еще не достигнут, но мы не смогли найти аугментирующий путь? Нам нужно немного теории тут. Рассмотрим некоторое множество $$$S$$$ независимое для обоих матроидов $$$M_1$$$ и $$$M_2$$$ с ранговыми функциями $$$r_1$$$ и $$$r_2$$$, соответственно. Теперь разделим носитель матроидов $$$X$$$ на две части $$$U$$$ и $$$X \setminus U$$$. Элементы множества $$$S$$$, которые попали в одну и ту же часть при разбиении должны быть независимы для обоих матроидов, говоря в терминах ранговых функций, мы можем записать $$$4$$$ неравенства:

1. $$$|S \cap U| \leq r_1(U)$$$
2. $$$|S \cap U| \leq r_2(U)$$$
3. $$$|S \cap (X \setminus U)| \leq r_1(X \setminus U)$$$
4. $$$|S \cap (X \setminus U)| \leq r_2(X \setminus U)$$$

комбинируя $$$1$$$ и $$$4$$$ мы можем получить

$$$|S \cap U| + |S \cap (X \setminus U)| \leq r_1(U) + r_2(X \setminus U)$$$

$$$|S| \leq r_1(U) + r_2(X \setminus U)$$$

рассматривая все возможные разбиения (все возможные $$$U$$$) и независимое множество $$$S$$$ максимального размера мы получаем

$$$\max\limits_{S \in I_1 \cap I_2} |S| \leq \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$$$

Выглядит немного запутано, но мы мы ввязываемся во все эти сложности чтоб показать достижение какого-то предела. Если мы сможем доказать получение равенства из этого неравенства, то это подтвердит достижение предела и то, что мы не можем получить результат лучше. Так, мы хотим показать:

$$$\max\limits_{S \in I_1 \cap I_2} |S| = \min\limits_{U \subseteq X} (r_1(U) + r_2(X \setminus U))$$$

Этот теоретический предел известен как теорема Эдмондса-Лоулера (Edmonds-Lawler theorem) или как min-max соотношение для пересечения матроидов.

Заметьте, у нас теперь равенство и мы можем не обращать внимания на минимум в правой части, нам достаточно найти любое разбиение $$$U$$$, которое удовлетворит равенство (по сути, это и будет тем минимумом потому, что правая часть не может быть меньше левой). Мы хотим рассмотреть случай, когда у нас нет пути из $$$Y_1$$$ в $$$Y_2$$$, так было бы логично рассмотреть разбиение, основанное на достижимости $$$Y_2$$$. Пусть вершина $$$x$$$ будет лежать в $$$U$$$ если существует путь из вершины $$$x$$$ до любой из вершин в $$$Y_2$$$. Теперь мы можем разбить части равенства назад:

$$$|S| = |S \cap U| + |S \setminus U| = r_1(U) + r_2(X \setminus U)$$$

в

$$$|S \cap U| = r_1(U)$$$

$$$|S \setminus U| = r_2(X \setminus U)$$$

Предположим $$$r_1(U) > |S \cap U|$$$, это будет означать, что существует другое независимое множество $$$T$$$ в $$$U$$$, которое имеет больший размер чем $$$S \cap U$$$. По свойствам матроидов, существует элемент $$$x$$$ в $$$T$$$, который может быть добавлен к $$$S \cap U$$$ без потери независимости в $$$M_1$$$, обобщая $$$U$$$ до $$$X$$$ мы не можем гарантировать, что $$$S \cup \{x\}$$$ будет независимым в $$$M_1$$$, но оно будет включать максимум один цикл $$$C$$$, в котором будет другой элемент $$$y$$$ не из $$$U$$$ (иначе мы не можем гарантировать существование большего независимого множества $$$T$$$ в $$$U$$$). Если цикла $$$C$$$ нет, то любой элемент $$$y$$$ не из $$$U$$$ может быть заменен на $$$x$$$. Но все это означает, что существует ребро $$$(y, x)$$$ в графе замен $$$D_{(M_1, M_2)} (S)$$$, что в свою очередь означает, что мы можем достичь $$$Y_2$$$ из $$$y$$$ через это ребро и вершину $$$x$$$, но мы сделали предположение, что $$$y$$$ не лежит в $$$U$$$, и не существует пути из $$$y$$$ в $$$Y_2$$$. Так мы получили противоречие, что подтверждает $$$r_1(U) = |S \cap U|$$$.

Симметрично, мы можем доказать, что $$$r_2(X \setminus U) = |S \setminus U|$$$.

Эти противоречия изображены на картинках графов замен ниже. Множество $$$U$$$ разбивает носитель $$$X$$$ на две части (над фиолетовой линией и под ней), вершина в $$$Y_2$$$ может быть достигнута из каждой вершины под линией и не может быть достигнута ни из одной вершины над линией. Другими словами, не существует ребер, которые идут из верхней части в нижнюю часть, пересекая фиолетовую линию, что показывает невозможность существования красного ребра.

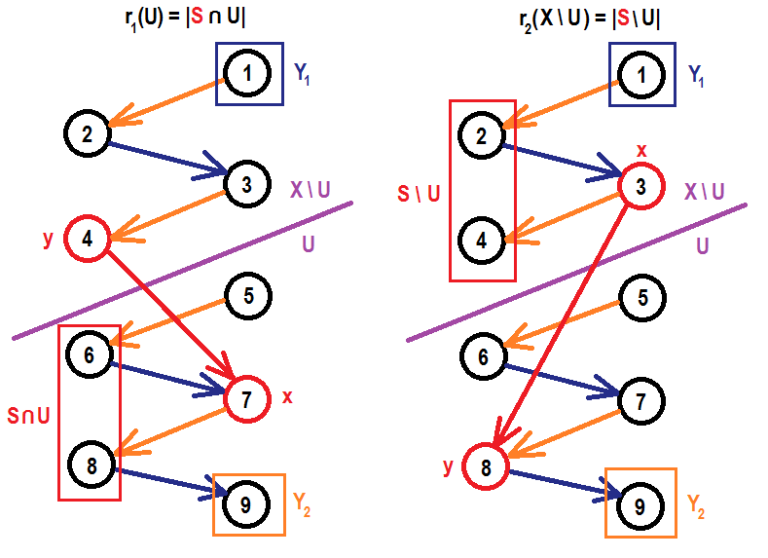
Доказав два эти равенства, мы доказали теорему Эдмондса-Лоулера и доказали, что этот алгоритм всегда достигает оптимального решения.

Пересечение матроидов может быть обобщено на взвешенный случай. И еще есть очень много интересных связанных с этим вещей, которые бы стоило упомянуть, но эта теоретическая часть и без того уже огромная и я не хочу делать делать ее еще больше. Обратитесь к ресурсам из “Полезных ссылок” для дополнительной информации.

Реализация и сложность, оракулы

Теперь у нас есть вся необходимая теория для реализации решения задачи о пересечении матроидов.

Напомню, нам заданы два матроида $$$M_1 = \left\langle X, I_1 \right\rangle$$$ и $$$M_2 = \left\langle X, I_2 \right\rangle$$$ с ранговыми функциями $$$r_1$$$ и $$$r_2$$$ соответственно и оракулы независимости с временами работы $$$C_1$$$ и $$$C_2$$$ соответственно. Нам нужно найти наибольшее множество $$$S$$$, которое будет независимо для обоих матроидов.

Согласно нашему алгоритму нам нужно начать с пустого множества $$$S$$$ и замет повторять следующий процесс до тех пор пока это возможно:

1. Построить граф замен $$$D_{(M_1, M_2)} (S)$$$
2. Найти “свободные для включения” множества $$$Y_1$$$ и $$$Y_2$$$
3. Найти аугментирующий путь $$$P$$$ без возможных сокращений из любого элемента $$$Y_1$$$ в любой элемент $$$Y_2$$$
4. Изменить включение всех элементов пути $$$P$$$ в $$$S$$$

Пусть $$$r$$$ будет размером результата, $$$r = |S|$$$, а $$$n$$$ будет размером носителя, $$$n = |X|$$$. Мы можем наложить верхние ограничения на $$$r \leq min(r_1(X), r_2(X))$$$ потому, что общее независимое множество не может быть больше чем базис каждого из пересекаемых матроидов. Так, основной цикл (процесс аугментации) выполнится $$$r$$$ раз.

На каждой итерации у нас есть $$$4$$$ шага:

1. Построение графа замен это по сути проверка наличия все ребер в двудольном графе с разбиением $$$S$$$ и $$$X \setminus S$$$. Мы можем оценить размеры долей как $$$|S| = \mathcal{O}(r)$$$ и $$$|X \setminus S| = \mathcal{O}(n)$$$. Между каждой парой вершин из разных долей может быть два ребра (одно слева направо, другое справа налево). Проверка их наличия требует $$$1$$$ вызова оракула у обоих матроидов. Так, проверка наличия всех ребер требует $$$\mathcal{O}(r) \cdot \mathcal{O}(n) \cdot (C_1 + C_2) = \mathcal{O}(r \cdot n \cdot (C_1 + C_2))$$$.
2. Построение $$$Y_1$$$ требует $$$1$$$ вызова оракула первого матроида на каждую из вершин правой доли $$$X \setminus S$$$, это дает время работы $$$\mathcal{O}(n \cdot C_1)$$$. Симметрично, построение $$$Y_2$$$ требует $$$1$$$ вызова оракула второго матроида на каждую из вершин правой доли $$$X \setminus S$$$, что дает время работы $$$\mathcal{O}(n \cdot C_2)$$$. Комбинируя их вместе, мы получаем $$$\mathcal{O}(n \cdot (C_1 + C_2)).$$$
3. Хм, поиск “пути без возможных сокращений”. Кратчайший путь сгодится. Так, тут нам нужен поиск в ширину. Время работы $$$\mathcal{O}(V + E) = \mathcal{O}(n + r \cdot n) = \mathcal{O}(r \cdot n).$$$
4. Это самая быстрая часть. Размер кратчайшего пути не может превышать количество вершин в графе. Время работы $$$\mathcal{O}(n)$$$.

Без каких-либо оптимизаций, затрагивающих несколько шагов алгоритма мы получаем общее время работы $$$\mathcal{O}(r^2 \cdot n \cdot (C_1 + C_2))$$$. Что в целом уже неплохо для некоторых задач, но мы точно можем достичь лучшего результата.

Легко увидеть, что самым тяжелым местом этого алгоритма является шаг $$$1$$$. Можно заметить, что этот шаг не требует проверки независимости произвольных множеств. Нам нужно только взять некоторые независимое множество $$$S$$$ и заменять одну пару его элементов единовременно. В целом нам нужно только удалять максимум один элемент и добавлять максимум один элемент и затем проверять независимость.

Мы можем найти оптимизированные решения для разных типов матроидов:

Цветной матроид. У нас есть элементы различных цветов, проверить что у нас не более $$$1$$$ элемента каждого цвета одновременно. Количество различных цветов не может превышать $$$n$$$, мы можем использовать массив количеств, который позволит за $$$\mathcal{O}(1)$$$ сообщать нам количество элементов $$$i$$$-го цвета, добавлять и удалять элементы. Нам в целом больше тут ничего делать и не нужно, проверка за $$$\mathcal{O}(1)$$$ очевидная комбинация этих операций.

Графовый матроид. У нас есть лес остовных деревьев, нам нужно проверить что замена пары ребер не создает цикл.

Мы можем $$$r$$$ раз удалить одно ребро, подсчитать компоненты связности и для каждой из вершин найти номер ее компоненты связности за $$$\mathcal{O}(n)$$$, и потом мы можем добавить ребро только в случае, если оно соединяет вершины из разных компонент связности. Это требует $$$\mathcal{O}(r \cdot n)$$$ на подготовку и позволяет проверять наличие ребра за $$$\mathcal{O}(1)$$$. Отличный баланс между частью преподсчета и запросами существования ребер, но в целом не представляет возможности что-то улучшить дальше и, кажется что, требует $$$\mathcal{O}(r \cdot n)$$$ памяти.

Мы можем попробовать другой подход. Если добавляемое ребро соединяет два различных остовных дерева, то оно не нарушает независимость. Если оно соединяет две вершины в одном дереве, то оно образует цикл, и нам нужно удалить одно из ребер на этом цикле. Так, если мы добавили ребро $$$(x, y)$$$, то нас устроит только удаление какого-либо другого ребра на уникальном пути в дереве между $$$x$$$ и $$$y$$$. Мы можем свести задачу проверки наличия ребра в графе замен к одному запросу проверки, что ребро $$$(x, y)$$$ лежит на пути между вершинами $$$a$$$ и $$$b$$$. Это можно делать с помощью бинарных подъемов (binary lifting), получая время работы $$$\mathcal{O}(n \cdot log(n))$$$ на преподсчет и $$$\mathcal{O}(log(n))$$$ на проверку одного ребра. Потребление памяти может быть уменьшено до $$$\mathcal{O}(n \cdot log(n))$$$.

Я не проверял какой из подходов на практике лучше. Я думаю, что первый подход должен давать лучшие результаты до тех пор пока ограничение по памяти не является проблемой.

Линейный матроид. У нас есть независимое множество векторов в каком-нибудь векторном пространстве. Нам нужно проверять можем ли мы удалить один из векторов и добавить другой. Общий подход — это метод Гаусса, хорошо известное время работы $$$\mathcal{O}(r^2 \cdot m)$$$, где $$$m$$$ это количество измерений векторного пространства. Если векторное пространство имеет вид $$$\mathbb{Z}_2^m$$$ мы можем применить оптимизацию битсетами и получить $$$\mathcal{O}(\frac{r^2 \cdot m}{w})$$$, где $$$w$$$ — это размер машинного слова. Но мы можем проверять потерю независимости после добавления одного вектора к множеству быстрее, если у нас есть посчитанный базис этого множества. Это можно делать за $$$\mathcal{O}(r \cdot m)$$$ потому, что нам нужно только “занулить” один вектор. Мы не можем найти способ удалить вектор из множества после применения метода Гаусса к нему (я думаю, что-нибудь для этого все же сделать возможно, но это не будет легко и быстро). Но мы можем преподсчитать базисы для каждого вектора, который собираемся удалять и потом будем только пробовать “обнулить” один вектор, вместо преобразования всех векторов множества. Так мы можем получить время работы $$$\mathcal{O}(r^3 \cdot m)$$$ на преподсчет и $$$\mathcal{O}(r \cdot m)$$$ на проверку одного ребра.

Но специфичные для алгоритма оракулы — это не единственная возможная оптимизация тут.

Можно заметить, что роли матроидов в пересечении не совсем симметричны. Но это не имеет значения для решения задачи. Так, мы можем попробовать поменять местами $$$M_1$$$ и $$$M_2$$$, и это может повлиять на время работы решения.

Для поиска кратчайшего пути в графе нам в целом не обязательно знать всю его структуру. Если наши оракулы не получают выгоду от построения всего графа замен целиком, то мы можем строить его лениво: можно проверять наличие ребра только в тот момент, когда BFS пытается использовать их. Можно подумать, что это лишь улучшает константу, но статья, указанная в ссылках под номером $$$3$$$, содержит это:

Cunningham has shown that we can find a maximum independent set with $$$\mathcal{O}(r^{1.5} \cdot n)$$$ oracle calls. The idea is to take a shortest augmenting path each time.

Оказывается, что эта оптимизация на самом деле улучшает сложность алгоритма. В общем нам потребуется в $$$\mathcal{O}(\sqrt{r})$$$ раз меньше вызовов оракулов, если мы будем строить графы замен лениво.

Задача “Pick Your Own Nim“

К сожалению, я знаю только одну задачу, которая напрямую требует алгоритмов работающих непосредственно с матроидами. Я не беру в рассчет приложения алгоритма Радо-Эдмондса и использование теории матроидов в доказательствах корректности.

Если вы знаете интересные задачи о матроидах, будет отлично, если поделитесь ими в комментариях.

Это задача 102156D - Выбери свой Ним из 2019 Petrozavodsk Winter Camp, Yandex Cup.

У задачи английское условие.

В кратце, задача дает нам несколько коробок с числами и просит нас выбрать ровно одно число из каждой коробки так, что мы не можем выбрать непустое подмножество выбранных чисел с xor-суммой равной $$$0$$$. Или сказать что это невозможно. (Условие включает в себя информацию об игре Ним и теории Шпрага-Гранди, но вся необходимая информацию также дана в условии и нам не надо думать об этом.)

Основное наблюдение заключается в следующем: мы не можем выбрать подмножество с нулевой xor-суммой тогда и только тогда, когда все числа формируют независимое множество как вектора в $$$\mathbb{Z}_2^{60}$$$. Теперь сведение задачи к пересечению матроидов становится очевидным:

1. мы хотим чтоб наше множество чисел было линейно независимо независимо. Так мы можем использовать линейный матроид
2. мы хотим выбрать ровно одно число из каждой коробки. Цветной матроид с этим справится: покрасив все элементы из одной коробки в одинаковый цвет, а элементы из разных коробок в разные цвета.

Теперь мы можем найти наибольшее независимое множество для двух матроидов и проверить, что мы использовали все цвета.

Так это пример задачи о цветном линейном базисе. С некоторыми оптимизациями мы можем решить ее за $$$\mathcal{O}(\frac{r^4 \cdot 60}{w} + \frac{r^{2.5} \cdot 60 \cdot n}{w})$$$. Беря во внимание, что $$$\frac{60}{w}$$$ это $$$1$$$ или очень маленькая константа,мы можем упростить это до $$$\mathcal{O}(r^4 + r^{2.5} \cdot n)$$$. С ограничениями $$$r \leq 60, n \leq 5000$$$ это порядка $$$10^7$$$ операций.

#include <bits/stdc++.h>

using namespace std;

typedef long long int Z2Vector;

struct GroundSetElement {
    int color;
    Z2Vector vector;
    bool in_independent_set;
    int independent_set_position;
    int bfs_parent;
};

struct Z2Basis {
    vector<Z2Vector> vectors;

    void add_vector(Z2Vector new_vector) {
        vectors.push_back(new_vector);
    }

    void reset() {
        vectors.clear();
    }

    int size() {
        return vectors.size();
    }

    void gaussian_elimination() {
        for (int i = 0; i < size(); i++) {
            for (int j = i; j < size(); j++) {
                if (vectors[i] < vectors[j]) swap(vectors[i], vectors[j]);
            }

            for (int j = i+1; j < size(); j++) {
                vectors[j] = min(vectors[j], vectors[j] ^ vectors[i]);
            }
        }
    }

    bool independent_with(Z2Vector new_vector) {
        for (auto v : vectors) new_vector = min(new_vector, new_vector ^ v);

        return new_vector > 0;
    }
};

int n;
int m;

int color_count;
bool color_used[60+60];

vector<GroundSetElement> ground_set;
vector<int> independent_set; /// as indexes of ground set
Z2Basis basis; /// of independent set
Z2Basis basis_without[60+60];

bool linear_oracle(int inserted) {
    return basis.independent_with(ground_set[inserted].vector);
}

bool linear_oracle(int inserted, int removed) {
    int wi = ground_set[removed].independent_set_position;

    return basis_without[wi].independent_with(ground_set[inserted].vector);
}

void prepare_linear_oracle() {
    basis.reset();

    for (int i = 0; i < independent_set.size(); i++) {
        basis_without[i].reset();
    }

    for (int i = 0; i < independent_set.size(); i++) {
        basis.add_vector(ground_set[independent_set[i]].vector);
        for (int  j = 0; j < independent_set.size(); j++) {
            if (i != j) basis_without[j].add_vector(ground_set[independent_set[i]].vector);
        }
    }

    basis.gaussian_elimination();
    for (int i = 0; i < independent_set.size(); i++) {
        basis_without[i].gaussian_elimination();
    }
}

bool colorful_oracle(int inserted) {
    int inserted_color = ground_set[inserted].color;

    return !color_used[inserted_color];
}

bool colorful_oracle(int inserted, int removed) {
    int inserted_color = ground_set[inserted].color;
    int removed_color = ground_set[removed].color;

    if (!color_used[inserted_color]) return true;

    return inserted_color == removed_color;
}

void prepare_colorful_oracle() {
    for (int c = 0; c < color_count; c++) {
        color_used[c] = false;
    }

    for (auto idx : independent_set) {
        color_used[ground_set[idx].color] = true;
    }
}

bool augment() {
    prepare_linear_oracle();
    prepare_colorful_oracle();

    const int SOURCE = -1;
    const int NOT_VISITED = -2;
    const int NOT_FOUND = -3;

    for (int i = 0; i < ground_set.size(); i++) {
        ground_set[i].bfs_parent = NOT_VISITED;
    }

    int endpoint = NOT_FOUND;

    queue<int> q;

    for (int i = 0; i < ground_set.size(); i++) {
        if (colorful_oracle(i)) {
            ground_set[i].bfs_parent = SOURCE;
            q.push(i);
        }
    }

    while (q.size()) {
        int cur = q.front();
        q.pop();

        if (ground_set[cur].in_independent_set) {
            for (int to = 0; to < ground_set.size(); to++) {
                if (ground_set[to].bfs_parent != NOT_VISITED) continue;
                if (!colorful_oracle(to, cur)) continue;

                ground_set[to].bfs_parent = cur;
                q.push(to);
            }
        } else {
            if (linear_oracle(cur)) {
                endpoint = cur;
                break;
            }

            for (auto to : independent_set) {
                if (ground_set[to].bfs_parent != NOT_VISITED) continue;
                if (!linear_oracle(cur, to)) continue;

                ground_set[to].bfs_parent = cur;
                q.push(to);
            }
        }
    }

    if (endpoint == NOT_FOUND) return false;

    do {
        ground_set[endpoint].in_independent_set ^= true;
        endpoint = ground_set[endpoint].bfs_parent;
    } while (endpoint != SOURCE);

    independent_set.clear();
    for (int i = 0; i < ground_set.size(); i++) {
        if (ground_set[i].in_independent_set) {
            ground_set[i].independent_set_position = independent_set.size();
            independent_set.push_back(i);
        }
    }

    return true;
}

void solve() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        ground_set.emplace_back();
        ground_set.back().color = i;
        ground_set.back().in_independent_set = false;

        cin >> ground_set.back().vector;
    }

    cin >> m;
    for (int i = 0; i < m; i++) {
        int k;
        cin >> k;
        while (k--) {
            ground_set.emplace_back();
            ground_set.back().color = n+i;
            ground_set.back().in_independent_set = false;

            cin >> ground_set.back().vector;
        }
    }

    color_count = n+m;

    while (augment()) ;

    if (independent_set.size() < color_count) {
        cout << "-1\n";
        return;
    }

    for (int i = n; i < ground_set.size(); i++) {
        if (ground_set[i].in_independent_set) cout << ground_set[i].vector << "\n";
    }
}

int main() {
    solve();
}

Полезные ссылки

Разумеется, всю информацию можно найти в google запросами вроде “matroid”, “matroid theory”, “matroid intersection” и “matroid intersection algorithm”. Но я перечислю все важные источники информации, которые больше всего помогали мне изучать матроиды и подготовить эту статью.

1. Английская страница матроид на Википедии. Английская версия этой страницы содержит очень много информации про определения, примеры и связанные задачи. Русская версия содержит меньше информации.
2. Категория Матроиды на Вики NEERC IFMO из более 20 полезных статей. Некоторые из них не объясняют вещи детально, включая только самые важные пункты, но там можно найти много отличных картинок связанных с этой темой.
3. Конспект лекций MIT про пересечение матроидов, включающий всю теорию, необходимую для построения и доказательства оптимальности алгоритма пересечения матроидов, также время работы этого алгоритма и оптимизацию Cunningham’a. Включает дополнительную информацию про взвешенный случай и про объединение матроидов.
4. Еще конспект лекций MIT про пересечение матроидов, но этот более теоретический и отличается от предыдущего.
5. Статья, которая содержит длинное и загруженное формулами доказательство из начала этой статьи.

Спасибо за прочтение. Я надеюсь, что эта статья окажется полезной тем, кто хочет познакомиться с теорией матроидов в спортивном программировании.