Tutorial for problem "E. Tricky and Clever Password"
Scheme of the author solution
The author solution has the following scheme. Let's brute over each possible position pos of the center of the middle part (the part that must be palindrome by problem statement). Then let's take as a middle the maximum palindrome among all centered in the position pos. After that we have to take as prefix and suffix such maximum-sized substrings, which satisfy all problem constraints, and don't intersect with medium part.
After we do these calculations for each possible position pos, the answer to the problem will be just maximum among answers found on each step.
Efficient Implementation
In fact, the problem consists of two sub-problems:
First, it's a search for a maximum-length palindrome, having its center in the given position pos. We can calculate these answers in O(n) with Manacher's algorithm, which is described on my site (unfortunately, the article is only in Russian, so you have to use Google Translator or something like this). Alternatively you can calculate this "palindromic array" using binary search and, for example, hashes or suffix array: let's search for maximum palindrome length using binary search, then inside the binary search we have to compare for equivalence two substrings of the given string, which can be done in O(1) using hashes or calculated suffix array.
Second, it's a search for maximum length and corresponding positions for prefix and suffix parts, not intersecting the given substring [l;r]. Let's look at lengths sufflen of suffix suffix in order of their increase, then for each fixed sufflen obviously it is the best to look only at first occurence of string prefix = reverse(suffix). Thereby, by increasing the length sufflen, we can move the corresponding prefix only to the right, not to the left. Designating by lpos[sufflen] the position of first occurence of string reverse(suffix(sufflen)) in the given string, we get that these lpos values are non-decreasing. It will be more comfortable to introduce another array rpos[len] = lpos[len] + len - 1 - end-position of occurence of this suffix (obviously these values will strictly increase).
So, if we knew the values of the array lpos (or, more convenient, of the array rpos), then in the main solution (in the place, where after selecting maximum in pos palindrome we have to search for maximum appropriate prefix and suffix) we can use binary search over the length sufflen. Moreover, we can just precalculate answers to each of query of this form, and after that we'll answer to each query in O(1).
The last thing is to learn how to build lpos array - array of positions of first occurences of reversed suffixes.
For example, this can be done using hashes or suffix array. If we've calculated the value lpos[k], let's learn how to calculate lpos[k + 1]. If the substring s.substr(lpos[k], k + 1) equals to s-th suffix of length k + 1, then lpos[k + 1] = lpos[k]. In the other case, we try to increase lpos[k + 1] by one, and again do the comparison, and so on. Comparison of any two substrings can be done in O(1) using hashes or suffix array. Of course, total time to build lpos array will be then O(n) - because there won't be more than n increases (and string comparisons) during the whole algorithm.
Another approach to building lpos array is to use prefixe-function. For this, let's make a string reverse(s) + # + s, and if in some point of the right half of the string the value of the prefix function equaled to k, then let's assign lpos[k] = this position (if, of course, this lpos[k] haven't yet been assigned before - because we have to find only first occurences).
Finally, it's rather easy to get O(n) solution of this problem using rather famous approaches: hashes, suffix array, prefix-function and palindromic array.  -solution is somewhat easier, - it is based on binary search (for building palindromic array and for answering the queries) and, for example, hashes (for comparison of two substrings).
-solution is somewhat easier, - it is based on binary search (for building palindromic array and for answering the queries) and, for example, hashes (for comparison of two substrings).
Proof
The only non-obvious thing is why after we've fixed the position pos (we remind it's a position of middle of central part of middle), - after that we can greedily take the maximum palindrome with center in it.
Let's suppose the contrary: suppose it was better not to take the maximum palindrome centered in pos, but to take some smaller palindrome centered here. Look what happens when we decrease a length of palindrome by two (by one from each end): we loose two symbols in middle, but instead we get more "freedom" for prefix and suffix parts. But for both of them their freedom increased only by one: prefix gained one symbol after the end, and suffix - one symbol before this beginning. So, taking into account the monotonic increase of rpos, we see that prefix and suffix could increase only by one, not more. Summarizing this discussion, we can say that after decreasing the middle part we loose two symbols, and gain maximum two symbols. That's why there is no need in decreasing the middle part, we can always select it as the maximum-sized palindrome.
Another approach
Let's iterate over each suffix length, and after we've fixed some suffix length, we have to find maximum-sized palindrome between the suffix and the found prefix (position of the prefix still has to be found, just like in the previous solution).
First idea is to use some greedy (similar to described above): take maximum-sized palindrome with center between prefix and suffix, and "cut" it down, in order to fit between the prefix and suffix. It's wrong: there are tests, where after cutting the maximum palindrome becomes very small, so after cutting down it's better to choose another palindrome.
But we can cope with this using the following approach: let's find the length of middle part using binary search. To do this, we have to answer the following queries: "is there a palindrome of length at least x among all palindromes centered between l and r". I.e. given x, we should answer, is there a number greater that or equal to x in the segment [l + x;r - x] (I suppose that x is a half of the length of palindrome).
We can answer to these maximum queries using segment tree in 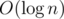 , so the total solution is
, so the total solution is 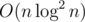 . Alternatively we can use sparse-table to reach
. Alternatively we can use sparse-table to reach 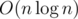 asymptotics (sparse-table is a table where for each position i and power of two j the answer for segment [i;i + j - 1] is precalculated).
asymptotics (sparse-table is a table where for each position i and power of two j the answer for segment [i;i + j - 1] is precalculated).
This can be done using segment tree, built over the palindromic array (the palindromic array should be calculated, as described in the previous solution).











Fuh, so many characters :)
Excuse me for my bad English ;)