A month ago IZhO 2020 was held in Almaty, Kazakhstan. Thanks to Tima we can submit our solutions here. Here is editorial for problems day1 A, day1 B, day2 C. Please write solutions for other problems in comments.
Benq has published his codes for all problems here.
$$$a1$$$ $$$a2$$$ $$$a3$$$ $$$x$$$ $$$a5$$$ $$$a6$$$ $$$a7$$$
$$$b1$$$ $$$b2$$$ $$$b3$$$ $$$y$$$ $$$b5$$$ $$$b6$$$ $$$b7$$$
Lets assume numbers in position $$$i = 4$$$` $$$x$$$ and $$$y$$$ are swaped. $$$y$$$ may go to positions $$${4, 5, 6, 7}$$$. $$$y$$$ can't go to positions $$${1, 2, 3}$$$ cause $$$y > x >= a3 >= a2 >= a1$$$. Similarly $$$x$$$ may go to positions $$${1, 2, 3, 4}$$$ but can't go to positions $$${5, 6, 7}$$$. Its easy to see that still $$$a_1 <= b_1, a_2 <= b_2, a_3 <= b_3$$$, furthermore $$$a_4 <= b_4$$$ $$$=>$$$ Next swap will occurr in $$$j$$$, where $$$j > i$$$.
Now we need a data structure with fast $$$insert$$$, $$$erase$$$ and $$$get minimum$$$ operations. In C++ we have $$$std::multiset<int>$$$. We'll maintain two of them` $$$A$$$ and $$$B$$$. Lets iterate over positions $$$1, 2, ..., n$$$ in this order. When we get to position $$$i$$$, $$$A$$$ must contain $$$a_i, a_{i+1}, ..., a_n$$$, $$$B$$$ must contain $$$b_i, b_{i+1}, ..., b_n$$$. Note: $$$A.min$$$ is equal to $$$b_i$$$, $$$B.min$$$ is equal to $$$a_i$$$.
If $$$A.min > B.min$$$ we must swap $$$a_i$$$ and $$$b_i$$$. Lets erase $$$B.min$$$ from $$$B$$$, insert it into $$$A$$$. Erase $$$A.min$$$ and insert it into $$$B$$$. We know that next swap will occurr at position $$$j$$$, $$$j > i$$$ so we are done with position $$$i$$$. If $$$A.min <= B.min$$$ we are finished, too. So we just erase $$$A.min$$$ from $$$A$$$. $$$A.min$$$ is $$$a_i$$$ thus we are left with numbers $$$a_{i+1}, a_{i+2}, ..., a_n$$$. Do the same with $$$B$$$.
Now we must just count swaps and print it.
Reversing row $$$i$$$ $$$<=>$$$ reversing row $$$n - i + 1$$$
$$$i <= n / 2$$$ or $$$n - i + 1 <= n / 2$$$
Thus we can assume that we will only reverse rows $$$1, 2, ..., n / 2$$$. Similarly we will only reverse rows $$$1, 2, ..., m / 2$$$.
Lets observe cells $$$a[i][j], a[i][m - j + 1], a[n - i + 1][j], a[n - i + 1][m - j + 1]$$$, marked as $$$1, 2, 3, 4$$$ in the following picture.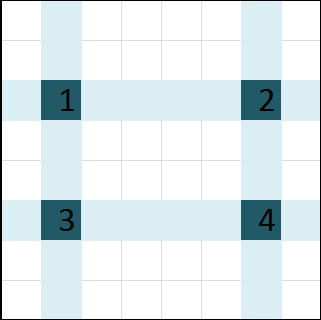
$$$1, 2, 3, 4$$$ will move only among themselves.
Reversing row/column $$$i$$$ twice $$$<=>$$$ not reversing it at all. Thus we will reverse a row/column once or not reverse it at all.
Lets observe all pairs $$$(i, j), i <= n / 2, j <= m / 2$$$. Lets look at 4 options of reversing/not reversing i/j(e.g. reversing $$$i$$$, not reversing $$$j$$$). Only options that put $$$a[i][j], a[i][n - j + 1], a[n - i + 1][j], a[n - i + 1][n - j + 1]$$$ in their right positions are acceptable. Observe different cases and you will see that only following scenarios are possible.(state of row/column $$$i$$$ shows whether $$$i$$$ is reversed or not)
1) Row i must be reversed/not reversed. We can determine state of row i.
2) Column j must be reversed/not reversed. We can determine state of column j.
3) i_is_reversed must be equal to j_is_reversed. Lets connect row $$$i$$$ and column $$$j$$$ with an unordered edge of first type.
4) i_is_reversed can't be equal to j_is_reversed. Lets connect row $$$i$$$ and column $$$j$$$ with an unordered edge of second type.
If state of $$$i$$$ is already set, $$$i$$$ and $$$j$$$ are connected with an edge than we can determine state of $$$j$$$. Lets iterate over rows $$$1, 2, ..., n / 2$$$ and columns $$$1, 2, ..., m / 2$$$. If current row's/column's state is already determined than lets throw a DFS from current row/column, setting other rows/columns that DFS gets to. If current row's/column's state is not determined than lets try both options. Set its state to true, send a DFS. Then set its state to false, send a DFS. Choose option with less reverse operations.











That's great, thanks.
Note: It's similar to C from here.
Special case: $$$l=r$$$
Getting the # of vertices that are at most a distance $$$k$$$ away from a fixed vertex is a well-known problem. It can be done with centroid decomposition and a table that stores prefix sums at each level of the decomposition.
General case:
For each query, consider the centroid $$$c$$$ of the tree and the computer $$$i$$$ that determines its infection time (namely, the $$$l\le i\le r$$$ which maximizes $$$t_i+dist(c,v_i)$$$). This can be computed with a segment tree.
Then the latest infection times for all computers $$$d$$$ outside the subtree of $$$c$$$ corresponding to $$$v_i$$$ will satisfy $$$infect_d=infect_c+dist(c,d)$$$. The number of such vertices that are infected within time $$$t$$$ can be computed as in the special case. Then we can recursively deal with the vertices inside the subtree corresponding to $$$v_i$$$ by considering the centroid of this subtree, and so on. Note that viruses that originate outside the subtree corresponding to $$$v_i$$$ must still be considered; this is what $$$extra$$$ is for in my solution.
This can be done in $$$O(N\log N+Q\log^2N)$$$ if we process all updates before all queries.
Suppose that we fix $$$j$$$ and we want to find the number of pairs $$$(i,k)$$$ which work. For a fixed element $$$x$$$, let $$$pre[x]$$$ equal the maximum $$$J\le j$$$ such that $$$a_J=x$$$. Similarly, let $$$nex[x]$$$ equal the minimum $$$J>j$$$ such that $$$a_J=x$$$. Then $$$(i,k)$$$ is okay if for all $$$x$$$, either $$$i\le pre[x]$$$ and $$$nex[x]\le k$$$ or $$$pre[x]<i$$$ and $$$k<nex[x]$$$. (It might help to plot the points $$$(pre[x],nex[x])$$$ on graph paper and shade in the possible regions for $$$(i,k)$$$).
This is quite similar to this CF task, where you're asked to modify a sequence and count the number of indices $$$i$$$ such that $$$\min(a[1\ldots i])>\max(a[i+1\ldots n])$$$ after every modification. Use a lazy segment tree that computes the minimum as well as the number of minimums, and supports addition updates on a range. The operations required for this problem are slightly more complex than those needed for that task (see the code for details).
Start with all the pairs $$$(pre[x],nex[x])$$$ for $$$j=1$$$. For each $$$j$$$ in increasing order, add the number of pairs $$$(i,k)$$$ which work for that $$$j$$$ to the answer. Then when you increase $$$j$$$ by one, only one of the pairs $$$(pre[x],nex[x])$$$ changes (which corresponds to a constant number of updates to the segment tree).
The functions "ad" and "del" correspond to adding and deleting a pair $$$(pre[x],nex[x])$$$, respectively. The meanings of nex and pre in the code might not be exactly the same as what I mentioned above. The overall time complexity is $$$O(N\log N)$$$.
Is there any source to upsolve IZhO 2020?
You can do it in group ACM in Kazakhstan here is the link: https://codeforces.com/group/Uo1lq8ZyWf/contests
.
Benq why did you do the analysis for the tasks of the first day and did not do it for the remaining tasks of the second day. If you can do task day2 C do this please.