Hi guys.
I have a problem want to ask you guys.
Problem: Given a tree with n nodes, m segments in a tree with 2 endpoints. Find the maximum number of segments satisfy that not exist two segments with the edge intersect. (n < 1e3, m < 1e5);
My solution (WA passed 4/5) is: Sort m segments by the depth of their LCA. If two segments have the same LCA, if one of them have the endpoint equal to their LCA i choose it ,else i choose the one have shorter length. After sorted, i pick it one by one.
My sub For example:
n = 6, m = 4;
edges:
1 2
2 3
3 4
3 5
3 6
segments:
1 3
4 5
5 6
6 4
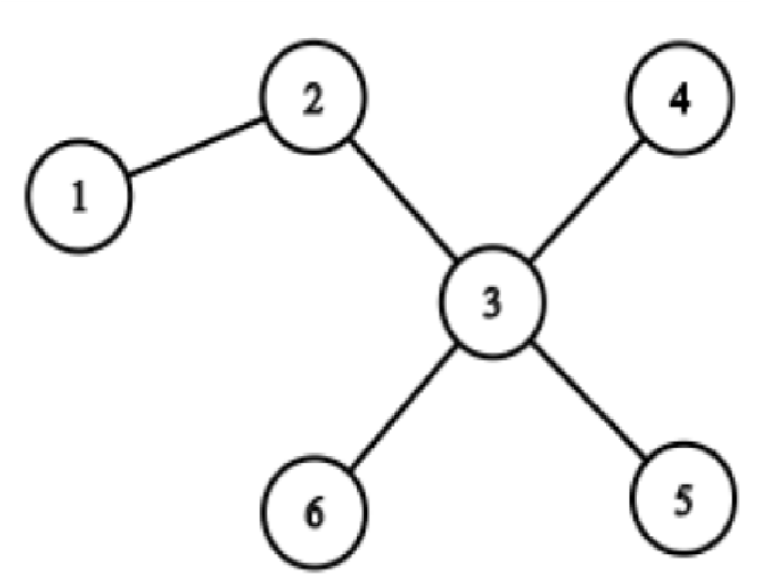
So the answer is 2 because we can choose segment (1, 3) and segment (4, 5) as path 1 -> 3 = 1 -> 2 -> 3, path 4 — > 5 = 4 — > 3 -> 5.
You also can choose (1, 3), (5, 6) or (1, 3), (6, 4)










Can you give link or something? Or at least explain better. Please don't expect people to understand what you mean by "Find the maximum number of segments satisfy that not exist two segments with the paths intersect."
Sorry for my bad english i will add an example to make it more clear
It is clear enough bro?
Ok, now I understand. Do you have any proof/intuition why your greedy algorithm should always produce the optimal solution? To me it is not at all clear why it should work — seems like unproven greedy.
My greedy algorithm is completely wrong. You have any ideas?
How about something like: let $$$\mathrm{dp}[u]$$$ be the most segments that can be fit completely in the subtree of $$$u$$$.
you miss one important detail that degree of each node is less than 10
do you have problem link?
No it's a problem given by my teacher