Problem A
At first let's notice that if there exists such triple ai, aj and ak that ai < aj < ak, then |ak - ai| > |aj - ai| and |ak - ai| > |ak - aj|.
Thus we can sort all numbers and check only adjacent ones. There are exactly n - 1 of such pairs. The only thing left is to find minimal distance of all pairs and count pairs with that distance.
Overall complexity: O(nlogn)
Problem B
The task was just about implementing algorithm described in statement.
This is one of many possible ways of doing this. Firstly you should notice that doing ai iterations in i-th step is equal to doing ai mod (n - i) iterations (0-based numbering). That is less than n.
Now fill array of length n with ones and create pointer to current leader. Then on i-th step move pointer to the right (from cell n - 1 proceed to 0) till you encounter ai mod (n - i) ones. When finished, write 0 to this cell and move pointer to next cell which contains 1.
Overall complexity: O(n2).
Problem C
Let's declare a function which takes number as a string and erases minimal number of digits in substring from 2-nd to last character to obtain beautiful number.
Note that if the answer for given string exists, then this function will erase no more than 2 digits. If the number is divisible by 3 then sum of its digits is also divisible by 3. So here are the only options for the function:
- Sum of digits is already equal to 0 modulo 3. Thus you don't have to erase any digits.
- There exists such a digit that equals sum modulo 3. Then you just have to erase this digit.
- All of the digits are neither divisible by 3, nor equal to sum modulo 3. So two of such digits will sum up to number, which equals sum modulo 3 ((2 + 2) mod 3 = 1, (1 + 1) mod 3 = 2). Let positions of non-zero numbers be a1, a2, ..., ak. Then you can easily see that its enough to check only three function outputs: on substrings [a1..n], [a2..n] и [a3..n]. We imply that all digits to the left of the taken non-zero digit are erased. As we can erase no more than 2 digits, these options will cover all the cases.
If there exists no answer for any of substrings, than you need to check if the number contains 0 — it will be answer in that case. If there is no 0, then answer is - 1.
Otherwise the answer is the function output of maximal length.
Overall complexity: O(n).
Problem D
In this editorial x represents the number of vertex we are currently in.
Let k be the maximum integer number such that x is divisible by 2k (or the number of zeroes at the end of the binary representation of x). It is easy to prove that if k = 0, then x is a leaf; if k = 1, then both children of x are leaves, and so on. Even more, the difference between x and any of his children is exactly 2k - 1. So to traverse to the left child, we have to subtract 2k - 1 from x (if x is not a leaf), and to traverse to the right child, we add 2k - 1 to x.
How can we process traversions up? Let y be the number of the parent node. y has exactly k + 1 zeroes at the end of its binary representation, so to traverse from y to x, we need to either add or subtract 2k from y. And to traverse from x to y we also have to either subtract or add 2k to x. One of these operations will lead us to the number divisible by 2k + 1 and not divisible by 2k + 2, and we need to choose this operation.
Time complexity is 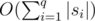
Problem E
f we want to divide all balls from some box into k sets with sizes x and x + 1 (and there are ai balls in this box), then either 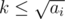 or
or  . So the solution will be like that:
. So the solution will be like that:
- Iterate over the possible sizes of sets x (from 1 to
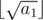 , or to some constant — in our solution it's 40000) and check if we can divide all balls into sets with sizes x and x + 1,
, or to some constant — in our solution it's 40000) and check if we can divide all balls into sets with sizes x and x + 1, - Then iterate over the number of sets k, calculate the sizes of sets if we want to divide the first box exactly into k sets and try to divide balls from all other boxes into sets of these sizes.
If we want to divide ai balls from the same box into k sets, then the sizes will be 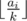 and
and 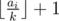 ; but if
; but if 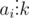 , then we also have to check if sizes can be
, then we also have to check if sizes can be 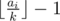 and
and 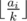 .
.
If we fix sizes x and x + 1 and we want to check whether we can divide a box with ai balls into sets with these sizes (and to get the minimum possible number of such sets), then the best option will be to take 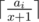 sets. If
sets. If 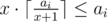 , then such division is possible. If not, then it's impossible to divide ai balls into sets of x and x + 1 balls.
, then such division is possible. If not, then it's impossible to divide ai balls into sets of x and x + 1 balls.
Time complexity of this solution is 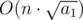 .
.
Problem F
Let's represent spells as points on cartesian plane. If we consider three spells A, B and C such that Ax ≤ Bx ≤ Cx and B is above AC on the cartesian plane or belongs to it, then we don't need to use spell B because we can replace it with a linear combination of spells A and C without any additional mana cost.
We can maintain the lower boundary of the convex hull of all points from 1-type queries and the point (0, 0). Then to process 2-type query we have to find the intersection of aforementioned lower boundary and the line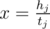 (our average damage in this fight has to be at least this value). If there is no intersection, then the answer is NO because even with infinite mana Vova's character can't deal that much damage before dying. If there is an intersection, we have to check that it is not higher than the line
(our average damage in this fight has to be at least this value). If there is no intersection, then the answer is NO because even with infinite mana Vova's character can't deal that much damage before dying. If there is an intersection, we have to check that it is not higher than the line 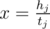 to ensure that we have enough mana to kill the monster in given time. Model solution uses only integral calculations, but it seems that long double precision is enough.
to ensure that we have enough mana to kill the monster in given time. Model solution uses only integral calculations, but it seems that long double precision is enough.
Time complexity: O(q·log q).









