Hi all,
Hope you are all safe with the unfortunate events occurring throughout the world.
I was solving some problems on HackerEarth's CodeArena platform (1v1 other person, 1 problem, 20 mins, who ever gets more TCs wins) , when I came across this problem (the contest has ended). I have attached the screenshot of the statement to this post.
I first attempted to use combinatorics and math to solve it, but later changed to applying DP. However, I couldn't figure out a recurrence between the states (# of objects, # of groups).
I would really appreciate it if someone could lend a helping hand with the recurrence. Also, IF there is an easy mathematical solution to the problem, please share it.
Thanks for your help and time! BC
EDIT: Sorry, I assumed that the 'Add Image' feature automatically appended the image to the post. Attached below is the image. 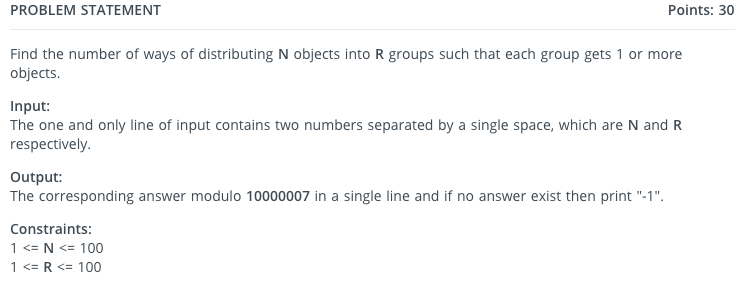
Sample TC: Input: 4 2
Output 3










DP[i][j] = #of ways to put 'i' objects given 'j' open groups.
You have 2 transitions:
Add the current object to an open group — DP[i + 1][j] += j * DP[i][j]
Create a new group — DP[i + 1][j + 1] += DP[i][j]
Answer is DP[N][R]
Wouldn't transition 2 be DP[i][j.+ 1] += DP[i][j]?
You do not add an object every time you create a group?
How can you have a group without an object?
I like to pretend this is some philosophical question. "But how can there be a group if there is no object"?
My username also poses an interesting philosophical question: "Is water wet?"
But, Mr. wet_water, adding an object isn't a necessary requirement for creating a group!
Can you read the problem again, it says that each group must have at least 1 person
I think this is a classic stars and bars problem, you can read an introduction of that here. https://cp-algorithms.com/combinatorics/stars_and_bars.html
The problem can be easily solved with a simple recursive DP that works in O(N*R). Here is the code: https://ideone.com/c0Hjq2
Explanation: First, lets fill all the DP array values' to -1. Start a recursive function that has two parameters x y for example. Let x be the index of N. Let y be the objects that are currently available. If y is less than 0, then there is no answer. So return 0.(We are building up in this type of DP). But if x reached n, and y is equal to 0, then the job is done and it successfully distributed all of its objects so it return 1. Otherwise, if x reached n and y isn't equal to 0, then it didn't finish its objects so it returns 0. We will run a for loop from 1 to y and try and distribute 1 object to the current group we are one, 2 objects to the current group we are on, 3,4,... until y. We will subtract what was taken from the objects and run that recursive.
Edit: Found a combination solution which is: (N-1)C(R-1)(C means combination) But notice that: You cannot divide a number with modulo. You can read more about it: Here
dp[i][j]->total number of ways to group i numbers of objects in j number of groups.
There are two possibilities either we create a new group or don't create a new group so the recurrence relation will look like this....
dp[i][j]=dp[i-1][j-1]+j*dp[i-1][j]
it is simply (n-1)C(r-1).
The question is a bit vague. When are two ways considered different? Are the groups differentiable. If yes then the solution is the coefficient of x^n in (x+x^2+x^3+...+x^n)*(x+x^2+x^3+...+x^n)*... r times (since there are r groups and we have to distribute total n items, also the power of x starts from 1 because we have to select atleast 1 item for a group). So,
coefficient of x^n in (x+x^2+x^3+...+x^n)*(x+x^2+x^3+...+x^n)*... r times
=>coefficient of x^n in x^r*(1++x+x^2+x^3+...+x^(n-1))*(1+x+x^2+x^3+...+x^(n-1))*... r times
=>coefficient of x^(n-r) in (1+x+x^2+x^3+...+x^(n-1))*(1+x+x^2+x^3+...+x^(n-1))*... r times
=>coefficient of x^(n-r) in (1-x)^(-1)*(1-x)^(-1)*... r times
=>coefficient of x^(n-r) in (1-x)^(-r)
=>(r+n-r-1)C(n-r)
=>(n-1)C(n-r)
=>(n-1)C(r-1) (since nCr = nC(n-r))
This can also be solved using dp. The state is dp[i][g], where dp[i][g] is the solution for the subproblem items [i:n-1] with g groups remaining. So the final solution is dp[0][r] or solve(0, r). A recursive method would look like: