Introduction
The link-cut tree data structure represents a rooted forest (a collection of rooted trees) and can perform the following operations in $$$O(\log n)$$$ amortized time (here, a node represents a vertex of the tree):
link(par, child): Attach a tree (child) as a child of another tree's node (par).cut(node): Detach node's subtree from node's parent.find_root(node): Find the root of a node.lca(u, v): Find the least-common ancestor of two nodes.
Structure:
The represented forest (which is represented by the link-cut tree) is split into disjoint, vertical preferred paths composed of preferred edges linking each node with the latest child on the access path. On each preferred path we store a splay tree, sorted by increasing depth. You'll want to know splay trees for link-cut trees so see my splay tree tutorial for a tutorial on splay trees, which are a type of balanced binary search tree. Each preferred path has a path-parent pointer pointing to the root of the parent preferred path (if it exists). So, each edge is either a preferred path edge or path-parent edge.
Diagram:
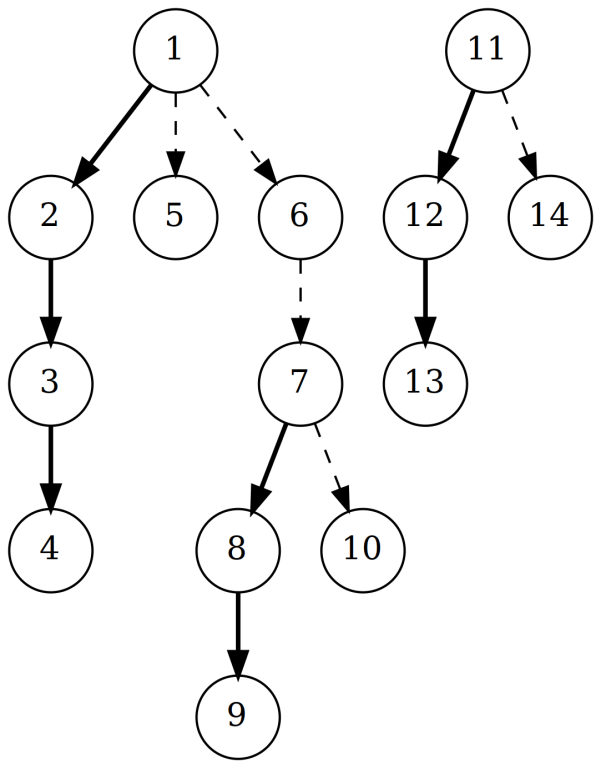
Here, bold edges denote preferred path edges and dashed edges denote path-parent edges. 1 and 11 are the roots of the two trees in the represented forest. The preferred paths are (1,2,3,4), (5), (6), (7, 8, 9), (10), (11, 12, 13), (14).
Avoiding confusion:
Be careful to distinguish the splay tree (the implementation detail) from the represented forest (what we actually care about as a user). Note that the path-parent pointer is different from the splay tree parent pointer. Also note that the root of a tree in the represented forest may not be the splay tree root of the splay tree containing it. Likewise, the splay tree children do not correspond to represented forest children.
Implementation:
Splay tree
Each node will store an additional path parent pointer. Note that since exactly one of the path parent or splay tree parent pointers are null, we can actually store the path-parent pointer in the parent pointer. However, here we choose not to do so, for the sake of simplicity.
The splay tree code must be modified so that the path parent pointer is set to the splay tree parent's path parent pointer.
Splay tree code:
/** @brief Implements a splay tree*/
template<typename T>
struct SplayNode{
SplayNode(){}
SplayNode(T value_arg): value{value_arg} {}
T value{}; //!< Value associated with node
array<SplayNode *, 2> child{}; //!< Left and right children
SplayNode *parent{}; //!< Pointer to parent
Node* path_parent{}; // Added for link-cut tree
bool side() const {
/*! Returns true if child is on the right, and false otherwise*/
return parent->child[1] == &this;
}
void rotate() {
/*! Rotate node x around its parent */
const auto p = parent;
const bool i = side();
if (p->parent) {
p->parent->attach(p->side(), &this);
} else {
parent = nullptr;
}
p->attach(i, child[!i]);
attach(!i, p);
this.path_parent = p->path_parent; // Added for link-cut tree
}
void splay() {
/*! Splay node x. x will become the root of the tree*/
for(;parent;rotate()) {
if (parent->parent) {
(side() == parent->side() ? parent: &this)->rotate();
}
}
}
array<SplayNode *, 2> split() {
splay();
// TODO use detach function
const auto right = child[1];
if (right) {
right->parent = nullptr;
}
this->right = nullptr;
return {&this, right};
}
void attach(bool side, SplayNode *const new_) {
/*! Attach node new_ as the node's side children*/
if (new_) {
new_->parent = &this;
}
child[side] = new_;
}
};
Access
The key operation we need is the access(node) operation which moves the node to the root of the splay tree containing the root of the tree containing node in the represented forest. Note that this does not affect the represented forest, but merely reorganizes the internal splay trees and preferred paths. To implement access(node), we splay the node and convert the node's path-parent edge into a splay tree edge (effectively merging the two preferred paths and their splay trees). For implementing access, we use a helper function detach_child which converts a preferred child edge to a path parent edge, effectively splitting the preferred path.
Now we can implement all the other operations in terms of access.
Node *make_tree() {
/*! Make a new tree */
return new Node{};
}
void detach_child(Node* node){
/*! Converts node's preferred child edge to a path parent edge*/
if(node->child[1]){
node->child[1]->path_parent = node;
node->child[1]->parent = nullptr;
}
}
Node *access(Node *node) {
/*! Moves node to the root of the auxillary tree containing the root node of the tree. Returns last path-parent of node as it moves up the tree*/
node->splay();
detach_child(node);
node->child[1] = nullptr;
Node *par = node;
while (node->path_parent) {
par = node->path_parent;
par->splay();
detach_child(par);
par->attach(1, node);
node->path_parent = nullptr;
node->splay();
}
return par;
}
Find root
For find_root(node), we call access(node), and then we find the node with minimum depth in the splay tree containing the (represented forest) root by repeatedly walking to the left child. Since this node has minimum depth, it must be the root. So now node equals the (represented forest) root node. We then access(node) which splays the root to speed up future find_root calls.
Node *find_root(Node *node) {
/** Finds the root of the tree containing node*/
access(node);
for (; node->child[0]; node = node->child[0]);
access(node);
return node;
}
Cut
For cut, we access the node and then detach it from it's splay tree left child, which is its parent in the represented forest.
void cut(Node *node) {
/*! Detaches the subtree of node from the tree of node's parent*/
access(node);
node->child[0]->parent = nullptr;
node->child[0] = nullptr;
}
Link
For link(parent, child), we access the child and then access the parent. Then we simply attach the parent as the child's left (splay tree) child.
void link(Node *par, Node *child) {
/*! Makes child the child of par*/
access(child);
access(par);
child->attach(0, par);
}
For finding the LCA, we access u, then return the last path-parent of the node (before it becomes the root of the splay tree containing the represent tree's root). This last path-parent node is the node separating the subtree containing u from the subtree containing v.
Node *lca(Node *u, Node *v) {
/*! Returns lowest common ancestor of nodes u and v or nullptr if u and v are in different trees*/
if (find_root(u) != find_root(v)) {
return nullptr;
}
access(u);
return access(v);
}
Obligatory shill comment: my C++ template library OmniTemplate has code for link-cut tree and splay tree (and more).
Uses:
This data structure can be used to speed up Dinic's algorithm from $$$O(V^2 E)$$$ to $$$O(EV\log V)$$$.
You can also augment this with path sums (and other monoid operations) by augmenting the splay tree with sums stored in each node. You can alternatively augment it with subtree sums/size by storing the sum of subtree generated by only considering the path-parent edges in each node and then updating it while performing operations.
Link-cut tree problems:
Use this link-cut tree testing problem to test your link-cut tree implementation.
Train tracks. Credit: Monogon










