Introduction
This tutorial is about ear decomposition, a simple but powerful technique for finding graph connectivity, including 2-vertex-connectivity, 2-edge-connectivity, and strong orientation.
In this tutorial we assume we have a connected graph. If the graph is disconnected, the algorithm can be run on each connected component.
An ear consists of a path where the endpoints (the first and last vertices) could be the same or different. So a cycle can be an ear. (It is called an "ear" because it is shaped like the human ear.)
An ear decomposition1 is a decomposition of a graph into a sequence of ears $$$C_1, C_2, \dots, C_n$$$. $$$C_1$$$ must be a cycle and each later ear must be either a path between two vertices that are on previous ears, or a cycle with one vertex on a previous ear.
Since every edge in an ear belongs to a cycle, an ear decomposition has no bridges. So, a connected graph is 2-edge-connected iff it has an ear decomposition containing all its edges.
In an open ear decomposition all ears except the first are paths. A connected graph is 2-vertex-connected iff it has an open ear decomposition containing all its edges. Note that 2-vertex-connectivity implies 2-edge-connectivity.
Finding ear decomposition
To find an ear decomposition, we use the algorithm in Schmidt (2013b)2. Run a DFS on the graph. Root each edge in the DFS tree towards the root and each backedge away from the root. Note that each edge in a DFS tree is either a backedge between a vertex and its ancestor or a tree edge. For each vertex in DFS order, we loop through each backedge, and traverse the unique directed cycle containing the backedge until we hit a previously visited vertex. The path we traverse is the ear. Note that the first and last vertices of each ear apart from the first one are previously visited. So, if every edge is contained in a ear, we have an ear decomposition of the entire graph, otherwise we have an ear decomposition for a subgraph. The time complexity of this approach is $$$\Theta(|E|+|V|)$$$ since we visit each edge and vertex once.
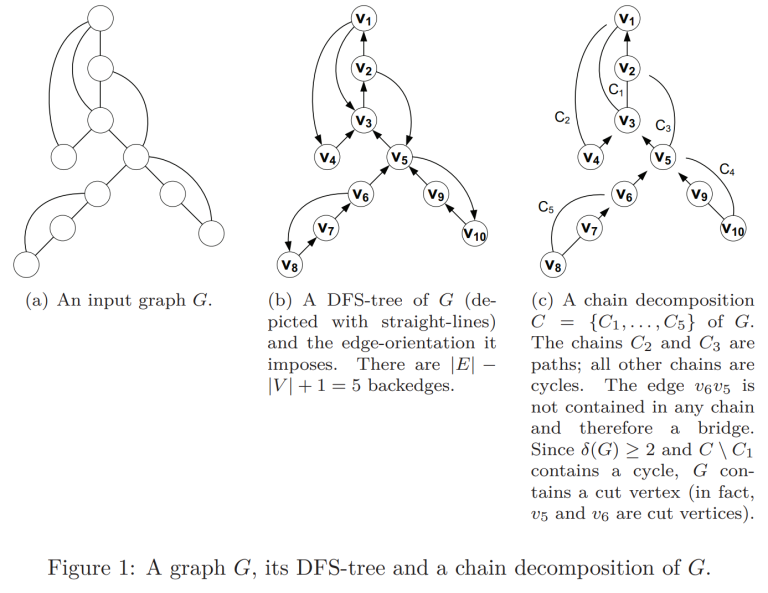
Source: 2
Finding bridges
A bridge is an edge of the graph whose removal splits the graph into multiple connected components.
The bridges of the graph are exactly the edges that are not in any ear, because the ear decomposition consists of all the edges which are part of a cycle.
Finding articulation points
Analogously, an articulation point is a point of the graph whose removal splits the graph into multiple connected components.
The articulation points are exactly the vertices which are on the endpoint of a cycle apart from $$$C_1$$$ or a bridge.
Strong orientation
A graph has a strong orientation iff the graph has an ear decomposition containing all its edges. To find the strong orientation, we simply orient the graph based on the DFS as described above.
Code:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
/*! \brief Returns an open ear decomposition of the graph.
* \returns A list of ears for each connected component of the graph is returned.*/
auto ear_decomp(const vector<vector<ll>> &graph) {
vector<ll> ear_visited(graph.size()), dfs_visited(graph.size()), parent(graph.size());
vector<vector<vector<ll>>> ears_list;
for(ll root = 0; root < graph.size(); ++root) {
if (dfs_visited[root]) {
continue;
}
// Perform a DFS
vector<ll> queue;
const auto dfs = [&](const auto& dfs, ll u) -> void {
dfs_visited[u] = true;
queue.push_back(u);
for(const auto v: graph[u]){
if(dfs_visited[v]){continue;}
parent[v] = u;
dfs(dfs, v);
}
};
dfs(dfs, root);
vector<vector<ll>> ears;
for (const auto u : queue) {
for (const auto v : graph[u]) {
if (parent[u] == v || parent[v] == u) {
continue;
}
// Found a backedge. Now traverse the ear.
vector<ll> ear{u};
ear_visited[u] = true;
for(ll x = v; ; x = parent[x]){
ear.push_back(x);
if (ear_visited[x]) {
break;
}
ear_visited[x] = true;
}
ears.push_back(ear);
}
}
ears_list.push_back(ears);
}
return ears_list;
}
/*! @brief Finds biconnected components of graph using ear decompositions.*/
auto biconnected_ear(const vector<vector<ll>>& graph) {
// art_points[i] = whether vertex i is an articulation point
vector<ll> art_points(graph.size());
// Bridge edges
vector<array<ll, 2>> bridges;
// Find ears apart from the first one which are cycles.
const auto ear_list = ear_decomp(graph);
for (const auto &ears : ear_list) {
for(ll i = 0; i < ears.size(); ++i) {
if (i != 0 && ears[i].front() == ears[i].back()) {
art_points[ears[i].front()] = 1;
}
}
}
// Graph containing all ear edges
vector<vector<ll>> ear_graph(graph.size());
for (const auto &ears : ear_list) {
for (const auto &ear : ears) {
for(ll i = 0; i < ear.size() - 1; ++i) {
const auto a = ear[i], b = ear[i+1];
ear_graph[a].push_back(b);
ear_graph[b].push_back(a);
}
}
}
// Find edges which are not in ear decomposition
vector<ll> ear_adj(graph.size());
for(ll u = 0; u < graph.size(); ++u) {
vector<ll> non_ear_adj;
const auto set = [&](const bool val){
for(const auto v: ear_graph[u]){
ear_adj[v] = val;
}
};
set(true);
for(const auto v: graph[u]){
if(!ear_adj[v]){
non_ear_adj.push_back(v);
}
}
// Clear ear_adj efficiently
set(false);
for (const auto x : non_ear_adj) {
if (u < x) {
array<ll, 2> edge{u, x};
bridges.push_back(edge);
for(const auto v: edge){
if (graph[v].size() > 1) {
art_points[v] = true;
}
}
}
}
}
return {art_points, bridges};
};











It seems like the code above have some bugs.
The input is a $$$C_4$$$, but the code considers [3, 0] as a ear. When checking backedge, we should take the depth of u and v into consider in case that same edge being used twice (which happened in the input above.)
Also, the
biconnected_earfunction have an error for returning initalizer list under C++17 compiler.