320A - Magic Numbers
Although the input number is very small, solving the problem for arbitrary length numbers using strings is easier. It's easy to prove that a number meeting the following conditions is magical:
- The number should only consist of digits 1 and 4.
- The number should begin with digit 1.
- The number should not contain three consecutive fours (i.e. 444).
Here is a sample implementation in C++:
#include <iostream>
#include <string>
using namespace std;
bool is_magical(string number) {
for (int i = 0; i < (int)number.size(); i++)
if (number[i] != '1' && number[i] != '4')
return false;
if (number[0] == '4')
return false;
if (number.find("444") != number.npos)
return false;
return true;
}
int main() {
string number;
cin >> number;
if (is_magical(number))
cout << "YES" << endl;
else
cout << "NO" << endl;
return 0;
}
320B - Ping-Pong (Easy Version)
Imagine the intervals as nodes of a graph and draw directed edges between them as defined in the statement. Now answering the second query would be trivial if you are familiar with graph traversal algorithms like DFS or BFS or even Floyd-Warshall!
Here's an implementation using DFS: 3951145
And here's an implementation using BFS: 3947426
Finally an implementation using Floyd-Warshall: 3945330
319A - Malek Dance Club
Solving this problem was easy when you modeled the assignment with two sets of points numbered from 0 to 2n - 1 (inclusive) paired with 2n line segments. Each line segment corresponds to a dance pair. And each pair of intersecting lines increase the complexity by one.
Imagine you now the solution for binary string x. Now we want to calculate the answer for 1x and 0x easily. Look at the figure below:
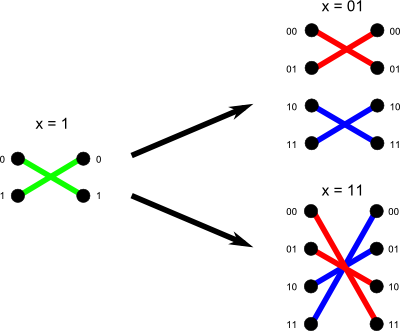
The figure shows what happens in a simple case. Whenever you append 0 before x the same structure appears twice in the result. But whenever you append 1 before x the same structure appears twice but the first half of points in right column are swapped with the second half. This increases the number of intersections by size of first half times size of the second half.
So if x has length n and f(x) is the complexity of the assignment then we have:
- f(0x) = 2f(x)
- f(1x) = 2f(x) + 22n
An interesting fact is that f(x) is equal to x2n - 1.
319B - Psychos in a Line
Will be fixed :)
Let's find the murderer! Well, if you look close you see that each psycho is murdered by the nearest psycho on his left which has a greater id.
Now let ti be the number of the step which i-th psycho in the line is murdered (not the psycho with id equal to i). Assume j-th psycho in the line be the nearest psycho with a larger id than i-th psycho in the line in his left. As we know j-th psycho kills the i-th psycho. We also now that this happens when all psychos between j and i have been killed. So ti = max(tj + 1, ..., ti - 1) + 1.
Now we have a simple O(n2) solution using the above observations. To make things run faster you should be familiar with a classic problem. This problem asks to find the nearest greater element to the left of each element in a array. This problem has a O(n) solution. You can solve it yourself or read about it here.
After knowing about all these things it wouldn't be hard to figure out a way to solve this problem efficiently. Here is a cute implementation of what is described above: 3945963
319C - Kalila and Dimna in the Logging Industry
This problem is equal to finding the minimum cost to cut the last tree completely. Because any cutting operation can be done with no cost afterward. Let dpi be the minimum cost to cut the i-th tree completely. It's easy to figure out that we can calculate dpi if we know the index of the last tree which has been cut completely (j-th tree). Knowing this dpi would be equal to dpj + bjai. So dpi = minj = 1..i - 1(dpj + bjai).
Using the above information the problem has an easy dynamic programming solution in O(n2). There's a known method which can be used to improve recursive relations with similar form. It's called Convex Hull Trick. You can read about it here.
319D - Have You Ever Heard About the Word?
TODO
319E - Ping-Pong
TODO











Always the most interesting problems is coming soon!
Well, that's because I'm tired right now. I hope I don't get lazy and do the rest of the editorial in the morning! :D
Well , I meant maybe the editorialist should start writing the solution of hardest problems first then if he/she got tired or something happened prevented her/him from continuing writing the editorial then the easiest problems will be coming soon ..
Any updates on the TODO.
Tomorrow never does
bro, just wait until tomorrow
tomorrow I guess.
tomorrow...
http://www.shuizilong.com/house/archives/codeforces-round-189/ (Solution for problem E. Chinese ...
" Well, if you look close you see that each psycho is murdered by the nearest psycho on his left which has a greater id" are u sure this statement is correct? (10 9 1 2 3 4 5 6 7 8, 8 is killed by 10, not 9) Anyway it doesn't affect the following solution.
I had the idea of the solution in my mind. Looks like I've made a mistake, Since I haven't done the preparation of this problem.
I'll fix it tomorrow, thanks for mentioning.
Hope it will be fixed soon, thanks.
I hope you can manage to fix it soon. Thanks:)
havaliza , tutorial is coming or not
LOL, he found his problem so hard that he couldn't update the tutorial for 7 years
havaliza. it is now 7 years of the tutorial. tomorrow never comes. :)
I think the solution goes more like this. A given psycho X will be killed only when all elements for which X is the first greater element to the right from them is killed. And the life time of X will max of life times of those elements plus one. So the algorithm does the linear solution for finding next greater element for each element while tracking also the life times as items are popped off the stack.
Yes you are right, each psycho X is murdered by the nearest psycho on his left which has a greater id Y, Unless Y is itself not murdered by another psycho Z, which will take its place , but it won't take affect the solution since in that case Y will be killed by Z before it reaches X or else Y will kill X itself.
for Problem C (div 2) or Problem A (div 1) here is a much better solution. We have to find number of pairs (a,b) & (c,d) such that a < c and b > d. Obviously if a < c then we can assume in binary a is of the form A0B and c is of the form A1C where 'A' is the starting set of bits that are same in both. For example, if a= 111010 and c= 111111 then here A= 111, B=10 and C= 11. Now when we perform b= a xor x and d= c xor x then A would get converted to a new set of bits (say D) which is same in both case. Now in order to make b>d we should have 1 in x in a position of 0 after A in a which would convert 0 in a to 1 and 1 in c to 0 making b>d. So let us have a binary string x. For each i (1-based) such that x[i]='1' we can have pow(2,i-1) possibilities for A, pow(2,n-i) possibilities for B and pow(2,n-i) possibilities for C.
vary good explaination , i didnot get the editorial's solution but your explaination is perfect and easily understandable
We are looking forward to D-E problems editorial.
Problem D: Seems that brute force works here if done well. The complexity is quadratic, but the constant is (I think) around 3/8. Since the operations you are doing are fairly simple and linear (which is good for caching), that seems to be good enough. I'm pretty sure the worst case for this solution is where you actually don't have any changes in the string so it's easy to test for timeout.
I've seen a few solutions that use hashing to test if it's possible that there will be a pair of a certain length and only then try to actually find it. For this kind of solution, the worst case seems to be one where there are a lot of changes (perhaps one per size to minimize the string length reduction) because you need to recompute the hashes when a change happens. On the other hand, it's blazingly fast when there are no changes. Since changes reduce the size of the string, I think you can only have about sqrt(N) different length pairs.
Problem E: The key thing to think about in this problem is what do we get from the restriction that the interval length is strictly increasing. There are two ways that two intervals can interleave. First, they can be interleaved in a way such that one endpoint of both intervals is inside the other interval which leads to a bidirectional "road" between the intervals. The other way is that one interval can be completely contained inside another which leads to a unidirectional road.
Now, if we are adding a new interval (a, b) and find an interval (c, d) that contains one of the endpoints a or b, then we know that there will be a bidirectional road between these two intervals, and this is a consequence of the requirement that interval lengths increase over time.
So the idea is this. We will use a union-find data structure to store strongly connected components of intervals (i.e. sets of intervals where there will be a path between any two of them). To answer a query, we find the components of intervals a and b. If they are in the same component, the answer is obviously "YES". Otherwise, it might still be that the component containing b completely engulfs the component containing a (and therefore a itself) which also implies there is a path from a to b, i.e. the answer is "YES". Otherwise, the answer is "NO".
What remains is to maintain and update these components. For this, we will use a tournament tree. A frequent "trick" that makes it possible to use a tournament tree when the value range in question seems to be really large (here it is -10^9 to 10^9) is to remap these values to a much smaller range that is determined by the number of values that we get. Here, there are at most 10^5 intervals, so at most different 2*10^5 values. See the code for details.
So, in the node of the tournament tree that represents the segment [a, b>, we store a set of component indices that completely cover this segment. Then when adding a new interval (query type 1), we use the increasing length property: we first "query" the tournament tree with the left endpoint and then with the right endpoint. Whenever an endpoint is contained inside some previously computed component, we join the previously computed component with the component containing our new interval. When joining components, we update L[x] and R[x] to contain the leftmost endpoint of an interval in component x and the rightmost endpoint of an interval in component x, respectively. On more important thing is that we need to remove all old components from a tournament tree node when we join components because we only want to have one instance of a component in the set (only the "leader" from the union-find data structure) and all the components in a certain node will get joined with our new interval. We finally add this new component back into the tournament tree.
Anyway, sorry for the imperfect explanation, but if you have any questions, I'll try to reply.
.
I would be more than happy if you tell me whether my thoughts about 319D - Have You Ever Heard About the Word? were right or not.
Here is my blog entry: http://codeforces.com/blog/entry/8150
Thank you.
In 319C — Kalila and Dimna in the Logging Industry, how can one prove that the answer fits in a 64 bit int? Can't we have a solution where we have to cut trees in order i=0,1...n and the values are similar to - a[1]=10^9-n, a[i]=a[i-1]+1 if i>1 - b[0]=10^9,b[i]=b[i-1]-1 if i<n-1 - n=10^5.
Realized that there is always the option of cutting tree a[i] directly after cutting the first tree. Hence, the answer will never exceed 10^14 (= 10^5 * 10^9) . Silly me.
The answer may exceed 10^14, for a case like,
But we can prove that the answer won't exceed 10^18 because in the extreme case, b[0] = 1e9 and a[n] = 1e9 and in that case it's sufficient to cut the n th tree to the ground right after the first one. So it is proved that the result will always <= 1e18 :-)
Regarding 319B, my solution goes like this:
First, let's try a O(N^2) approach. Because why not :D We process psychos from left to right, and remember psychos that live before turn k in an array T[k] (so T is a 2D array; it's sufficient to only consider 0 <= k <= N). The leftmost one always lives. Now when adding the next psycho, we go from turn 0 to turn N and if the rightmost psycho that lives before turn i has larger id, then this added psycho dies at turn i+1, so we append him to the ends of T[0 <= k <= i] (or to T[0 <= k <= N], if he never dies). The answer is maximum of all i+1 of dying psychos (or 0 if the sequence is decreasing). This is just a bruteforce, but it's constructed positionwise and not timewise.
It's actually easier to optimize this approach to O(N).
First, observe that we're only interested in the last element of every T[k]. So we make T[k] an integer and we assign to this variable instead of appending to an array.
Next, we remember just intervals of equal values in T[], on a stack — for each interval, we remember the value and its right end (the left end is given implicitly by the previous one), and as they'd go from left to right, we remember them top to bottom.
Now, we do the same thing as in bruteforce, but go over entire intervals of equal values of T[] in 1 step, instead of going over separate values. The trick to time complexity is here: each of N intervals is added at most once, and if we replace all values in it by a new interval, we delete it also at most once, so the total time is O(N).
Implementation: 4050295
Heyi havaliza , can you please fix the tutorial for the Psychos in a Line problem ?
What's wrong with it in the first place and why is it striked out?
I'll take the liberty to write some comments about these problems that aren't covered in the editorial.
First Problem B (Psychos): I have 2 solutions for this one. The simpler one to code and explain is this. The idea is as follows. You want to compute for each psycho the "time" (i.e. turn) in which it gets killed (I call this tdeath[i] in the code). The solution is then the max of all these times plus 1. The key observation is that tdeath[i] cannot depend on anything that happens to the right of the psycho, i.e. it is completely determined by what happens on its left.
So, how is it determined by what happens on the left? If there's a taller psycho directly to your left, you will die right away (in turn 0). However, if there is a shorter psycho directly to your left, you can't possibly die before he does. Now, if he gets killed by a psycho that is taller than you, that psycho will also kill you in the very next turn. Otherwise, if the psycho just left of you gets killed by a psycho that is still shorter than you, you have to wait for that psycho to get killed before you die. This can go on for some time before ultimately a taller psycho comes along and kills you. The idea is to store this sequence of "active" psychos on a stack and process the whole line from left to right.
It turns out it is convenient to set tdeath of psychos that don't ever die to -1. The first psycho has tdeath = -1, and we put him on the stack. Now for the ith psycho, we look at the top of the stack. If the psycho on the stack is shorter than the ith psycho, we update the ith tdeath and pop the stack. We can pop the stack because the psycho on the top of the stack will not kill any psychos to the right of the ith one. Furthermore, if we emptied the stack by this procedure, that means that the ith psycho is the tallest psycho in this prefix of the line so it never dies (set tdeath to -1).
Since any psycho can be pushed and popped to/from the stack at most once, the time complexity is O(N).
The second solution that I thought of first but is a bit harder to code is the following. We use a tournament tree to find the tallest psycho in some interval. We represent the line with a random-access doubly linked list and we simulate the process. The code is here. So, in the tournament tree, M is the maximal height in the interval represented by a node and P is the original position of the tallest psycho in that interval that isn't already dead. The change function does one iteration of the process. First, you find the tallest psycho and remove the decreasing subsequence to its right. You recurse on the left of the tallest psycho and on the part after the decreasing subsequence. The key optimization that makes this run in time is that if there is no change in some interval at any point in time, there can't be any change later on either (that's what the line T.kill(l, r) does).
I'm not completely sure what the worst case for this algorithm is. When there is a change in every tried interval, there will be at most around logN rounds so the run time will be about O(NlogNlogN). If there are no changes in some intervals, then that part of the line will be skipped in all further rounds. If anyone can come up with a case to fail this solution or to describe the worst case, I'd be grateful for the reply :)
What is tournament tree ? i think same thing is possible with segment tree !!
BTW, thanks for the explanation. :)
It's probably the same thing. I've heard tournament trees called "segment trees" and "interval trees" (though there's a different data structure called "interval tree" that stores a dynamic set of intervals and answers the query "is there an interval intersecting [a, b] in the set" in logarithmic time).
If you look at wikipedia's definition of a "segment tree" (http://en.wikipedia.org/wiki/Segment_tree), you'll see that it's more in in line with what I've described above for an interval tree.
I like the name "tournament tree" because if you draw this tree, it actually looks like a 2^n players single elimination tournament bracket (i.e. it's a complete binary tree).
can anyone explain how to use convex hull trick in 319c, i want to exactly know about the fact that how to convert this question into y=kx+b lines question sorry for very bad english ...
probably you should learn convex hull better, then the solution will be obvious for u
dp[i]=min(dp[j]+b[j]*a[i]) for all j<i here m=b[j] and b the intercept=dp[j] and a[i] is out x.
See THIS you will get more idea.
You're too lazy to write the editorial for a problem? Just write TODO and problem solved ;)
https://codeforces.com/problemset/problem/319/C
I did not understand the problem C clearly. Please anyone explain what we have to do elaborately?
Thank you.
For the Editorial for Problem A : I didnot understand the condition :
What is the logic of checking under && condition.??Can somebody please explain this?Thanks
It is checking , if any digit in the input is neither 1 nor 4, then straight away, saying, that the answer is "NO". Because in the question it is mentioned, that the number Shou only consist of digits 1 & 4.
Thanks for the clarification.Can we use statement in or like if(s[i] != '1' || s[i] != '4') meaning if we have either not 1 or not '4' then return false.?
No... Bro.. because that way this if condition will become true for every digit. See lets say digit is '1'. if(s[i] != '1' || s[i] != '4') return false;
if( false || true) So overall condition becomes true. And it returns false. It is not correct.
The and condition is important... Because we can return false only when a digit is not '1' AND at the same time it is also not '4'.
Can someone please explain why I am getting MLE in 319B - Psychos in a Line for this solution? Code- 83289131
void val(vector a, int &count)
When you pass a vector to a function, the entire contents is copied to a new vector and the old one stays in memory, so your old ones aren't getting cleared and you are using too much memory by saving them. You can pass by reference, but it seems that that won't make your code pass. Simulating the operations gives TLE (I tried it). Therefore try to improve your algorithm.
Thanks for your help.I get it now
You are so pigeon
I'm still waiting for 319B havaliza
IN 320B
why this is not working 145740758
As far as I consider, this should be a directed graph. For instance, for two intervals a=[2,5] and b=[1,6], we could reach b from a, but can not reach a from b. For your codes where you deal with "j and k", I think it is not correct to "push_back" both "directions". Maybe you could have a look at my solution (although it has been a long time ago).
Idk why 319B is crossed out, and no one mentioned this approach so here is my solution:
Just simulate each turn. It's clear that if we can process one death in $$$O(1)$$$ then the solution would be $$$O(n)$$$, since there are at most $$$n - 1$$$ death.
If we store the psycho in a linked list, then we can easily find out who will be death in the next turn by just checking whenever 2 elements become adjacent. One simple way to process multiple death in one turn is just to process them from right to left, you can see my implementation here: 179449591.
I think this approach was overlooked because linked-list are often neglected by CPers.
319B)
My approach
For the next iteration
Efficiently iterating only through indices where recent changes were made.
https://codeforces.com/contest/319/submission/187921145
A hack of 319E:
Input: 5 1 1 3 1 2 5 1 1 5 2 1 3 2 3 1 Output: YES NO
You will be wrong in this case if you judge two different segments after merge which have same value incorrectly.
Bump for editorial