Several recent problems on Codeforces concerned dynamic programming optimization techniques.
The following table summarizes methods known to me.
| Name | Original Recurrence | Sufficient Condition of Applicability | Original Complexity | Optimized Complexity | Links |
|---|---|---|---|---|---|
| Convex Hull Optimization1 |  | b[j] ≥ b[j + 1] | O(n2) | O(n) | 1 2 3 p1 |
| Convex Hull Optimization2 | dp[i][j] = mink < j{dp[i - 1][k] + b[k] * a[j]} | b[k] ≥ b[k + 1] | O(kn2) | O(kn) | 1 p1 p2 |
| Divide and Conquer Optimization | dp[i][j] = mink < j{dp[i - 1][k] + C[k][j]} | A[i][j] ≤ A[i][j + 1] | O(kn2) | O(knlogn) | 1 p1 |
| Knuth Optimization | dp[i][j] = mini < k < j{dp[i][k] + dp[k][j]} + C[i][j] | A[i, j - 1] ≤ A[i, j] ≤ A[i + 1, j] | O(n3) | O(n2) | 1 2 p1 |
Notes:
- A[i][j] — the smallest k that gives optimal answer, for example in dp[i][j] = dp[i - 1][k] + C[k][j]
- C[i][j] — some given cost function
- We can generalize a bit in the following way: dp[i] = minj < i{F[j] + b[j] * a[i]}, where F[j] is computed from dp[j] in constant time.
- It looks like Convex Hull Optimization2 is a special case of Divide and Conquer Optimization.
- It is claimed (in the references) that Knuth Optimization is applicable if C[i][j] satisfies the following 2 conditions:
- quadrangle inequality:
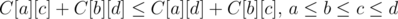
- monotonicity:

- It is claimed (in the references) that the recurrence dp[j] = mini < j{dp[i] + C[i][j]} can be solved in O(nlogn) (and even O(n)) if C[i][j] satisfies quadrangle inequality. YuukaKazami described how to solve some case of this problem.
Open questions:
- Are there any other optimization techniques?
- What is the sufficient condition of applying Divide and Conquer Optimization in terms of function C[i][j]? Answered
References:
- "Efficient dynamic programming using quadrangle inequalities" by F. Frances Yao. find
- "Speed-Up in Dynamic Programming" by F. Frances Yao. find
- "The Least Weight Subsequence Problem" by D. S. Hirschberg, L. L. Larmore. find
- "Dynamic programming with convexity, concavity and sparsity" by Zvi Galil, Kunsoo Park. find
- "A Linear-Time Algorithm for Concave One-Dimensional Dynamic Programming" by Zvi Galil, Kunsoo Park. find
Please, share your knowledge and links on the topic.











Here is another way to optimize some 1D1D dynamic programming problem that I know.
Suppose that the old choice will only be worse compare to the new choice(it is quite common in such kind of problems).
Then suppose at current time we are deal with dpi, and we have some choice a0 < a1 < a2, ..., ak - 1 < ak. then we know at current time ai should be better than ai + 1. Otherwise it will never be better than ai + 1,so it is useless.
we can use a deque to store all the ai.
And Also Let us denote D(a, b) as the smallest i such that choice b will be better than a.
If D(ai, ai + 1) > D(ai + 1, ai + 2),we can find ai + 1 is also useless because when it overpass ai,it is already overpass by ai + 2.
So we also let D(ai, ai + 1) < D(ai + 1, ai + 2). then we can find the overpass will only happen at the front of the deque.
So we can maintain this deque quickly, and if we can solve D(a, b) in O(1),it can run in O(n).
could you please give some example problems?
Hi. I'm trying to solve https://codeforces.com/contest/321/problem/E with this approach (e.g. O(n)) I know there is a solution with D&C, but I would like to try this approach.
We can easily prove quadrangle inequality: $$$C[i][j] = \sum\limits_{k = i}^j\sum\limits_{l = i}^j a[k][l]$$$
$$$C[a][d] + C[b][c] - C[a][c] - C[b][d] = \sum\limits_{k = a}^{b-1}\sum\limits_{l = c}^d a[k][l] * 2 >= 0.$$$
Now let's maintain deque $$$Q$$$ with potential candidates(opt). As we know that $$$opt[i] <= opt[i+1]$$$, so $$$Q[0]$$$ will hold the best candidate for the current time.
Let $$$Solve(i,j) = dp[i-1][0] + \sum\limits_{i}^j\sum\limits_{i}^j a[k][l]$$$
Mine approach:
1) Try to add $$$i$$$ to the candidates list. We can compare the last candidate and current:
2) Add i to the candidate list: $$$Q.pushback(i)$$$
3) Check if Q[0] is still the best answer:
4) update dp: $dp[i][1] = Solve(Q[0], i);
This approach gives me WA10. My code. Any ideas why this approach is wrong?
For question 2: The sufficient condition is: C[a][d] + C[b][c] ≥ C[a][c] + C[b][d] where a < b < c < d.
Is it quadrangle inequalities?∀i≤ j,w[i, j]+w[i+1, j+1]≤w[i+1, j]+w[i, j+1], and are these two inequalities equivalent except the >= & <=?How do you prove that if this condition is met, then A[i][j]<= A[i][j+1]?
There is one more optimization of dimanic progamming: 101E - Candies and Stones (editoral)
More Problem Collection.
you have put problem "B. Cats Transport" in "Convex Hull Optimization1", actually it belongs to "Convex Hull Optimization2"
fixed
For this moment it's the most useful topic of this year. Exactly in the middle: June 30th, 2013.
this one seemed a nice dp with optimization to me:https://www.hackerrank.com/contests/monthly/challenges/alien-languages
The problem mentioned in the article (Breaking Strings) is "Optimal Binary Search Tree Problem" , traditional one.
It can be solved by simple DP in O(N^3), by using Knuth's optimization , in O(N^2) . But it still can be solved in O(NlogN) — http://poj.org/problem?id=1738 (same problem but bigger testcases) (I don't know how to solve it. I hear the algorithm uses meld-able heap)
Are you sure that there is an O(N log n) solution to finding the Optimal Binary Search Tree Problem?
https://en.wikipedia.org/wiki/Garsia%E2%80%93Wachs_algorithm
Convex Hull Optimization 1 Problems:
APIO 2010 task Commando
TRAKA
ACQUIRE
SkyScrapers (+Data Structures)
Convex Hull Optimization 2 Problems:
Convex Hull Optimization 3 Problems (No conditions for a[] array and b[] array) :
GOODG
BOI 2012 Day 2 Balls
Cow School
Solution-Video
GOODG can be solved with Type 1
EDIT: I explain that below.
How? I noticed that, in this problem, b[j] follows no order and a[i] can be either decreasing or increasing, depending on how the equation is modeled. I was able to solve it using the fully dynamic variant, but I can't see how to apply the "type 1" optimization.
Can you add a link to your code I tried to implement the dynamic variant few weeks ago but there were so many bugs in my code :( .Maybe yours can help :/ .
Yeah, I'm sorry about saying this and not explaining. Actually I should give credit because yancouto first realized the fully dynamic approach was not necessary. Here's my code.
Maybe the most natural approach for this problem is to try to solve the following recurrence (or something similar) where f(0) = 0 and d0 = 0:
Well, this recurrence really requires a fully dynamic approach. We'll find one that doesn't. Instead of trying to solve the problem for each prefix, let's try to solve it for each suffix. We'll set g(n + 1) = 0, a0 = d0 = 0 and compute
which can be written as
now we notice that the function inside the max is actually a line with angular coefficient j and constant term aj + g(j) (which are constant on i) evaluated at - di. Apply convex trick there (the standart one) and we're done.
Notifying possibly interested people after a long delay (sorry about that again): fofao_funk, Sgauwjwjj and -synx-. And sorry in advance for any mistake, the ideia for the solution is there.
Why the downvotes? Is it wrong?
New link for Commando:
http://www.spoj.com/problems/APIO10A/
For some reason I cannot open the links with firefox because they go over the Top Rated table.
Try to zoom out, pressing Ctrl + -
One more problem where Knuth Optimization is used:
Andrew Stankevich Contest 10, Problem C.
BTW, does anybody know how to insert a direct link to a problem from gyms?
I need some problems to solve on Divide and Conquer Optimization. Where can I find them? An online judge / testdata available would be helpful.
Check this one : Guardians of the Lunatics
Learnt Divide and Conquer Optimization just from there. :P That is why I'm asking for more problems to practice. :D
Is this the best complexity for this problem? Can't we do any better? Can't we somehow turn the logL needed into a constant?
We can, using that
opt[i-1][j] <= opt[i][j] <= opt[i][j+1].Key thing is to see that opt function is monotone for both arguments. With that observation, we don't need to use binary search.
Check out my submission.
can anyone provide me good editorial for dp with bitmask .
Has matrix-exponent optimizations been included here?
Can matrix chain multiplication problem b also optimized by knuth optimization? If not, dn why?
Quote from the first of the references above:
The second reference gives O(n2) dynamic programming solution, based on some properties of the matrix chain multiplication problem.
There is also an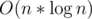 algorithm by Hu and Shing.
algorithm by Hu and Shing.
Link to the Hu and Shing algorithm?
Here is a link to a 1981 version of the thesis. The original was published in two parts in 1982 and 1984.
http://i.stanford.edu/pub/cstr/reports/cs/tr/81/875/CS-TR-81-875.pdf
However, I doubt that this will be used in competitive programming.
What are some recent USACO questions that use this technique or variations of it?
Can this problem be solved using convex hull optimization?
You are given a sequence A of N positive integers. Let’s define “value of a splitting” the sequence to K blocks as a sum of maximums in each of K blocks. For given K find the minimal possible value of splittings.
N <= 105
K <= 100
I don't think so, but I guess it can be solved by Divide And Conquer optimization.
Divide and Conquer optimization doesn't work here since the monotonicity of the argmin doesn't hold, consider e.g.
2 3 1 5. The optimal partition is[2] [3 1 5]but when you remove the5it becomes[2 3] [1].I don't get it why there is a O(logN) depth of recursion in Divide and conquer optimization ?
Can someone explain it ?
Because each time range is decreased twice.
Oh, that was very trivial.
I get it now, we spend total O(N) for computing the cost at each depth 2N to be specific at the last level of recursion tree.
And therefore O(N * logN) is the cost of whole computation in dividing conquer scheme for relaxation.
Thanks
Hello , I have a doubt can anyone help?
In the divide and conquer optimization ,can we always say that it is possible to use in a system where we have to minimize the sum of cost of k continuous segments( such that their union is the whole array and their intersection is null set) such that the cost of segment increases with increase in length of the segment?
I feel so we can and we can prove it using contradiction Thanks :)
For convex hull optimizations, with only b[j] ≥ b[j + 1] but WITHOUT a[i] ≤ a[i + 1],
I don't think the complexity can be improved to O(n), but only O(n log n) Is there any example that can show I am wrong?
I think you're right
ZOJ is currently dead. For the problem "Breaking String" (Knuth opt.), please find at here
fixed
please someone tell me why in convex hull optimization should be b[j] ≥ b[j + 1] and a[i] ≤ a[i + 1]
in APIO'10 Commando the DP equation is
Dp[i] = -2 * a * pre_sum[j] * pre_sum[i] + pre_sum[j]^2 + Dp[j] -b * pre_sum[j] + a * pre_sum[i]^2 + b * pre_sum[i] + c
we can use convex hull trick so the line is y = A * X + B
A = -2 * a * pre_sum[j]
X = pre_sum[i]
B = pre_sum[j]^2 + Dp[j] -b * pre_sum[j]
Z = a * pre_sum[i]^2 + b * pre_sum[i] + c
and then we can add to Dp[i] += Z , because z has no relation with j
the question is , since a is always negative (according to the problem statement) and pre_sum[i],pre_sum[j] is always increasing we conclude that b[j] ≤ b[j + 1] and a[i] ≤ a[i + 1]
I've coded it with convex hull trick and got AC , and the official solution is using convex hull trick
someone please explain to me why I'm wrong or why that is happening
thanks in advance
if b[j] >= b[j + 1], then the technique is going to calculate the minimum value of the lines, if b[j] <= b[j + 1], then it's going to calculate the maximum value of the lines, as this problem requires.
Is it necessary for the recurrence relation to be of the specific form in the table for Knuth's optimization to be applicable? For example, take this problem. The editorial mentions Knuth Optimization as a solution but the recurrence is not of the form in the table. Rather, it is similar to the Divide-and-Conquer one, i.e. dp[i][j] = mink < j{dp[i - 1][k] + C[k][j]}. Does anyone know how/why Knuth's optimization is applicable here?
It is also worthwhile to mention the DP Optimization given here http://codeforces.com/blog/entry/49691 in this post.
Can we have the same dp optimizations with dp[i][j] = max (dp....)?
Yes.
In that case (dp[i][j] = max (dp...) ) the condition still unchanged : A[i][j] ≤ A[i][j + 1]. Is that true? Thanks!
Yes.
can someone please give me intuition on proof of A[i, j - 1] ≤ A[i, j] ≤ A[i + 1, j] given for knuth optimization of optimal binary search tree.
Fresh problem. Can be solved with CHT.
What will be the actual complexity of Knuth optimization on a O(n^2 * k) DP solution ? Will it be O(n^2) or O(n*k)? Here n = number of elements and k = number of partitions.
I would like to mention Zlobober, rng_58, Errichto, Swistakk here politely. It would be really helpful if you kindly answered my query.
It can only remove n from the complexity because it (more or less) gets rid of iterating over all elements of the interval (up to n elements).
Thanks a lot for replying to me. So what you are saying is — a O(n^2 * k) solution will turn into a O(n * k) solution? I got TLE in problem SPOJ NKLEAVES (n=10^5, k=10) using Knuth optimization, but passed comfortably using divide & conquer optimization in O(n k log n). That's why I am curious to know whether knuth optimization reduces a n factor or a k factor from the original O(n^2 * k) solution, since a O(n*k) solution should have definitely passed. Would you please have a look?
Can you show the code? I'm not sure but I think that Knuth optimization can be used here to speed up the O(n3·k) solution with states dp[left][right][k]. The improved complexity would be O(n2·k).
How does it help in any way xd?
He asked if N or K will be removed from the complexity, I answered. What is wrong here?
You said "at most n" what brings 0 bits of information since k<=n.
It is O(n2) as the complexity upper bound is proven by summating the running time of DP value calculation over the diagonals of the n × k DP matrix. There are n + k - 1 diagonals, on each of them running time is at most O(n) due to the given inequalities, so the total running time is O((n + k)n) = O(n2).
Someone know where i can find an article about Lagrange optimization? (i know that this can be used for reduce one state of the
dpperforming a binary search on a constant and add this on every transition until the realized number of transition for reach the final state become the desired)I know this can be treated as off-topic by many of us, but what about solving DP states which are direct arithmetic (specifically sum/difference) of previous states:
Say the DP state is 1D, like in Fibonacci series (
dp[i] = dp[i-1] + dp[i-2]), we already know of a solution inO(k^3 * log n)using matrix binary exponentiation, wherekrepresents thatdp[i]depends ondp[i-1], dp[i-2], .. dp[i-k].Is there an optimisation for 2D states like the same? Say the state is as follows:
I am finding it hard to reduce it to any less than
O(n * m)for findingdp[n][m]I guess you should ask it after the Long Challenge
.
Yeah I Agree, I was also trying to solve it.
I found a good Tutorial on 2d-dp Matrix Exponentiation.
https://www.youtube.com/watch?v=OrH2ah4ylv4 a video by algorithms live for convex hull trick. The link given for convex hull optimization is dead now please update.
use this archive https://web.archive.org/web/20181030143808/http://wcipeg.com/wiki/Convex_hull_trick
I know it's necroposting, but still. Can anyone give a link to tutorial or something(in English) for the trick used in IOI16 Aliens problem?
Here's a similar problem with a nice description of the algorithm used
Can someone help me prove that the sufficient conditions for Divide and Conquer Optimization are satisfied in this problem.
I was able to solve it using the same technique with some intuition. But wasn't able to formally prove it.
Define $$$dp_{i,j}$$$ to be the minimum cost if we split the first $$$i$$$ plants into $$$j$$$ groups.
where $$$cost_{k,j}$$$ is the cost of grouping plants from $$$k$$$ to $$$j$$$. Assume that for certain $$$j$$$ the optimal $$$k$$$ for the formula above is $$$\hat k$$$ i.e. $$$dp_{i,j} = dp_{i-1,\hat k} + cost_{\hat k+1,j}$$$ and for any $$$k<\hat k$$$:
Advance $$$j$$$ to $$$j+1$$$. Take any $$$k<\hat k$$$ and prove:
But this is not hard to see since:
which is true because adding plant $$$j+1$$$ to a bigger group of plants from $$$k+1$$$ to $$$j$$$ certainly costs no more than adding plant $$$j+1$$$ to a smaller group of plants from $$$\hat k+1$$$ to $$$j$$$.
This shows that when we advance $$$j$$$ to $$$j+1$$$ we can ignore any $$$k<\hat k$$$ which allows us to apply divide and conquer.
Please update link of Convex Hull Optimize1 that link is now dead.
https://web.archive.org/web/20181030143808/http://wcipeg.com/wiki/Convex_hull_trick
I solved Problem 1. Redistricting from the Platinum division of the USACO 2019 January contest in
O(n)using the deque optimization described in this comment while the official solution isO(n log n).First, for each suffix, we compute the number of Guernseys minus the number of Holsteins and store it in the
suffixarray. We definedp[i]to be the minimum number of Guernsey majority or tied districts with the firstipastures. Sodp[i] = min(f(k, i)) for k < i, wheref(k, i) = dp[k] + (suffix[k] - suffix[i + 1] >= 0). For two indicesa < b, ifdp[a] > dp[b], thenf(a, i) >= f(b, i)for anyi > b. The same is also true ifdp[a] == dp[b] && suffix[a] >= suffix[b]. In all other cases,f(a, i) <= f(b, i)for alli > b. We'll definebad(a, b) = dp[a] != dp[b] ? dp[a] > dp[b] : suffix[a] >= suffix[b]which is true ifawill never be the optimal value forkin the future.We can maintain a deque
qsuch that!bad(u, v) for u < v. Before we insert a new indexi, we pop off indices from the end of the queue whilebad(q.back(), i)since those indices will never be better thani. After popping off indices from the front of the deque which are more thanKaway fromi, the optimalkvalue is always at the front. Both the loops popping from the front and back are amortizedO(1)since there are a total ofNindices, each of which can only be popped off at most once. This makes the solutionO(n).orz indy256 meta-san. optimizing the optimization technique itself?
Cp-algorithms has added official translation of Divide and Conquer Optimization, thought it might be useful to add. https://cp-algorithms.com/dynamic_programming/divide-and-conquer-dp.html
Also exists Alien's optimization (link1, link2).
iShibly
Can anyone explain how to bring the DP of NKLEAVES to the form of Convex Hull Optimization 2 from above? More specifically, how to I define $$$b$$$ and $$$a$$$ from $$$dp[i][j] = \min\limits_{k < j}(dp[i - 1][k] + b[k] \cdot a[j])$$$ so that $$$b[k] \geq b[k + 1]$$$ and $$$a[j] \leq a[j + 1]$$$?
My DP so far is $$$dp[i][j] = \min\limits_{k < j}(dp[i - 1][k] + cost(k, j))$$$ where $$$cost(k, j)$$$ is the cost to move leaves from $$$(k+1)$$$-th to $$$j$$$-th into a pile at location $$$j$$$. After some simplification, we have:
where $$$sum(k) = \sum\limits_1^k w(i)$$$ and $$$wsum(k) = \sum\limits_1^k i \cdot w(i)$$$ which we can precompute.
If we fix $$$j$$$ then in the formula above, $$$sum[j] \cdot j - wsum[j]$$$ is a constant that we can ignore and focus on $$$-sum(k) \cdot j + wsum(k) + dp[i - 1][k]$$$ and for each $$$k$$$ define a line $$$hx + m$$$ where $$$h = -sum(k)$$$ and $$$m = wsum(k) + dp[i - 1][k]$$$. We then use CHT to get values for all $$$j$$$ on $$$i$$$-th row in $$$O(n)$$$ time.
But it still baffles me how to bring my formula to the neat one in the post.
Actually, right under the table in the post the author wrote:
I slightly disagree with the second part, $$$F[j]$$$ is just computed from $$$j$$$ and not from $$$dp[j]$$$ but that's just being nitpicky with notations. Applying that to NKLEAVES we get:
where $$$C = sum[j] \cdot j - wsum[j]$$$ is a constant when we fix $$$j$$$, $$$F(k) = wsum(k) + dp[i - 1][k]$$$, $$$b(k) = -sum(k)$$$, $$$a(j) = j$$$. It's not hard to see that $$$b$$$ is a decreasing function and $$$a$$$ is an increasing function while $$$F$$$ is computable in $$$O(1)$$$.
Sorry if I misunderstanding your questions, but here are some DP-optimization techniques
1. DP-bitmask
By storing all states by bit numbers, in most problems, you can have some bitwise tricks that reduce both constant time (calculating by bitwise cost less) and complexity ($$$O(f(x))$$$ -> $$$O(\frac{f(x)}{w})$$$, $$$w$$$ is normally use as $$$wordsize = 32$$$)
2. Space-optimization
In some problems where we only care about $$$f[n][..]$$$ and $$$f[n][..]$$$ depends on $$$f[n - 1][..]$$$ then we can reduce to $$$2$$$ DP-array $$$f[0][..]$$$ & $$$f[1][..]$$$ (reduced $$$O(n)$$$ times of space)
Some other linear reccurence $$$f[n][..]$$$ depends on $$$f[n][..], f[n - 1][..], ... f[n - k][..]$$$ and when $$$k$$$ is much smaller than $$$n$$$ we can use this trick with $$$k$$$ DP-array (reduced $$$O(\frac{n}{k})$$$ times of space)
3. Recursive-DP with branch-and-bound
Normally Iterative-DP runs faster than Recursive-DP. But in some specific case as $$$Knapsack_{\ 0/1}$$$ problem, where we can have some good observations with optimizing algorithm by remove as many not-good cases as possibles. We can have much fewer cases to take care for.
Ofcourse in some cases it will break the $$$space-optimization$$$ tricks, and we have to store data by another ways to reduce the time (like using global variables, passing reference data)
4. DP-swaplabel
Sometimes by changing DP-states will results in another way of computing the results, thus will change the complexity
** 5. Alien trick**
Can you add ioi 2016 alien's trick to the tables with the conditions required to be satisfied for the trick to be used ?
There's one more optimization idea which came in one of the recent contests as well.
Consider dp[i] as array of n points.
Now, if recurrence is as follows:
dp[i] is a linear combination of different j values of dp[i-1] and where coefficients are independent of j.example: dp[i][j] = dp[i-1][j1] + c_1(i)*dp[i-1][j2] + c_2*dp[i-1][j3]+.....
we can do this naively in O(N^2), But to optimize it, one can use FFT algorithm treating dp[i] and dp[i-1] as polynomials.
for example: consider the recurrence: dp[i][j]= 2*dp[i-1][j-1] + 3*dp[i-1][j] and we need to find dp[n][j0]
so, let A= [3 2] => a(x) = 3 + 2*x and B = vector(dp(i-1)) => b_i(x) = dp[i-1][0] + dp[i-1][1]*x + dp[i-1][2]*x^2 +....+dp[i-1][j-1]*x^(j-1) + dp[i-1][j]*x^j +....+dp[i-1][n]*x^n.
Now, to get dp[i][j] we can multiply the above polynomials to get C=A*B, and then dp[i][j] will be the coefficient of x^j. This can be done in O(N*logN) using FFT.
But doing this N times will get TC O(N*N*logN)
Now, how to optimize this?
if dp[0] (base array) is all 1. so, dp[n] will be product of a(x) n times.
This can be done using Divide and conquer in O(N*logN*logN)
This is one of the idea to optimize recurrence using FFT.
Problem that can be solved using this technique: Colourful Balls-codechef
You forgot Aliens Trick :)