Online Round 3 and its analysis were prepared by Chmel_Tolstiy, aropan, Romka, SobolS, Ra16bit, snarknews and Gassa.
During the third round of “Yandex.Algorithm” 265 participants have made at least one attempt, 177 of them solved at least one problem. There were 559 attempts for A (137 successful), 127 attempts for B (47 successful), 111 attempts for C (64 successful), 64 attempts for D (15 successful), 45 attempts for E (20 successful) and 606 attempts for F (129 successful).
Problems of the Round 3 proved to be easier on average than the problems of the first two rounds, and it became apparent during the contest that the winner would probably solve all problems. Indeed, Petr has solved all problems by the 72nd minute, although all of them were submitted “open”. Five minutes till the end of the contest KADR takes 2nd place with 6 problems, he has also solved all problems “open”. But almost immediately nkurtov (Nikolay Kurtov, Switzerland) solves his 6th problem and takes 1st place, as he has solved three problems “blind”. Two minutes before the end of the contest winger takes place with two problems submitted “blind” in the beginning of the round and all others submitted “open”. And at the last minute s.quark (s-quark) from China submits problem E “blind” and takes the first place: he has submitted only B “ open”. Overall five participants have solved all problems before the system test: s.quark is 1st, nkurtov — 2nd, winger — 3rd, Petr — 4th and KADR — 5th.
After the system tests it turns out that s.quark's F which he submitted “blind” on the 25th minute failed. Also nkurtov's С and D failed. Both winger's “blind” solutions passed, so he took the final 1st place in the Online Round 3. Petr took the 2nd place, but he had already qualified to the finals before. KADR stayed at the 3rd place, ainu77 (ainu7) from South Korea moved to 4th, and s.quark still took 5th place even after failing a problem and qualified to the final round.
Problem A (Candy Mood)
Let us count the number of candies M that are not tasty. If M = 0, the answer is  . Otherwise, consider the expected increase in the mood braught by i-th candy if it is tasty. It can be equally probable in M + 1 positions relative to the not tasty candies, and only in one case you will eat the tasty one. So, the expected increase in the mood braught by one tasty candy Ai is equal to
. Otherwise, consider the expected increase in the mood braught by i-th candy if it is tasty. It can be equally probable in M + 1 positions relative to the not tasty candies, and only in one case you will eat the tasty one. So, the expected increase in the mood braught by one tasty candy Ai is equal to 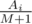 . For candies that are not tasty the expected change in the mood is
. For candies that are not tasty the expected change in the mood is 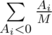 , as each of the not tasty candies can become the first not tasty candy. Overall, the expectation of the mood change is equal to
, as each of the not tasty candies can become the first not tasty candy. Overall, the expectation of the mood change is equal to 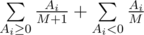 .
.
Problem B (Marbles)
Without loss of generality we will assume N ≤ M.
Let us consider the case N = 1. Denote the number of marbles on the photo by k. Note that we can keep any k marbles. But we cannot get all possible relative positions, because we cannot change their relative order. We can choose any k positions and place marbles on them, though. So, there are 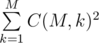 different possible photos.
different possible photos.
Let N ≥ 2. Then if there are k = N·M marbles, we can get only one such photo, because we didn't make any move (the first move necessarily removes one marble from the field). If k = N·M - 1, then after the first move we can only move to the free cell on the field — it is equivalent to the well-known brainteaser “15 puzzle”; in this case, exactly half of the permutations are reachable (see the link above). If k < N·M - 1, let us consider any two free cells, first get a configuration where they are adjacent. Then the “15 puzzle” is solvable for one of them (it depends on the sum of the number inversions in the permutation and the numbers of row and column of the free cell, and the sum of numbers of row and column differ by one for adjacent cells). Then, choosing the right free cell, we only have to solve the “15 puzzle”.
Thus, the overall number of photos is 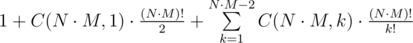 .
.
Problem C (Fan Placement)
The easiest way of solving this problem was to generate all possible permutations of the fans. Let us fix an order of fans, for example, from bottom to top, and let i-th fan have initial number pi. Obviously, if for each fan the fan immediately before him does not block the view, then everybody sees the field comfortably. Let us consider all pairs of adjacent fans. If hpi ≤ hpi + 1, then this pair does not create any limitations on the placement: for any placement of the fan pi + 1 fan pi will not block his view because pi is lower. If hpi > hpi + 1, there appear the following restrictions: fan pi + 1 cannot take the next hpi - hpi + 1 rows after the fan pi. So, these hpi - hpi + 1 rows should be removed from the consideration for this fixed order of the fans. After performing this operation for all adjacent pairs of fans, we should add the number of combinations of K out of the number of rows left, where K is the total number of fans. To make this operation fast, we precompute the table of values Cnk for n and k not exceeding 1000.
Time complexity: O(n2 + k!·k).
There is a harder way using dynamic programming where the state is triple “how many rows already considered, mask of seated fans, number of the last fan”. Transition in this case consists of iterating through the “pre-last seated fan”. For this solution to work fast we have to store a table of cumulative sums parallel to the dynamic programming table to avoid inner loop through the rows.
Problem D (Interesting Language)
Let us first describe the bruteforce solution. Find all pairs of words such that one of them is a prefix of another. Remove the shorter word from the longer one, leaving only the suffix. If we compute for each suffix how many ways are there to get it using this operation and denote the number of ways by cntsuff, the answer for the problem is 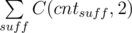 , where the sum is over all suffixes.
, where the sum is over all suffixes.
To compute for each suffix the number of such pairs let us use a trie. Let us build two tries based on the input array of words: the first one will contain all the input words, and the second one will contain all the reversed words. Go through the nodes of the trie with reversed words. Each time we enter a terminal node, go up from this node to the root while in parallel going down using the same symbols in the trie with the input words. If we enter a terminal node in the trie with input words during this process, we should increase by one the counter for the suffix where we are at the moment in the trie with reversed words. If we've left the trie with input words during the process, we can stop.
After such pass through the trie there will be the correct value cntsuff in each node of the trie, and we just have to compute the answer using the formula above.
Time complexity: O(sumL), where sumL is the sum of lengths of all words.
Problem E (Taxes and Roads)
Let us see what paying the tax in some city gives us. After paying the tax in city A we can visit some other cities free of charge. Those are cities that are reachable from A and from which A is also reachable. If we get from the cities to graph theory, we can say that we can now visit free of charge all the vertices from the same strongly connected component of A. So, if we find the strongly connected components in the initial graph, we can pay the tax only when entering each component. As entering a strongly connected component “opens” for free of charge travel all the component and all taxes are non-negative, it will never be profitable to pay the tax in any other city of the same component.
Let us build a new graph based on the initial one. Its vertices will correspond to the strongly connected components of the initial graph. The weights of the edges will be set the following way: for each pair of strongly connected components that have an edge between them in the initial graph, create an edge in the new graph with the weight equal to the minimum of the taxes in all the cities which are the endpoints of the edges connecting this pair of components in the initial graph. Of course, we should account for the orientation of the edges.
After the new graph is built, we need to find the shortest path between the vertices that correspond to the strongly connected components which contain vertices 1 and n of the initial graph. It can be done either using the Dijkstra algorithm or by dynamic programming taking into account that the new graph is a directed acyclic graph. We also have to consider the start of the trip separately, as one can only pay the tax when he enters a city.
Problem F (Place for Capital)
If the angle between the radii is more than two radians, the minimum distance is the sum of radii. Otherwise, it is the difference of radii plus the length of the arc passing through the point with smaller radius. It follows from the fact that in the “curvilinear trapezoid” made out of two radial edges and two arcs the shortest path between the opposite nodes is the path through a radial edge and the arc of smaller radius.
We are left to compute everything accurately. Usage of the atan2() function allows to surpass most of the pitfalls. Without using atan2() there are problems with precision in case of two close points with big radii; in this case it helps to use asin instead of acos to avoid loss of precision.












