336A - Vasily the Bear and Triangle
val = |x| + |y|. Then first point is (val * sign(x), 0), second — (0, val * sign(y)). Swap points if needed according to statement.
Let's see why this is the answer. Conditions x ≠ 0 and y ≠ 0 give us that one point is on X-axis, and the other on Y-axis. Let's see how it works for x > 0 and y > 0. Other cases can be proved in similar way. We need to show, that (x, y) belongs to our triangle(including it's borders). In fact (x, y) belongs to segment, connecting (x + y, 0) with (0, x + y). Line through (x + y, 0) and (0, x + y) is Y = - X + x + y. Using coordinates (x, y) in this equation proves the statement.
336B - Vasily the Bear and Fly
Also you could iterate circles, adding distance for each of them and dividing by m2 in the end. Let's see how the i-th iteration works 1 ≤ i ≤ m. Distance to m + i-th circle is 2R. Distance to m + j-th circle, where |j - i| = 1, is  . For other circles it's quite simple to calculate sum of distances. There are i - 2 circles which located to the left of current circle. So, sum of distances for these circles is
. For other circles it's quite simple to calculate sum of distances. There are i - 2 circles which located to the left of current circle. So, sum of distances for these circles is 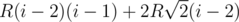 . In the same manner we can calculate answer for cirlcles which are located to the right of the current circle
. In the same manner we can calculate answer for cirlcles which are located to the right of the current circle

336C - Vasily the Bear and Sequence
Let's check max beauty from 29 to 0. For every possible beauty i our aim is to find largest subset with such beauty. We will include in this subset all numbers, that have 1 at i-th bit. After that we do bitwise and as in statement, and if the resulting value is divisible by 2i, then there is the answer. Solution works in O(n).
336D - Vasily the Bear and Beautiful Strings
any — random binary string, s + g — concatenation of strings, MOD = 1000000007.
String 1 + any always transforms into 0, string 1 — into 1. String 01 + any always transforms into 1, string 01 — into 0. String 001 + any transforms into 0, string 001 — into 1, and so on. Using these facts let's consider following solution.
Cases like strings without ones or zeroes are easy. For every i (in zero-based numbering) let's assume that it is position of the first occurence of 1 in our string. Using already known facts we can understand what is the final result of transformations for such string. If the result equals to g, we add C(cnt[0] + cnt[1] - i - 1, cnt[1] - 1) to the answer. Calculation of binomial coefficients is following: fact[i] = i!%MOD, 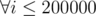 , C(n, k) = fact[n]inv(fact[n - i]fact[i]), where inv(a) — inverse element modulo MOD. inv(a) = aMOD - 2, because MOD is prime number.
, C(n, k) = fact[n]inv(fact[n - i]fact[i]), where inv(a) — inverse element modulo MOD. inv(a) = aMOD - 2, because MOD is prime number.
336E - Vasily the Bear and Painting Square
Pretty tough problem. Consider following DP dp[lvl][op][cur][type] — number of ways to take op triangles, if we have 2lvl + 1 squares. cur, type — auxiliary values. Answer will be dp[n][k][0][2]k!. type means type of transitions we make. cur — amount of used quarters (cur = 4 — 2 quarters, cur < 4 — cur quarters). It is important to distinguish cur = 2 from cur = 4, because amount of consecutive pairs of unused quarters is different.

About transitions. type = 2. Iterate amount of pairs (considering cur) of consecutive quarters that we will take. It is important for them to have no common quarters. We can get two pairs only in case cur = 0. Let's also take some quarters that are not in pairs. Calculate number of ways to select corresponding triangles and add to the current DP-state value dp[lvl][op - choosen][newcur][1] * cntwaystochoose. For better understanding of type = 2 check my solution (calc(n, k, cur, type) — isfordp[n][k][cur][type]).
type = 1. Now we take triangles at the borders (number of squares is 2*lvl + 1). "at the borders" means marked X, see the picture.

Iterate amount of pairs (considering cur) of consecutive triangles we take. It is important for pairs to have no common triangles. Let's also take some triangles that are not in pairs. Calculate number of ways to select corresponding triangles and add to the current DP-state value dp[lvl][op - choosen][cur][0] * cntwaystochoose.
type = 0. We take triangles at the borders (number of squares is 2*lvl). "at the borders" means marked X, see the picture.

Take some triangles, not in pairs. Calculate number of ways to select corresponding triangles and add to current DP-state value dp[lvl - 1][op - choosen][cur][2] * cntwaystochoose. Starting values: dp[0][0][cur][1] = 1, dp[0][cnt][cur][1] = 0, cnt > 0.











for Problem 336A, 4th condition is that the area of triangle should be minimum, for test case 1 (x=10,y=5) point 'A' should be A(0,10) and point 'C' should be C(20,0) which gives the smallest area of triangle ABC (0.5*20*10 = 100) but answer is given as point A(0,15) and C(15,0) which gives area of triangle as 0.5*15*15 = 112.5, please tell me what I m missing?
It's should be isosceles triangle.
The triangle needs to be Isosceles.
you have to choose such points so that other two angles i.e ACB and BAC should be 45 degree.If you chose other point then angle will be different.For example in first test case we are finding x1,x2,y1,y2 using trigonometry formula i.e. tanθ = perpendicular / base. Suppose D is point having coordinate x and y.From point D we make a perpendicular to line BC and AB and name these point as E and F resp.we know BE = x = 10 and FB = y = 5,we have to find EC (BC = BE + EC) ? , we use tan formula to get FB/EC = tanθ here θ = 45 degree so EC = FB = 5(tan 45 = 1); so x2 = BE + EC = 15; Similarly we find AF(AB = AF + FB), AF/BD(BD = BE = 10) = 1(tan45 = 1) so AF = 10; y1 = AF + FB = 15;
gridnevvvit May you please tell us the manner in which these geometric shapes are generated? I think they are really elegant.
The pictures are broken, please fix them.
In problem C: we have b1 and b2 and ... and bk = 0, is it an accepted answer? 0 mod n = 0 with any n.
For Problem B it is mention that experiment repeats for m^2 days. But in authors solution the experiment is running only for m days. Please tell me am i missing something..
Experiment is running m2 days. Authors calculate answer by using following idea. We fix some circle with index i (1 ≤ i ≤ m). After that we calculate sum of of distances to circles with indexes m + j (1 ≤ j ≤ m) by using formula.
in problem C you have written: after doing bitwise AND of all numbers whose ith bit is set, we have to divide it by 2^i. Can there be a case when it is not divisible by 2^i but divisible by for some other power of 2?
It is possible that the bitwise-AND result of numbers with the ith bit set to 1 might be divisible by 2^j, j!=i. But let us analyse what such j's can be.
Case 1: j>i. If the set chosen for i is such that the jth bit = 1 for all numbers in that set, then this set will indeed be divisible by 2^j. But, since we are iterating i from 29 to 0, this particular j (>i) would already have been considered and a set with equal or greater no. of elements as compared to the set corresponding to i would already have been found out.
Case 2: j<i. Again, since we are iterating i from 29 to 0, we need not consider the case that the result obtained by bitwise AND of the set corresponding to i will be divisible by 2^j since this will be checked in future iterations of i when it is decremented further till i=j. Here, we may end up with this same set only or perhaps an even larger set which is perfectly divisible by 2^j.
To sum up, though the set under consideration might be divisible by 2^j (j!=i), but we need not consider divisibility by j's != i since this has already been/will in future be checked. Hope, this clarifies the issue.