Please help me to solve this task. I try solve it but I couldn't.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 162 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/25/2024 15:54:56 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











The problem is easy. You just want to use arrays and variables
really EASY?
btw seems to be splay tree.
We have a rooted tree. For every node of the tree, we want to choose as many vertices of its subtree (descendants) as possible, such that the sum of their salaries doesn't exceed the budget. Then, we can find the best result by trying all possible managers.
It's clear that we always want to take some k descendants with lowest salaries. So we can go from the node with lowest salary (out of all) to highest, and always add it to all the vertices on the path from that node to the root, for which the resulting sum doesn't exceed the budget. This way, we could use a simple simulation in O(N2).
That's not good enough, but a decent start. First, realize that if we can't add to some node, we can't add to any of the nodes above it (proof left as exercise to the reader). We can do a heavy-light decomposition, and build a BIT (Fenwick tree) above every path. That allows us to add to many nodes quickly, and to find the sum in any node. Now, adding is simple: just iterate over all individual paths that are traversed from a node to the root, and if we enter a path at node with depth (from the top of the path) x, then add the salary to top x nodes of that path.
That still doesn't answer how to detect nodes for which we'd overflow the budget. But we can observe that it'll happen for several (possibly zero) nodes on top of some path, and for all nodes we traverse above that path. Let's mark the nodes for which we've already overflown as dead; for every path (from the decomposition) we get to, we'll go from down the topmost living node in it and mark the nodes as dead until we find a node which doesn't overflow (or isn't on the path from the starting node to the root), and mark those that do as dead. Then, just add to the top x nodes of this path, including the dead ones (those don't bother us anymore).
We only mark a node dead at most once, but need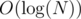 time to find out the sum in a node and to update a path; from every node, we get to
time to find out the sum in a node and to update a path; from every node, we get to 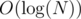 paths, which we need to update, so the total time is
paths, which we need to update, so the total time is 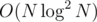 .
.
So no splay tree here. But I used a similar trick in 342E - Ксюша и дерево.
Does anyone know how fast this code works for this problem? (It passed all tests. But I don't know the complexity of this method.). (-_-).
It's complexity is O(nlg^2n) since you are merging from small map to large map.
I cannot find the old code, but I remember that I solved it by iterating through all possible roots then use binary search + a segment tree. Time complexity O(Nlog^2(N)).
If you have a segment tree which includes all ninjas in this subtree, we can easily check how much ninja we can take from this subtree, with binary search + segment tree in O(n * log(n)) (If you do binary search outside of segment tree it will be O(n * log2(n)).
All we need is merging our children's segment trees. When you merging two segment tree that their sizes are x and y, add small one to big one. Complexity will be O(n * log2(n)). (O(n * log(n)) from merging and O(log(n)) for adding ninja in a segment tree.)
I think everyone is discussing about O(nlg^2n) solution. I also coded of that solution but I got TLE. (I used slower online judge.)
However the O(nlgn) solution for that problem is very simple. Think about this : Why should we hold the data structure in recursion stage? Can't we use a simple RMQ in global space, and pop the ninjas when we need them?
I can't get your solution. Why we use RMQ, and what is the "pop the ninja"? :(
Let's think about simple greedy strategy first.
Do dfs with priority queue and merge the heaps as the method we discussed. If the merged set has more than M salaries, we can simply pop some ninjas with highest salary. It takes O(nlg^2n) time.
Now we can observe that, doing dfs with priority queues are unnecessary in this problem. We can simply use RMQ in global space, and pop some ninjas with highest salary in dfs preorder range.
This is my nlgn code : http://codepad.org/Ra72tyQt
The important part is, if this ninja is unnecessary in this subtree, it will be unnecessary for parents of this nodes. Thanks!