350A - TL
Let's v = min(ai), p = max(ai), c = min(bi). So, if max(2 * v, p) < c, then answer is max(2 * v, p), else answer is - 1.
Author solution: 4632352
350B - Resort
Input data represents a graph, by using a array of parents of every vertex. Because every vertex has at most one parent, we can use following solution: we will go up to parent of vertex v (prev[v]) until not found vertex with the outcome degree ≥ 2. It is better to calculate outcome degrees in advance. After all, we will update the answer.
This algorithm works in O(n).
Author solution: 4632399
350C - Bombs
First of all, Let's sort all point by increasing of value |xi| + |yi|, all points we will process by using this order. We will process each point greedily, by using maximum six moves. Now we want to come to the point (x, y). Let's x ≠ 0. Then we need to move exactly |x| in the dir direction (if x < 0 the dir is L, x > 0 — R). Similarly we will work with y-coordinates of point (x, y). Now we at the point (x, y), let's pick a bomb at point (x, y). After that we should come back to point (0, 0). Why it is correct to sort all point by increasing of Manhattan distance? If you will look at the path that we have received, you can notice that all points of path have lower Manhattan distance, i.e. we will process this points earlier.
This solution works in 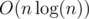
Authors solution: 4632478
350D - Looking for Owls
It's possible to solve this problem by using only integer calculations. Normalization of the line Ax + By + C is following operation: we multiply our equation on the value 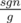 , where g = gcd(A, gcd(B, C)), if A < 0 (orA = 0andB < 0) then sgn equals to - 1, else sgn equals to 1.
, where g = gcd(A, gcd(B, C)), if A < 0 (orA = 0andB < 0) then sgn equals to - 1, else sgn equals to 1.
Now the solution. We will have two maps (map<> in С++, TreeMap(HashMap) in Java) to a set of points (it's possible that some points will have multiply occurrence into the set). In first map we will store right boundaries of the segments, in second — left boundaries (in increasing order).
In advance for every segment we will build a normalized line, and for this normalized line we will put in our maps left and right segments of the segment.
After all, for every fixed line let's sort our sets.
Let's fix two different circles. After that, let's check that distance beetween them is greater then sum their radiuses, also you should check that circles has same radius. We can assume that we builded a line between centers of circles (x1, y1) and (x2, y2). Perpendicular to this line will have next coefficients (center of the segment [(x1, y1), (x2, y2)] also will belong to the next line) A = 2(x1 - x2), B = 2(y1 - y2), C = - ((x1 - x2) * (x1 + x2) + (y1 - y2) * (y1 + y2)). After that you need to calculate values cntL, cntR by using binary search on set of points that lie on this line. cntL — amount of left boundaries that lie on the right side of point ((x1 + x2) / 2, (y1 + y2) / 2), cntR -- amount of right boundaries that lie on the left side of the point ((x1 + x2) / 2, (y1 + y2) / 2). After that you should add to answer value cntV - cntR - cntL,l where cntV — amount of segments, that lie on the nolmalized line.
Total complexity: 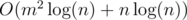 .
.
solution: 4632546
350E - Wrong Floyd
Let's do the following: construct the graph with the maximum possible number of edges and then remove the excess. First of all, you can notice that if k = n answer is - 1. Else let's fix some marked vertex, for example a1. Let's put in our graph all edges except edges beetween a1 and x, where x — an another marked vertex.
So, why this algorithm is correct? If Valera's algorithm is wrong, then there are a ''bad'' pair of vertexes (i, j). ``Bad'' pair is a pair for that Valera's algorithm works wrong. So, there are not marked vertex v on the shortest path from i to j, and v ≠ i, and v ≠ j. Without loss of generality, we can assume, that distance beetween i and j equals to 2, but Valera's algorithm gives greater answer. There are some cases, that depends on the type of vertexes i, j. But we can look only at the case where (i, j) are marked vertexes. First, add to the graph all edges beetween not fixed (i, j) vertexes. Second, add to the graph edges beetween some fixed vertex (i or j) and some not marked vertex. Third, add to the graph edges beetween i and some marked vertex v, where v ≠ j. It's simple to understand, that if we add some another edge, the Valera's algorithm will work correctly. Total amount of edges is  .
.
BONUS Simple bonus. For same contrains (n, m, k) can you build a graph, where Valera's code works correctly?
Код: 4632600











For E Bonus: for k>=1, build a star with any marked vertex(i.e. all nodes are connected directly to marked vertex k.),then continue to build extra edges until the number of edges = m.
Proof: it is clear that the maximum value of pair-wise distance of nodes <= 2 in a star. Also, distance = 1 if and only if there is a path directly connecting those two nodes.(even though the two nodes are both unmarked, their distance is defined as 1 if they are directly connected.) If there are no path between two nodes, the marked node will also provide a "island" for them to finish a path with distance 2. therefore the graph is correct.
k=0 is possible if and only if (m==(n*(n-1))) or (m<=n/2)
C can also be solved by sorting based on the values of |x| and |y|. :)
thanks
Hello Sir Why doesn't it work if sort it according to x and y axis
You might have got the solution by now .
But if you didn't then here is how .
Let's consider Bomb positions ( after sorting) = { (-3,-3) ,(-3,-2),(-2,-3) }
So you do the operations to diffuse bomb at position (-3 , -3 ) first . And for this you will have to go either through (-2 , -3) or (-3,-2) which isn't allowed .
PS : You can also change the direction of your path that is you can move to other points to avoid (-2 , -3) or (-3 , -2 ) but again that will require more direction changes which increase the total number of operations .
My solution for C problem in java is similar to author's solution but I am getting Time out for the solution. Don't know where am I doing the heavy operation. My solution id is 4639684
I think it's just because of System.out.println("..");. You can use String builder instead.
Thank you! I tried and it worked. So thanks and lot and Sorry for trying it so late.
does that apply to cout in c++ because I also solved it in the same way and I am getting TLE , here is my submission
Not to cout, but to endl. Use '\n' instead.
ok , thanks :)
i found the statements very hard to understand for example on problem E it sais that the graph shoud not contain any loops, what i get from this is that the graph is a tree , also i couldnt get the statement on problem B . i know my english sux but still...
I couldnt get the statement on problem B too.
D is a great problem, I've learned a lot from it. Thx!
Does anyone feel that statement in problem A is not accurate ? In the below statement:
all wrong solutions do not pass the system testing;
my understanding is that there exists a wrong solution that does not pass the system testing,
But as per the solution to the problem, it means that
no wrong solutions pass the system testing;
i.e., all wrong solutions fail the system testing.
i also find it difficult to understand, btw i did even understand the example of input and output