The solution doesn't exist only if the mimimal way to bribe is grater than n. Otherwise we can increase the gift price to make price1 + price2 = n.
Let's find the miminal way to bribe. We should buy that gift for old lady which costs less. It means, if we have 2 guards with params a b c d, then minimum bribe price will be min(a, b) + min(c, d). Let's choose the guard with the minimal bribe price. If the minimal bribe price is greater than n, answer -1. Otherwise, the possible answer is, for example: Guard number, min(a, b), n–min(a, b).
Dima can make k–1 tasks, so Inna always tells him off for each k-th taks, beginning from the chosen place. So for the numbers with same modulo by k the answer will be the same. We should find the answer with minimal first task number so it is eniugh to calculate the sums of “tellings of” for tasks 0, 1... k–1. We can do it in such way: Determine the array int sum[k]. And put the number into appropriate bucket while reading:
sum[I mod k] + = a[i]. Now we should simply find first i with minimal sum[i].
Complexity: O(N).
Let's calculate dinamic: d[num][balance] where num – last looked fruit, balance — difference between sum of colories and sum of tastes. Let's multiply each b by k. The answer will be d[n][0].
d[num][balance] = maximal possible sum of tastes under conditions.
Step: from d[num][balance] we can relax answers:
d[num + 1][balance] = max(d[num + 1][balance], d[num][balance]) – if we don't choose a fruit
d[num + 1][balance + a[i] - b[i]·k] = max(d[num + 1][balance + a[i] - b[i]·k], d[num][balance] + a[i]) – if we choose a fruit.
Balance can be negative, so in programming languages which don't support negative indexation, indexes should be shifted by the biggest negative number for balance. If we determine the balance as sum(b·k) - sum(a) it will be the sum of all tastes.
The answer for some path is a range under which we can go all the way, and this range is the intersection of all the ranges on the path. We can conclude it because the number is valid for path if it is valid for all ranges in the path. We will iterate all ribs. Let the left board of range on a rib is the left board of our intersection. It means we can't use ribs whith left board greater than ours. Lets iterate all right boards, determining the answer as the range from fixed left board to the chosen right. This answer exists if we have any path from the first node to the last. Let's check if the graph is connected if we leave only ribs with left board not greater than our and right board not less than our. If the graph is connected — let's update the answer. Right board can be found by binary search so the complexity is O(M2·logM).
There are many solutions for this task. I will describe my, you can deal with other by looking participants code. To find the answer we should calculate maxDis[k][k], where maxDis[i][j] – maximal complexity from note i to note j.
Now we should only iterate the song updating answer for each pair of adjacent notes. Let's think how we can calculate the matrix.
For each place (x1, y1) on the guitar let's iterate pairs (x2, y2) with y2 ≤ y1.
If (x2 ≤ x1) distance will be x1–x2 + y1–y2. So we should find minimal x2 + y2 in submatrix from (0, 0) to (x, y).
If (x2 ≥ x1) distance will be x2–x1 + y1–y2. So we should find maximal x2–y2 in submatrix from (n–1, 0) до (x, y).
We will calculate this values for each note. We need too much memory so we should memorize only one previous row for each note. For each place we will update dinamics for both variants according to already calculated and for our own note (which is in this cell) we will also compare (i + j) or (i–j) with current value in the cell.
Complexity O(N·M·K)










I (but not just me, as I noticed from looking at others' codes) have a cool solution of E:
Imagine that we want to calculate the max. distance of 2 tones a, b. Take tone a at (x1, y1) and b at (x2, y2); notice that |x1 - x2| + |y1 - y2| is the maximum of ± (x1 - x2) ± (y1 - y2) for all signs, which leads to 4 possible expressions:
Instead of limiting ourselves to the correct expression, we can evaluate the maxima of all pairs of points with all 4 expressions, and the answer will still be the maximum of them all. Notice that all 4 are linear, so we just need to calculate the maximum and minimum of $x_1+y_1$ and x1 - y1 for all points of one tone; the result for 2 tones can be found by trying the maxima of all 4 expressions, which are (in that order)
Complexity: O(NM) :D
Please elaborate the part Notice that all 4 are linear, so we just need to calculate the maximum and minimum of x1 + y1 and x1 - y1 for all points of one tone;
We compute the numbers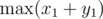 and
and 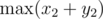 and take their difference. Similarly for the other 3 expressions, and for any pair of tones (denoted here as "1" and "2").
and take their difference. Similarly for the other 3 expressions, and for any pair of tones (denoted here as "1" and "2").
For any linear function f (UTFG if you don't know about these) we have
Actually there is a simple soluton for problem D with complexity O(M ^ 2).
Tip: Two pointers instead of binary search.
Can u double-check the expressions in solution for task C?
Can someone please explain the solution to C? I did not understand the use of balance. I just thought of doing the following: For a pair (a,b), if a/b = k, it can be.included in our solution. For all pairs for which a/b!=k, check if adding the pair to the solution satisfies given conditions. If yes, include it in solution. We can choose nC2 pairs and do the above operations in O(n^2).
I still don't understand how to handle negative indices. Btw, it's Dynamic Programming.
Yes, I got that it is dp.
the second index (
balance) always lies between-100,000and+10,000. therefore, we can access theith element of an array by shifting indices likea[i+100000](here it'sdp[i][balance+100000]), or by using other data structures like map.Oh, ok thanks!
If you sort fruits by balance in descending order, you won't need this trick with index shifting. dp[n + 1][10 * 1000] would be sufficient
I can't understand how my solution with negative array indices is able to work. Code
Can you please explain the procedure if instead of considering a[i]-k*b[i], I would have considered k*b[i]-a[i]. I am getting WA on testcase 6. https://codeforces.com/contest/366/submission/184402801
One way is to use a third state variable which denotes the sign of the difference i.e, whether the difference is +ve or -ve. Here: 45877072
In D, what do you mean by ribs and boards?
i'm not sure, but i think rib means edge, and board means bound (i.e. left board = lower bound, right board = upper bound)
can somebody explain problem D solution
I don't like how A is worded,
"If a chocolate bar for some guard costs less than the minimum chocolate bar price for this guard is, or if a box of juice for some guard costs less than the minimum box of juice price for this guard is, then the guard doesn't accept such a gift."
By using "this guard" and "some guard", it can be read that out of all the guards, this guard's minimum chocolate price must be the minimum out of every guard.
I must say problem C is amazing, never seen any problem quite like it.
dp[i+1][summation + a[i]]<<=b[i];we will shift every summation of calories by b[i];ACCEPTED
Is it doable in a recursive way? Using Bitsit.