A. Polycarp and Sums of Subsequences
The first two numbers cannot be produced by a sum operation, so we have $$$2$$$ of $$$3$$$ numbers we must find. How to find the last one? Subtract these two from the largest one.
B. Missing Bigram
We need to create an empty answer string.
Starting from the first substring, for each substring follows, if the first character of it equals the last character of the currently answer string, add the last character, otherwise, append the whole string.
In the end, check if the answer string has the length n or not. If not, repeat the last character.
Be careful of the case we didn't add any whole substring.
C. Paint the Array
The most likely answer for each case is the gcd of all odd-indexed elements or the gcd of all even-indexed elements.
Our work now is to check if it is divisible by some "neighbor index" or not.
D. Array and Operations
We need to optimize two things: the numbers we use in $$$k$$$ operations must be as large as possible, and the total result of $$$k$$$ operations must be as small as possible.
Thus, we will use $$$2k$$$ largest numbers.
E. Singers' Tour
We have a system of equations, it goes like this:
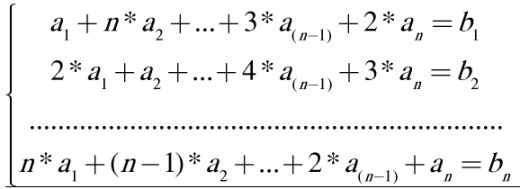
If we add all of them, we will have something like:
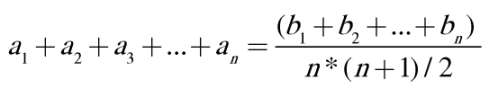
Moreover, if we subtract two neighbor equations, for example, the first from the second equation, we will get something like this:
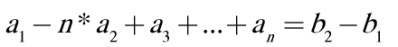
Using this we can calculate all numbers from $$$a_1$$$ to $$$a_n$$$. Of course, we will have to check the exceptions: $$$n*(n+1)/2$$$ is not divisible from the sum of all elements from $$$b$$$, or some $$$a[i]$$$ is non-positive.
F. Reverse
If $$$x = y$$$, the answer is YES.
Else if $$$y$$$ is divisible by $$$2$$$, the answer is NO.
Else we have to check if the binary string $$$s$$$ of $$$x$$$ can convert into the binary string $$$t$$$ of $$$y$$$ or not, with $$$s$$$ we can convert into several "starting strings":
Itself.
Itself, with one extra '1' at the end.
Itself but erase all '0's at the end.
Itself, erase all '0's, reversed.
Clearly, the operation is to choose to keep the string or erase all the '0's at the end then add some '1's (maybe zero) to the beginning or the end of the string.
The work now is to check each case if we can obtain $$$t$$$ by adding '1's to the beginning or the end of the current string.
G. Trader Problem
A simple way to solve: use two sets, both store vectors of four elements: the leftmost index of the segment, the rightmost index of the segment, how many numbers we take from it, and the distance between it and the next segment on the array. The first set will sort by the distance, the second set will sort by their first elements.
So how to use them? At first, merge the two arrays a and b into 1 array, let's call it TTL, use a map to save if we are currently have something or not. Then for each element, we will make a segment based on them: the leftmost and rightmost is their index, the number of elements we will take is either 1 or 0 depending on the map I described above, the distance will be the difference between it and the next number in TTL.
What will we do now? Solve the problem offline, for each query merge some of the segments which have the smallest "distance" into some other segments, so there will be no more than N merges. Since we are using sets, the complexity is O(NlogN).
To calculate the sum efficiently, use a prefix array.
Hope that my defines are not difficult to understand.
Yes, I'm a fan of neal_wu.









