The tutorial has been prepared by Fefer_Ivan and NALP.
371A - K-Periodic Array
For array to be periodic, elements 1, 1 + k, 1 + 2 * k, … must be equal. Also, elements 2, 2 + k, 2 + 2 * k, … must be equal. And so on up to k. So each element of the array is a part of exactly one group. And there are k groups total. Each such group is independent. Let’s consider some group of elements, that contain a ones and b twos. All elements in this group must be equal. So we either change all ones to twos or all twos to ones. First option will require a changing operations and second one — b changing operations. For the optimal solution, you should select the operation with smaller number of changing operations required.
371B - Fox Dividing Cheese
It is easy to see that the fox can do three type of operations: divide by 2, divide by 3 and divide by 5. Let’s write both given numbers in form a = x·2a2·3a3·5a5, b = y·2b2·3b3·5b5, where x and y are not dibisible by 2, 3 and 5. If x ≠ y the fox can’t make numbers equal and program should print -1. If x = y then soluion exists. The answer equals to |a2 - b2| + |a3 - b3| + |a5 - b5|, because |a2 - b2| is the minimal number of operations to have 2 in the same power in both numbers, |a3 - b3| is the minimal number of operations to have 3 in the same power in both numbers, and |a5 - b5| is the same for 5.
371C - Hamburgers
Let's use binary search approach. For given number of hamburgers (say, x) let's find the minimal number of money needed to cook them. Say, for one hamburger Polycarpus needs cb bread pieces, cs sausages pieces, cc cheese pieces. So for x hamburgers he needs: cb·x, cs·x and cc·x pieces (by types). Since he already has nb, ns and nc pieces, so he needs to buy:
- bread: max(0, cb·x - nb),
- sausages: max(0, cs·x - ns),
- cheese: max(0, cc·x - nc).
So the formula to calculate money to cook x hamburgers is:
Obviously, the function f(x) is monotonic (increasing). So it is possible to use binary search approach to find largest x such that f(x) ler.
371D - Vessels
The naive solution for this problem will work like this. Let us store an amount of water in each vessel in some array v. If we need to know how much water is in some vessel, we just take the number from the array. If we need to pour x units of water into vessel number i, we must follow the simple procedure: 1. If x = 0 then all water is poured and we must end the procedure 2. If i > n then all remaining water is spilled on the floor and we must end the procedure 3. If x units of water can fit into the i-th vessel, then add x to v[i] and end the procedure 4. Fill i-th vessel completely and subtract used amount from x. 5. Assign i = i + 1. 6. Go to the first step.
In the worst case scenario such procedure can iterate through all vessels each time. For example, if there are n vessels and each vessels have capacity of one unit of water, each query like 11n will take O(n) time to process.
To make this solution faster we should notice, that once completely filled, vessel can be skipped during the algorithm above because it can not consume any more water.
So instead of i = i + 1 assignment should be like i = findNextNotFilledVessel(i).
To implement this function we can use different structures. For example, we can use sorted set of numbers (set in C++, TreeSet in Java). Let store the set of indices of unfilled vessels. So to find next not filled vessel from i-th vessel, we must find smallest number, that is contained in set and is strictly greater than i. There are built-in methods for it (upper_bound in C++, higher in Java).
Also, each time we fill the vessel, we must erase corresponding index from the set.
So now we can see, that algorithm can not complete more that O((m + n)logn) operations for all queries. Because on each iteration of the pouring procedure either the vessel is filled (which can only happen n times during the whole runtime), or we run out of water (or vessels) and the procedure is stopped. So there will be only total of O(m + n) iterations of the pouring procedure and each iteration require one lookup in the sorted set, which takes O(logn) operations. So the total number of needed operations is O((m + n)logn).
371E - Subway Innovation
It is easy to see that you need to minimize the sum of pairwise distances between k stations. The main idea to do it is to sort them and the required stations will form a continuous segment. It is easy to prove by contradiction.
Huge constraints do not allow to use straight-forward method to find required segment. Let’s call f(i, k) — sum of pairwise distances of k stations starting from the i-th. To find f(0, k) you need to start from f(0, 0) = 0 and use transformation from calculated f(0, i) to f(0, i + 1). You can use equation:
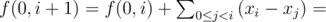
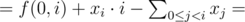
where sum(l, r) means xl + xl + 1 + ... + xr. We can precalculate sum[i] = x0 + x1 + ... + xi and use equation sum(l, r) = sum[r] - sum[l - 1] to find sum(l, r) in O(1).
Actually we need f(0, k), f(1, k) and so on (and find minimal value among them).
To recalculate f(i, k) to f(i + 1, k) you need exclude xi and include xi + k. Using the method like in the previous paragraph: f(i + 1, k) = f(i, k) - (sum(i + 1, i + k - 1) - xi·(k - 1)) + (xi + k·(k - 1) - sum(i + 1, i + k - 1)).











in 371C, i have another way to solve it. first, we use nb, ns, nc as much as possible. then, we fill the rest if there are still somethings left and it may be used. finally, use the rest of the money to buy as much as possible. the time will not over O(max(nb,ns,nc)),and they are all not over 100.
You need to be careful to that the recipe doesn't use some kind of ingredients and its initial number is not 0. If you don't notice this case will get TLE. This solution 5390433 is my first submission and it doesn't check the case i describe.
yeah, i made the same mistake in my 1st submission toooo....
For 371E, we must pay attention to using LongLong instead of Int. I got an FST because of typing Int for numbers in my stucture. I will notice that in the following contests.
For 371E I used long long and got WA on test 11. Then I changed to unsigned long long and got AC.
in 371C please can anybody explain in detail how we can use binary search in this problem
you will calculate the number of bread,cheese and sauce needed for each recipe then you will try to maximize your solution which can be affordable using binary search
BFS solution for 371B.. :) http://codeforces.com/contest/371/submission/16594018
In the question E, can’t we just find the shortest segment containing k numbers after sorting? I tried that and am getting wrong answer. What I thought was if the distance between the two ends is shortest, the pairwise sum of absolute distance of the points in between will also be minimum...
Can anyone give an example where this goes wrong?
try this n=4 1 3 5 7 n=4 1 5 6 7 Both will give different pairwise distance.
Find error if possible. https://codeforces.com/contest/371/submission/43155192
In problem B, how did he derive the forms of the two numbers?? what formula/theories he used?
We can just repeatedly divide by 2 first, then 3 and then 5 to find a2, a3, a5. If after division, both numbers aren't equal => there is no solution and you can return -1. Else, you return abs(a2 — b2) + abs(a3 — b3) + abs(a5 — b5).
Here is my code: https://codeforces.com/problemset/submission/371/52334277
I think It is not a good a good editorial. You should also give the code too. There are many people like me who needs the code as well as explanation to understand the editorial clearly. Please consider giving implementation in editorial.
If you need the code, you can view other people's submissions. Sorting by execution time can give you the most optimal ones.
But I need code that is the implementation of the idea given in Editorial. In people's submission I will not have it. Don't you think implementation should be given in editorial ?
Yeah, it would definitely be better if it was given in the editorial, but if not hopefully someone else has solved it in the same way.
For D, solution using Disjoint Sets.