Hello Codeforces!
Hello Codeforces!
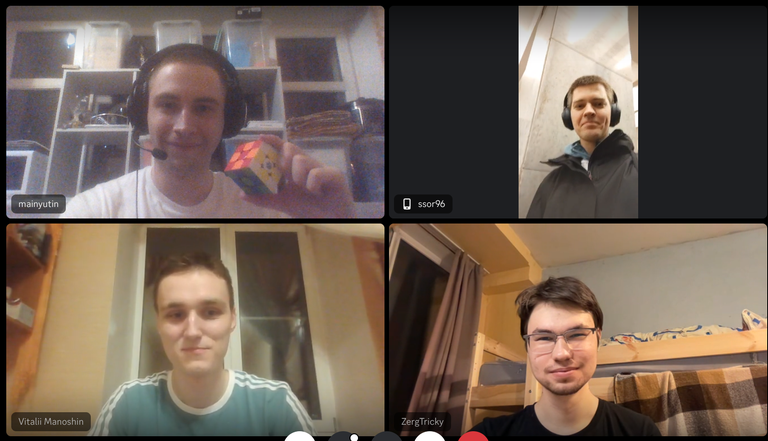
The 2023 ICPC World Finals Luxor will begin on April 18, 2024 at 10:00 UTC. This time, we have a double World Finals. You can distinguish them by colors: blue (fish emoji) and green (crocodile). Join us on the live broadcast for this awesome double event of the year in competitive programming; commentators will include ecnerwala, SecondThread, Egor, and more!
ICPC World Finals Luxor is hosted by The Arab Academy for Science, Technology, & Maritime Transport (AASTMT), the ICPC World Finalist teams for two seasons will compete for World Championship awards, prizes, and bragging rights. More than 130 teams of each season represent the best of great universities of eight ICPC regions.
Some useful links:
- Official website of the ICPC
- Official ICPC WF Luxor website
- Schedule of Events
- Live broadcast
- Photo Gallery
- Mirrow Contest
- ICPC World Finals Mirror (ksun48 + Petr + tourist)
- Luxor brochure
Scoreboards:
All available broadcasts:
Also, you can observe teams' monitors and web cameras on the separate broadcast. Sent team's hashtag to the chat to see your favorite! All hashtags for both seasons were collected in this list
We wish good luck to all competing teams to have a great time spending, and to do the best to get amazing results!